

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Производная по направлению и градиент
Похожие статьи вашей тематики
Пусть точка  входит (вместе с некоторой окрестностью) в область определения функции двух переменных входит (вместе с некоторой окрестностью) в область определения функции двух переменных  . Пусть значение функции в этой точке равно некоторому числу . Пусть значение функции в этой точке равно некоторому числу  : :  . Переместимся теперь из этой точки на одно и то же (небольшое – чтобы не выйти за область определения функции) расстояние, но по разным направлениям. Мы попадем в некоторые другие точки области определения данной функции (см. рисунок). Если теперь вычислить значения функции в получившихся точках, то можно заметить, что значения функции в них окажутся в общем случае разными, несмотря на то, что сдвигались от начальной точки на одно и то же расстояние. Для некоторых точек значения функции в них увеличились (по сравнению с числом . Переместимся теперь из этой точки на одно и то же (небольшое – чтобы не выйти за область определения функции) расстояние, но по разным направлениям. Мы попадем в некоторые другие точки области определения данной функции (см. рисунок). Если теперь вычислить значения функции в получившихся точках, то можно заметить, что значения функции в них окажутся в общем случае разными, несмотря на то, что сдвигались от начальной точки на одно и то же расстояние. Для некоторых точек значения функции в них увеличились (по сравнению с числом  ), а для некоторых уменьшились. Для некоторых увеличились больше, для других меньше и т.д.. Таким образом, характер и скорость изменения функции при смещении из данной точки зависит не только от величины сдвига, но и от его направления. Для функции одного переменного вводилось понятие производной, которая как раз и характеризовала характер и скорость изменения функции в данной точке. Для функции двух (и более – тем более!) переменных кроме задания исходной точки ), а для некоторых уменьшились. Для некоторых увеличились больше, для других меньше и т.д.. Таким образом, характер и скорость изменения функции при смещении из данной точки зависит не только от величины сдвига, но и от его направления. Для функции одного переменного вводилось понятие производной, которая как раз и характеризовала характер и скорость изменения функции в данной точке. Для функции двух (и более – тем более!) переменных кроме задания исходной точки  для характеристики изменения функции необходимо (как выяснилось) задать и направление смещения – по разным направлениям характер изменения функции разный. Поэтому и вводится понятие производной функции двух переменных в заданной точке по заданному направлению, которое характеризует характер и скорость изменения функции в этом направлении. Положение точки для характеристики изменения функции необходимо (как выяснилось) задать и направление смещения – по разным направлениям характер изменения функции разный. Поэтому и вводится понятие производной функции двух переменных в заданной точке по заданному направлению, которое характеризует характер и скорость изменения функции в этом направлении. Положение точки  определяется, понятно, заданием ее координат определяется, понятно, заданием ее координат 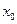 и и  . Обозначим какое-либо выходящее из точки . Обозначим какое-либо выходящее из точки  направление буквой, например, буквой направление буквой, например, буквой  . Каким объектом можно однозначно задать направление . Каким объектом можно однозначно задать направление  ? Направление проще всего задавать вектором. Поскольку длина этого вектора не имеет значения (а только его направление), то будем считать, что направление ? Направление проще всего задавать вектором. Поскольку длина этого вектора не имеет значения (а только его направление), то будем считать, что направление  движения из данной точки движения из данной точки  характеризуется вектором характеризуется вектором   длины 1 (т.е. длины 1 (т.е.  ), имеющем направление ), имеющем направление  . Фактически координаты . Фактически координаты  и и 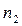 вектора вектора  − это направляющие косинусы вектора − это направляющие косинусы вектора  , расположенного в координатной плоскости хОу (проходили такие в теме «Векторы» − это косинусы углов, которые составляет данный вектор , расположенного в координатной плоскости хОу (проходили такие в теме «Векторы» − это косинусы углов, которые составляет данный вектор  с осями Ох и Оу, если сам вектор отложить от начала координат − см. рисунок): с осями Ох и Оу, если сам вектор отложить от начала координат − см. рисунок):  , ,  . Ясно, что угол . Ясно, что угол  вполне определяется углом вполне определяется углом  , отсчитываемом от оси , отсчитываемом от оси  до вектора до вектора  против часовой стрелки. Например, если угол против часовой стрелки. Например, если угол  − острый, то ясно из рисунка, что углы − острый, то ясно из рисунка, что углы  и и  в сумме составляют 90 в сумме составляют 90  , а потому , а потому  . А тогда, вспоминая формулы приведения в тригонометрии, получаем . А тогда, вспоминая формулы приведения в тригонометрии, получаем  . Таким образом, координаты . Таким образом, координаты  и и 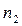 вектора вектора  можно выразить только через один угол − угол можно выразить только через один угол − угол  , который вектор , который вектор  составляет с осью х: составляет с осью х:
(1) 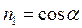 , ,  . .
Не вдаваясь в подробности, можно сказать, что для функции двух переменных  производная в точке производная в точке  по направлению по направлению  определяется (по аналогии с понятием обычной производной для функции определяется (по аналогии с понятием обычной производной для функции  одного переменного) как предел отношения приращения функции к величине сдвига в направлении одного переменного) как предел отношения приращения функции к величине сдвига в направлении  из исходной точки из исходной точки  , когда величина этого сдвига стремиться к 0. После некоторых преобразований этого предела возникает определенная формула для его вычисления, которую мы и примем в качестве конструктивного определения производной по направлению. Производной функции , когда величина этого сдвига стремиться к 0. После некоторых преобразований этого предела возникает определенная формула для его вычисления, которую мы и примем в качестве конструктивного определения производной по направлению. Производной функции  в точке в точке  по направлению по направлению  , задаваемому единичным вектором , задаваемому единичным вектором  , называется число, обозначаемое , называется число, обозначаемое  , и вычисляемое по формуле , и вычисляемое по формуле
(2) 
Эта производная определяет характер и скорость изменения функции из данной точки по заданному направлению. Если такая производная оказалась положительной, то функция из данной точки в данном направлении возрастает (и чем больше производная – тем быстрее), а если отрицательной – то убывает.
Если направление  для производной задано произвольным (не обязательно длины 1) вектором для производной задано произвольным (не обязательно длины 1) вектором  , то координаты единичного вектора , то координаты единичного вектора  вдоль этого направления находятся по формулам вычисления направляющих косинусов (были в той же теме «Векторы»): вдоль этого направления находятся по формулам вычисления направляющих косинусов (были в той же теме «Векторы»):
(3)  , ,  , ,
где 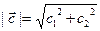 – длина вектора – длина вектора  . Если же направление . Если же направление  задано углом задано углом  , который составляет данное направление с осью х (отсчитывается от оси х против часовой стрелки), то координаты единичного вектора , который составляет данное направление с осью х (отсчитывается от оси х против часовой стрелки), то координаты единичного вектора  вычисляются, согласно (1), по формулам вычисляются, согласно (1), по формулам  , ,  . .
Из сказанного выводится следующая схема вычисления производной функции  в точке в точке  по заданному направлению по заданному направлению  : :
· Находим выражения для частных производных  и и  . .
· Находим значения  и и  этих производных в заданной точке этих производных в заданной точке  , подставляя , подставляя  и и  в полученные выражения для в полученные выражения для  и и  . .
· Находим координаты 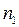 и и  единичного вектора единичного вектора  заданного направления заданного направления  . Если направление задано вектором . Если направление задано вектором  , то используем формулы (3), а если направление задается его углом , то используем формулы (3), а если направление задается его углом  с осью с осью  , то формулы (1). , то формулы (1).
· Вычисляем производную по формуле (2).
Пример 1. Найти производную функции  в точке в точке  по направлению вектора по направлению вектора  , где , где  . .
Решение. Вычисления ведем по приведенной выше схеме. Находим частные производные:  , ,  . Далее, находим значения вычисленных производных в точке . Далее, находим значения вычисленных производных в точке  : :  , ,  . По условию задачи направление дифференцирования . По условию задачи направление дифференцирования  задано вектором задано вектором 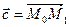 с известными координатами начальной с известными координатами начальной  и конечной точки и конечной точки  . Находим координаты этого вектора, вычитая из координат конечной его точки координаты начальной точки: . Находим координаты этого вектора, вычитая из координат конечной его точки координаты начальной точки:  . Теперь по формулам (3) найдем координаты . Теперь по формулам (3) найдем координаты 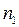 и и  единичного вектора единичного вектора  вдоль заданного направления: вдоль заданного направления:  , ,  , ,   . Наконец, по формулам (2) находим искомую производную: . Наконец, по формулам (2) находим искомую производную:  . .
Пример 2. Найти производную функции  в точке в точке  по направлению, образующему угол по направлению, образующему угол  с осью х. с осью х.
Решение. В предыдущем примере уже найдены частные производные этой функции в нужной нам точке (функция и точка – те же самые):  , ,  . Поскольку направление . Поскольку направление  задается углом задается углом  этого направления с осью этого направления с осью  , то по формулам (1) находим координаты единичного вектора , то по формулам (1) находим координаты единичного вектора  по направлению по направлению  : :  , ,  . Теперь по формуле (2) получаем . Теперь по формуле (2) получаем  . .
Сделаем некоторые выводы по примерам 1 и 2. В них требовалось найти производную от одной и той же функции  в одной и той же точке в одной и той же точке  , но в разных направлениях. Поскольку в каждом примере производные получились положительными, то можно сделать вывод, что по каждому направлению функция из данной точки возрастает. Но все-таки производная по второму направлению, равная , но в разных направлениях. Поскольку в каждом примере производные получились положительными, то можно сделать вывод, что по каждому направлению функция из данной точки возрастает. Но все-таки производная по второму направлению, равная  , больше производной по первому направлению, равной , больше производной по первому направлению, равной  . Поэтому по второму направлению функция из данной точки возрастает быстрее, чем по первому. . Поэтому по второму направлению функция из данной точки возрастает быстрее, чем по первому.
Во многих практических задачах возникает необходимость найти направление из данной точки, по которому функция возрастает быстрее всего. Другими словами, необходимо найти направление, производная по которому из данной точки максимальна. Оказывается, что это направление наискорейшего возрастания функции из данной точки определяется вектором, координаты которого совпадают со значениями частных производных в данной точке и который называется градиентом данной функции в данной точке. Итак, градиентом функции  в точке в точке  называется вектор с координатами называется вектор с координатами  и и  . Обозначение градиента: . Обозначение градиента:   или или 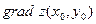 . Как уже было сказано, вектор-градиент . Как уже было сказано, вектор-градиент
(4) 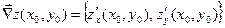
показывает направление наискорейшего возрастания функции из данной точки. Производная по этому направлению максимальна и численно равна длине вектора градиента  . .
Пример 3. Найти градиент функции  в точке в точке  и вычислить производную в направлении градиента. и вычислить производную в направлении градиента.
Решение. В предыдущем примере 1 уже были найдены частные производные этой функции в нужной нам точке (функция и точка – те же самые):  , ,  . Тогда по формуле (4) градиент есть вектор с координатами 6 и 4: . Тогда по формуле (4) градиент есть вектор с координатами 6 и 4:  . Величина производной в направлении . Величина производной в направлении  этого вектора равна, как сказано выше, модулю градиента, т.е. этого вектора равна, как сказано выше, модулю градиента, т.е.  . Как и следовало ожидать (производная в направлении градиента – максимальна!), эта производная больше, чем производная по направлениям, задаваемым в примерах 1 и 2. . Как и следовало ожидать (производная в направлении градиента – максимальна!), эта производная больше, чем производная по направлениям, задаваемым в примерах 1 и 2.
А теперь приведем более сложный пример применения градиента в задаче с практическим содержанием.
Пример 4. Прибыль некоторого предприятия Y характеризуется так называемой производственной функцией Кобба-Дугласа двух переменных вида  , где , где  – затраты на капитал, – затраты на капитал,  – затраты на труд. Начальные объемы вложенных в производство средств таковы: – затраты на труд. Начальные объемы вложенных в производство средств таковы:  у.е., а у.е., а  у.е.. Появилась дополнительная возможность вложить в производство 16 у.е.. Как следует наилучшим образом распределить эти средства между капиталом у.е.. Появилась дополнительная возможность вложить в производство 16 у.е.. Как следует наилучшим образом распределить эти средства между капиталом  и трудом и трудом  , чтобы эффект вложения был максимальный? , чтобы эффект вложения был максимальный?
Решение. В данном примере вместо привычного обозначения переменных  , ,   и и  для функции двух переменных для функции двух переменных  используются переменные, обозначенные используются переменные, обозначенные  , ,   и и  (для функции (для функции  ), так как эти обозначения традиционно приняты в экономической теории. Вычислим сначала доход производства (обозначим его ), так как эти обозначения традиционно приняты в экономической теории. Вычислим сначала доход производства (обозначим его  ) при первоначальном распределении средств. Для этого необходимо посчитать значение функции ) при первоначальном распределении средств. Для этого необходимо посчитать значение функции  при при  и и  , т.е. вычислить значение этой функции в точке , т.е. вычислить значение этой функции в точке  : :  . Итак, первоначальный доход составлял 80 у.е.. Допустим, что мы распределили дополнительные средства в 16 у.е. между капиталом и трудом следующим образом: к первоначальным капитальным затратам мы добавили . Итак, первоначальный доход составлял 80 у.е.. Допустим, что мы распределили дополнительные средства в 16 у.е. между капиталом и трудом следующим образом: к первоначальным капитальным затратам мы добавили 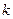 у.е. (т.е. стало у.е. (т.е. стало  у.е.), а к трудовым затратам добавили у.е.), а к трудовым затратам добавили  у.е. (стало у.е. (стало  у.е.). Числами у.е.). Числами 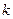 и и  мы можем распоряжаться сами, но так, чтобы, конечно, выполнялось условие, что мы можем распоряжаться сами, но так, чтобы, конечно, выполнялось условие, что  . Как же выбрать эти числа наилучшим образом? Наилучший выбор, очевидно, тот, при котором получаемая прибыль (т.е. значение функции . Как же выбрать эти числа наилучшим образом? Наилучший выбор, очевидно, тот, при котором получаемая прибыль (т.е. значение функции  ) будет максимальной. Такая задача может быть решена точно сведением ее к задаче отыскания наибольшего значения непрерывной функции одного переменного на отрезке (решение таких задач ранее разбиралось). Но мы исследуем эту задачу с помощью введенного нами понятия градиента, которое позволит нам получить хоть и не точное, но достаточно хорошее приближенное решение. ) будет максимальной. Такая задача может быть решена точно сведением ее к задаче отыскания наибольшего значения непрерывной функции одного переменного на отрезке (решение таких задач ранее разбиралось). Но мы исследуем эту задачу с помощью введенного нами понятия градиента, которое позволит нам получить хоть и не точное, но достаточно хорошее приближенное решение.
После указанного распределения добавочных средств величина прибыли (обозначим ее  ) есть значение функции ) есть значение функции  в новой точке в новой точке  : :  . Таким образом, мы хотим изучить изменение функции . Таким образом, мы хотим изучить изменение функции  при перемещении из точки при перемещении из точки  в точку в точку 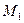 , т.е. изменении функции из точки , т.е. изменении функции из точки  в направлении вектора в направлении вектора  . При различном выборе . При различном выборе 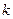 и и  будет меняться положение точки будет меняться положение точки  , а потому будет меняться и направление , а потому будет меняться и направление  изменения функции. Нам нужно, чтобы прибыль от вложения дополнительных средств была максимальной, т.е. чтобы в направлении изменения функции. Нам нужно, чтобы прибыль от вложения дополнительных средств была максимальной, т.е. чтобы в направлении  функция прибыли функция прибыли  возрастала бы быстрее всего. Но мы уже знаем, что наибыстрейшее возрастание функции обеспечивает движение по направлению вектора градиента в точке возрастала бы быстрее всего. Но мы уже знаем, что наибыстрейшее возрастание функции обеспечивает движение по направлению вектора градиента в точке  , т.е. вектора , т.е. вектора  . Таким образом, наилучший выбор будет тогда, когда векторы . Таким образом, наилучший выбор будет тогда, когда векторы  и и  задают одно и то же направление из точки задают одно и то же направление из точки  . Это будет только в том случае, если векторы параллельны (точнее, сонаправлены). Таким образом, оптимальные значения . Это будет только в том случае, если векторы параллельны (точнее, сонаправлены). Таким образом, оптимальные значения 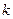 и и  должны удовлетворять двум условиям: должны удовлетворять двум условиям:
(5)  , ,    ( ( ). ).
В приведенном рассуждении я незаметно несколько слукавил, а потому в результате мы получим, как я предупреждал, не точное, а приближенное решение. Найдем координаты вектора  по известным координатам его начальной и конечной точек: по известным координатам его начальной и конечной точек:  , т.е. , т.е.  . Найдем координаты вектора . Найдем координаты вектора 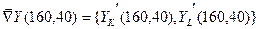 . Находим частные производные: . Находим частные производные:    ; аналогично получаем производную по ; аналогично получаем производную по  : :  . Тогда . Тогда  , , 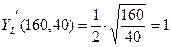 , а потому , а потому  . Как известно из аналитической геометрии, векторы параллельны в том случае, если их координаты пропорциональны (т.е. отношение их первых координат векторов равно отношению вторых). Поэтому . Как известно из аналитической геометрии, векторы параллельны в том случае, если их координаты пропорциональны (т.е. отношение их первых координат векторов равно отношению вторых). Поэтому    только в том случае, если выполнено: только в том случае, если выполнено:  , т.е. , т.е. 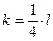 или или  . Таким образом, из (5) следует, что оптимальные значения . Таким образом, из (5) следует, что оптимальные значения 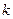 и и  удовлетворяют системе уравнений: удовлетворяют системе уравнений:  . Подставляя . Подставляя  из второго уравнения в первой, найдем из второго уравнения в первой, найдем  , а тогда , а тогда  . Итак, оптимальным будет такое распределение дополнительных средств: капитальные затраты увеличить на 3.2 у.е., а трудовые – на 12.8 у.е.. При этом новые капитальные и трудовые затраты составят . Итак, оптимальным будет такое распределение дополнительных средств: капитальные затраты увеличить на 3.2 у.е., а трудовые – на 12.8 у.е.. При этом новые капитальные и трудовые затраты составят 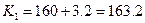 и и  у.е., а прибыль станет у.е., а прибыль станет  у.е.. Как мы видим, значительную долю дополнительных средств рекомендуется вложить в трудовые ресурсы и лишь незначительную – на капитальные затраты. Отметим, что точное решение этой задачи (о возможности получения которого говорилось выше) рекомендует вообще все дополнительные средства вложить только в трудовые ресурсы. При этом прибыль станет равной у.е.. Как мы видим, значительную долю дополнительных средств рекомендуется вложить в трудовые ресурсы и лишь незначительную – на капитальные затраты. Отметим, что точное решение этой задачи (о возможности получения которого говорилось выше) рекомендует вообще все дополнительные средства вложить только в трудовые ресурсы. При этом прибыль станет равной 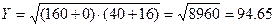 у.е.. у.е..
 Теперь по аналогии с изложенным выше для функции двух переменных введем понятия производной по направлению и градиента для функций трех (и более) переменных. Пусть точка Теперь по аналогии с изложенным выше для функции двух переменных введем понятия производной по направлению и градиента для функций трех (и более) переменных. Пусть точка  входит (вместе с некоторой окрестностью) в область определения функции входит (вместе с некоторой окрестностью) в область определения функции  трех переменных (теперь эта область уже некоторая объемная фигура в пространстве). Пусть значение функции в этой точке равно некоторому числу трех переменных (теперь эта область уже некоторая объемная фигура в пространстве). Пусть значение функции в этой точке равно некоторому числу  : :  . Перемещаясь из этой точки по разным направлениям в пространстве мы опять будем наблюдать различный характер изменения значений функции в зависимости от направления. Как и в случае функций двух переменных, определенное направление в пространстве обозначим буквой . Перемещаясь из этой точки по разным направлениям в пространстве мы опять будем наблюдать различный характер изменения значений функции в зависимости от направления. Как и в случае функций двух переменных, определенное направление в пространстве обозначим буквой  и будем задавать его вектором и будем задавать его вектором 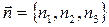 длины 1 (т.е. длины 1 (т.е. 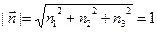 ). Координаты ). Координаты  , , 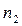 и и  вектора вектора  − это направляющие косинусы вектора − это направляющие косинусы вектора  в пространстве, т.е. косинусы углов, которые составляет данный вектор в пространстве, т.е. косинусы углов, которые составляет данный вектор  с осями координат, если сам вектор отложить от начала координат (см. рисунок): с осями координат, если сам вектор отложить от начала координат (см. рисунок):
(6)  , ,  , ,  . .
По аналогии вводим определение производной по направлению для функции трех переменных. Производной функции  в точке в точке  по направлению по направлению  , задаваемому единичным вектором , задаваемому единичным вектором 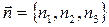 , называется число, обозначаемое , называется число, обозначаемое  , и вычисляемое по формуле , и вычисляемое по формуле
(7)  . .
Точно так же, как и в случае функции двух переменных, если направление  для производной задано произвольным (не обязательно длины 1) вектором для производной задано произвольным (не обязательно длины 1) вектором  в пространстве, то координаты единичного вектора в пространстве, то координаты единичного вектора 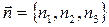 вдоль заданного направления находятся по формулам вычисления направляющих косинусов: вдоль заданного направления находятся по формулам вычисления направляющих косинусов:
(8)  , ,  , ,  . .
Поэтому получается аналогичная схема вычисления производной функции трех переменных  в точке в точке  по заданному направлению по заданному направлению  : :
· Находим выражения для частных производных  , ,  и и  . .
· Находим значения  , ,  и и  этих производных в заданной точке этих производных в заданной точке  . .
· Находим координаты 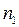 , ,  и и  единичного вектора единичного вектора  вдоль заданного направления вдоль заданного направления  (по формулам (8) либо из других соображений). (по формулам (8) либо из других соображений).
· Вычисляем производную по формуле (7).
Пример 5. Найти производную функции  в точке в точке  по направлению вектора по направлению вектора  . .
Решение. Вычисления ведем по приведенной выше схеме. Находим частные производные:  , ,  {в первом слагаемом нет {в первом слагаемом нет  } } 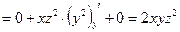 , ,
 . .
Далее, находим значения вычисленных производных в точке  : :  , ,  , ,  . По условию задачи направление . По условию задачи направление  задано вектором задано вектором  , длина которого , длина которого  . По формулам (8) найдем координаты единичного вектора . По формулам (8) найдем координаты единичного вектора  вдоль заданного направления вдоль заданного направления  : :  , , 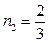 , ,  . Наконец, по формуле (7) находим искомую производную: . Наконец, по формуле (7) находим искомую производную:  . То, что ее значение оказалось отрицательным, говорит о том, что функция в этом направлении из данной точки убывает. . То, что ее значение оказалось отрицательным, говорит о том, что функция в этом направлении из данной точки убывает.
Аналогично вводится и понятие градиента функции трех (и более) переменных в связи с поиском направления наискорейшего возрастания функции их данной точки. Г радиентом функции  в точке в точке  называется вектор с координатами называется вектор с координатами  , ,  и и  . Обозначение градиента: . Обозначение градиента:   или или  . Таким образом, . Таким образом,
(9)  . .
Как и в случае функции двух переменных, направление, задаваемое этим вектором, является направлением наискорейшего возрастания функции  из данной точки из данной точки  . Производная по этому направлению максимальна и численно равна длине вектора градиента . Производная по этому направлению максимальна и численно равна длине вектора градиента  . .
Пример 6. Найти направление наискорейшего возрастания (т.е. градиент) функции  в точке в точке  и вычислить производную в этом направлении. и вычислить производную в этом направлении.
Решение. В предыдущем примере 5 уже были найдены частные производные этой функции в нужной нам точке (функция и точка – те же самые):  , ,  , ,  . Тогда по формуле (9): . Тогда по формуле (9): 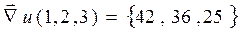 . Направление . Направление  , определяемое этим вектором, и будет направлением наискорейшего возрастания. Величина производной в направлении , определяемое этим вектором, и будет направлением наискорейшего возрастания. Величина производной в направлении  равна, как сказано выше, модулю градиента, т.е. равна, как сказано выше, модулю градиента, т.е.  . .
|



 входит (вместе с некоторой окрестностью) в область определения функции двух переменных
входит (вместе с некоторой окрестностью) в область определения функции двух переменных  . Пусть значение функции в этой точке равно некоторому числу
. Пусть значение функции в этой точке равно некоторому числу  :
:  . Переместимся теперь из этой точки на одно и то же (небольшое – чтобы не выйти за область определения функции) расстояние, но по разным направлениям. Мы попадем в некоторые другие точки области определения данной функции (см. рисунок). Если теперь вычислить значения функции в получившихся точках, то можно заметить, что значения функции в них окажутся в общем случае разными, несмотря на то, что сдвигались от начальной точки на одно и то же расстояние. Для некоторых точек значения функции в них увеличились (по сравнению с числом
. Переместимся теперь из этой точки на одно и то же (небольшое – чтобы не выйти за область определения функции) расстояние, но по разным направлениям. Мы попадем в некоторые другие точки области определения данной функции (см. рисунок). Если теперь вычислить значения функции в получившихся точках, то можно заметить, что значения функции в них окажутся в общем случае разными, несмотря на то, что сдвигались от начальной точки на одно и то же расстояние. Для некоторых точек значения функции в них увеличились (по сравнению с числом  ), а для некоторых уменьшились. Для некоторых увеличились больше, для других меньше и т.д.. Таким образом, характер и скорость изменения функции при смещении из данной точки зависит не только от величины сдвига, но и от его направления. Для функции одного переменного вводилось понятие производной, которая как раз и характеризовала характер и скорость изменения функции в данной точке. Для функции двух (и более – тем более!) переменных кроме задания исходной точки
), а для некоторых уменьшились. Для некоторых увеличились больше, для других меньше и т.д.. Таким образом, характер и скорость изменения функции при смещении из данной точки зависит не только от величины сдвига, но и от его направления. Для функции одного переменного вводилось понятие производной, которая как раз и характеризовала характер и скорость изменения функции в данной точке. Для функции двух (и более – тем более!) переменных кроме задания исходной точки 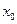 и
и  . Обозначим какое-либо выходящее из точки
. Обозначим какое-либо выходящее из точки  . Каким объектом можно однозначно задать направление
. Каким объектом можно однозначно задать направление 
 длины 1 (т.е.
длины 1 (т.е.  ), имеющем направление
), имеющем направление  и
и 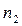 вектора
вектора  − это направляющие косинусы вектора
− это направляющие косинусы вектора  ,
,  . Ясно, что угол
. Ясно, что угол  вполне определяется углом
вполне определяется углом  , отсчитываемом от оси
, отсчитываемом от оси  до вектора
до вектора  , а потому
, а потому  . А тогда, вспоминая формулы приведения в тригонометрии, получаем
. А тогда, вспоминая формулы приведения в тригонометрии, получаем  . Таким образом, координаты
. Таким образом, координаты 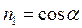 ,
,  .
. одного переменного) как предел отношения приращения функции к величине сдвига в направлении
одного переменного) как предел отношения приращения функции к величине сдвига в направлении  , и вычисляемое по формуле
, и вычисляемое по формуле
 , то координаты единичного вектора
, то координаты единичного вектора  ,
,  ,
,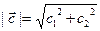 – длина вектора
– длина вектора  . Если же направление
. Если же направление  ,
,  .
. и
и  .
. и
и  этих производных в заданной точке
этих производных в заданной точке  и
и  в полученные выражения для
в полученные выражения для 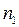 и
и  единичного вектора
единичного вектора  заданного направления
заданного направления  , то формулы (1).
, то формулы (1). в точке
в точке  по направлению вектора
по направлению вектора  , где
, где  .
. ,
,  . Далее, находим значения вычисленных производных в точке
. Далее, находим значения вычисленных производных в точке  ,
,  . По условию задачи направление дифференцирования
. По условию задачи направление дифференцирования 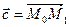 с известными координатами начальной
с известными координатами начальной  . Теперь по формулам (3) найдем координаты
. Теперь по формулам (3) найдем координаты  ,
,  ,
, 
 . Наконец, по формулам (2) находим искомую производную:
. Наконец, по формулам (2) находим искомую производную:  .
. с осью х.
с осью х. ,
,  . Поскольку направление
. Поскольку направление  этого направления с осью
этого направления с осью  ,
,  . Теперь по формуле (2) получаем
. Теперь по формуле (2) получаем  .
. , больше производной по первому направлению, равной
, больше производной по первому направлению, равной  . Поэтому по второму направлению функция из данной точки возрастает быстрее, чем по первому.
. Поэтому по второму направлению функция из данной точки возрастает быстрее, чем по первому. и
и  . Обозначение градиента:
. Обозначение градиента: 
 или
или 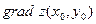 . Как уже было сказано, вектор-градиент
. Как уже было сказано, вектор-градиент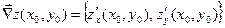
 .
. . Величина производной в направлении
. Величина производной в направлении  . Как и следовало ожидать (производная в направлении градиента – максимальна!), эта производная больше, чем производная по направлениям, задаваемым в примерах 1 и 2.
. Как и следовало ожидать (производная в направлении градиента – максимальна!), эта производная больше, чем производная по направлениям, задаваемым в примерах 1 и 2. , где
, где  – затраты на капитал,
– затраты на капитал,  – затраты на труд. Начальные объемы вложенных в производство средств таковы:
– затраты на труд. Начальные объемы вложенных в производство средств таковы:  у.е., а
у.е., а  у.е.. Появилась дополнительная возможность вложить в производство 16 у.е.. Как следует наилучшим образом распределить эти средства между капиталом
у.е.. Появилась дополнительная возможность вложить в производство 16 у.е.. Как следует наилучшим образом распределить эти средства между капиталом  ,
,  для функции двух переменных
для функции двух переменных  используются переменные, обозначенные
используются переменные, обозначенные  ,
,  ) при первоначальном распределении средств. Для этого необходимо посчитать значение функции
) при первоначальном распределении средств. Для этого необходимо посчитать значение функции  и
и  , т.е. вычислить значение этой функции в точке
, т.е. вычислить значение этой функции в точке  :
:  . Итак, первоначальный доход составлял 80 у.е.. Допустим, что мы распределили дополнительные средства в 16 у.е. между капиталом и трудом следующим образом: к первоначальным капитальным затратам мы добавили
. Итак, первоначальный доход составлял 80 у.е.. Допустим, что мы распределили дополнительные средства в 16 у.е. между капиталом и трудом следующим образом: к первоначальным капитальным затратам мы добавили 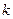 у.е. (т.е. стало
у.е. (т.е. стало  у.е.), а к трудовым затратам добавили
у.е.), а к трудовым затратам добавили  у.е.). Числами
у.е.). Числами  . Как же выбрать эти числа наилучшим образом? Наилучший выбор, очевидно, тот, при котором получаемая прибыль (т.е. значение функции
. Как же выбрать эти числа наилучшим образом? Наилучший выбор, очевидно, тот, при котором получаемая прибыль (т.е. значение функции  ) есть значение функции
) есть значение функции  :
:  . Таким образом, мы хотим изучить изменение функции
. Таким образом, мы хотим изучить изменение функции  в точку
в точку 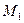 , т.е. изменении функции из точки
, т.е. изменении функции из точки  . При различном выборе
. При различном выборе  , а потому будет меняться и направление
, а потому будет меняться и направление  . Таким образом, наилучший выбор будет тогда, когда векторы
. Таким образом, наилучший выбор будет тогда, когда векторы 
 ).
). , т.е.
, т.е.  . Найдем координаты вектора
. Найдем координаты вектора 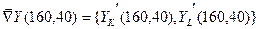 . Находим частные производные:
. Находим частные производные: 

 ; аналогично получаем производную по
; аналогично получаем производную по  . Тогда
. Тогда  ,
, 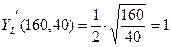 , а потому
, а потому  . Как известно из аналитической геометрии, векторы параллельны в том случае, если их координаты пропорциональны (т.е. отношение их первых координат векторов равно отношению вторых). Поэтому
. Как известно из аналитической геометрии, векторы параллельны в том случае, если их координаты пропорциональны (т.е. отношение их первых координат векторов равно отношению вторых). Поэтому  , т.е.
, т.е. 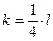 или
или  . Таким образом, из (5) следует, что оптимальные значения
. Таким образом, из (5) следует, что оптимальные значения  . Подставляя
. Подставляя  , а тогда
, а тогда  . Итак, оптимальным будет такое распределение дополнительных средств: капитальные затраты увеличить на 3.2 у.е., а трудовые – на 12.8 у.е.. При этом новые капитальные и трудовые затраты составят
. Итак, оптимальным будет такое распределение дополнительных средств: капитальные затраты увеличить на 3.2 у.е., а трудовые – на 12.8 у.е.. При этом новые капитальные и трудовые затраты составят 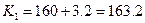 и
и  у.е., а прибыль станет
у.е., а прибыль станет  у.е.. Как мы видим, значительную долю дополнительных средств рекомендуется вложить в трудовые ресурсы и лишь незначительную – на капитальные затраты. Отметим, что точное решение этой задачи (о возможности получения которого говорилось выше) рекомендует вообще все дополнительные средства вложить только в трудовые ресурсы. При этом прибыль станет равной
у.е.. Как мы видим, значительную долю дополнительных средств рекомендуется вложить в трудовые ресурсы и лишь незначительную – на капитальные затраты. Отметим, что точное решение этой задачи (о возможности получения которого говорилось выше) рекомендует вообще все дополнительные средства вложить только в трудовые ресурсы. При этом прибыль станет равной 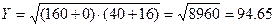 у.е..
у.е.. Теперь по аналогии с изложенным выше для функции двух переменных введем понятия производной по направлению и градиента для функций трех (и более) переменных. Пусть точка
Теперь по аналогии с изложенным выше для функции двух переменных введем понятия производной по направлению и градиента для функций трех (и более) переменных. Пусть точка  входит (вместе с некоторой окрестностью) в область определения функции
входит (вместе с некоторой окрестностью) в область определения функции  трех переменных (теперь эта область уже некоторая объемная фигура в пространстве). Пусть значение функции в этой точке равно некоторому числу
трех переменных (теперь эта область уже некоторая объемная фигура в пространстве). Пусть значение функции в этой точке равно некоторому числу  :
:  . Перемещаясь из этой точки по разным направлениям в пространстве мы опять будем наблюдать различный характер изменения значений функции в зависимости от направления. Как и в случае функций двух переменных, определенное направление в пространстве обозначим буквой
. Перемещаясь из этой точки по разным направлениям в пространстве мы опять будем наблюдать различный характер изменения значений функции в зависимости от направления. Как и в случае функций двух переменных, определенное направление в пространстве обозначим буквой 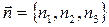 длины 1 (т.е.
длины 1 (т.е. 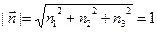 ). Координаты
). Координаты  вектора
вектора  ,
,  ,
,  .
. , и вычисляемое по формуле
, и вычисляемое по формуле .
. в пространстве, то координаты единичного вектора
в пространстве, то координаты единичного вектора  ,
,  .
. ,
,  и
и  .
. ,
,  и
и  этих производных в заданной точке
этих производных в заданной точке  единичного вектора
единичного вектора  в точке
в точке  по направлению вектора
по направлению вектора  .
. ,
,  {в первом слагаемом нет
{в первом слагаемом нет 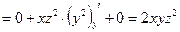 ,
, .
. ,
,  ,
,  . По условию задачи направление
. По условию задачи направление  . По формулам (8) найдем координаты единичного вектора
. По формулам (8) найдем координаты единичного вектора  ,
, 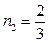 ,
,  . Наконец, по формуле (7) находим искомую производную:
. Наконец, по формуле (7) находим искомую производную:  . То, что ее значение оказалось отрицательным, говорит о том, что функция в этом направлении из данной точки убывает.
. То, что ее значение оказалось отрицательным, говорит о том, что функция в этом направлении из данной точки убывает. ,
,  и
и  . Обозначение градиента:
. Обозначение градиента:  или
или  . Таким образом,
. Таким образом, .
. .
. ,
,  ,
,  . Тогда по формуле (9):
. Тогда по формуле (9): 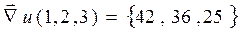 . Направление
. Направление  .
.


