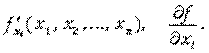Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцируемость Ф.Н.П. Частные производные. ДифференциалСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дифференцируемость Ф.Н.П. Частные производные. Дифференциал Дифференцирование сложной Ф.Н.П. неявной Ф.Н.П. Градиент, производная по направлению ФНП, касательные плоскости Частные производные и дифференциалы высшего порядка Формула Тейлора для ФНП Экстремум ФНП. Необходимое условие экстремума ФНП Достаточное условие экстремума ФНП, критерий Сильвестра Условный экстремум ФНП. Метод множителей Лагранжа Интегральное исчисление. Неопределенный интеграл. Определения. Свойства неопределенного интеграла. Таблица неопределенных интегралов. Интегрирование «по частям» для неопределенного интеграла. Метод подстановки (замены) в неопределенном интеграле. Интегрирование дробно-рациональных функций. Интегрирование простейших дробей. Интегрирование тригонометрических выражений. Универсальные тригонометрич. подстановки. Интегрирование иррациональных выражений. Теорема Чебышева. Определенный интеграл. Определение. Основные свойства. Формула Ньютона –Лейбница. Замена переменной и интегрирование «по частям» в определенном интеграле. Несобственные интегралы I и II рода. Определение. Метод исследования на сходимость. Приложения определенного интеграла. Вычисление площади. Приложение определенного интеграла. Вычисление длины дуги, Объема тела Дифференциальные уравнения. Основные понятия. Определения. Дифференциальные уравнения первого порядка., допускающее аналитическое решение. Уравнения с разделяющимися переменными. Однородное и приводящееся к однородному дифференциальное уравнение. Линейные Дифференциальные уравнения первого порядка. Метод вариации. Уравнения Бернулли и Дифференциальные уравнения в полных дифференциалах Дифференциальные уравнения высшего порядка, допускающие понижение степени. Линейные Дифференциальные уравнения высшего порядка. Свойства решений. Линейные Дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера. Подбор частного решения линейных Дифференциальных уравнений по виду правой части специального вида.
Метод вариации при решении ЛНДУ с произвольной правой частью. 34 Системы Дифференциальных уравнений; понятия, определения, метод исключения неизвестного Операционное исчисление. Определение. Таблицы и свойства оригинала и изображения. Операционный метод решения ЛНДУ высшего порядка. Операционный метод решения систем линейных уравнений. Основные формулы Определение производной
Уравнение касательной
Правила дифференцирования
Таблица основных производных
Логарифмическое дифференцирование
Правило Лопиталя
Формула Тейлора
Частные производные
Вопросы и ответы 1 ФНП. Основные понятия,определения. Непрерывность Ф.Н.П.
определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.
Определение Функция
Где Таким образом, Дифференциал функции нескольких переменных, как и в случае одной переменной, Представляет главную, линейную часть относительно приращений Теорема Если частные производные функции | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Частные производные | 
| 
| 
|
Рассмотрим изменение функции
 При задании приращения только одному из ее аргументов – ХI, и назовем его
При задании приращения только одному из ее аргументов – ХI, и назовем его 
Обозначения:
Замечание. При практическом вычислении частных производных пользуемся обычными правилами дифференцирования функции одной переменной, полагая аргумент, по которому ведется дифференцирование, переменным, а остальные аргументы – постоянными. Примеры.
|
| Дифференциал. Производные сложных функций | 
| 
| 
|
Дифференцируемость ФНП
Пусть функция z(f,y) дифференцируема по x и y.
Приращение функции 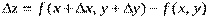 называют полным приращением.
называют полным приращением.
Полное приращение функции весьма сложно выражается через приращения независимых переменных D x, D y. Можно показать, что
 , где
, где  .
.
Сумма 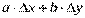 называется полным дифференциалом функции z=f(x,y).
называется полным дифференциалом функции z=f(x,y).
Определение: полным дифференциалом функции двух независимых
переменных называется главная часть полного приращения
функции, линейная относительно приращений независимых
переменных.
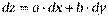 , D x=dx, D y=dy (1)
, D x=dx, D y=dy (1)
Теорема: полный дифференциал функции двух независимых переменных равен
сумме произведений частных производных функции на дифференциалы
соответствующих независимых переменных.
|
|
Доказательство:
Формула (1) справедлива при произвольных dx и dy. В частности, при dy =0:

Аналогично доказывается, что 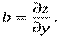
Тогда 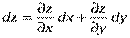 или
или 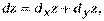
то есть дифференциал функции двух независимых переменных равен сумме ее частных дифференциалов.
Определение: функция двух независимых переменных, имеющая в некоторой
точке дифференциал, называется дифференцируемой в этой точке.
Теорема: если функция z=f(x,y) имеет в точке P(x,y) непрерывные частные
производные 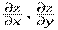 , то в этой точке функция дифференцируема.
, то в этой точке функция дифференцируема.
Определение
Градиентом функции  в точке М называется Вектор, координаты которого равны соответственно частным производным
в точке М называется Вектор, координаты которого равны соответственно частным производным  в этой точке.
в этой точке.
Для обозначения градиента функции используется обозначение grad u:
Grad u =  . .
| (6.5.2) |
Поскольку единичный вектор  имеет координаты
имеет координаты  , то производная по направлению для случая функции трех переменных запишется в виде
, то производная по направлению для случая функции трех переменных запишется в виде
 Grad U, Grad U,
| (6.5.3) |
Т. е. имеет форму Скалярного произведения векторов  и grad U.
и grad U.
Таким образом, Градиент функции характеризует Направление и Величину максимальной скорости возрастания этой функции в точке.
Предел отношения
 Называется Производной от функции U = F (X, Y, Z) По направлению вектора S и обозначается
Называется Производной от функции U = F (X, Y, Z) По направлению вектора S и обозначается 
|
При этом
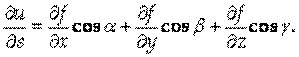
|
| Вектор, координатами которого в каждой точке некоторой области являются частные производные функции U = F (X, Y, Z) в этой точке, называется Градиентомфункции U = F (X, Y, Z). |
Обозначение:

Свойства градиента
1. Производная  по направлению некоторого вектора S Равняется проекции вектора grad U на вектор S.
по направлению некоторого вектора S Равняется проекции вектора grad U на вектор S.
Доказательство.
Единичный вектор направления S имеет вид ES ={cosα, cosβ, cosγ}, поэтому правая часть формулы (4.7) представляет собой скалярное произведение векторов grad U и Es, то есть указанную проекцию.
2. Производная в данной точке по направлению вектора S имеет наибольшее значение, равное |grad U |, если это направление совпадает с направлением градиента.
Доказательство.
Обозначим угол между векторами S И grad U Через J. Тогда из свойства 1 следует, что

Следовательно, ее наибольшее значение достигается при J =0 и равно |grad U |.
3. Производная по направлению вектора, перпендикулярного к вектору grad U, равна нулю.
Доказательство.
В этом случае
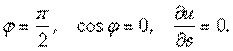
4. Если Z = F (X,Y) – функция двух переменных, то

Направлен перпендикулярно к линии уровня F (X,Y) = C, проходящей через данную точку
 Плоскость, определяемая этим уравнением, называется Касательной плоскостьюк графику функции Z= F (X, Y) в точке с координатами (х0,у0,Z0).
Плоскость, определяемая этим уравнением, называется Касательной плоскостьюк графику функции Z= F (X, Y) в точке с координатами (х0,у0,Z0).
|
|
|
Доказательство.
Рассмотрим выражение

И введем вспомогательную функцию

Тогда

Из условия теоремы следует, что J (Х) дифференцируема на отрезке [ X, X+ Δ X ], поэтому к ней можно применить теорему Лагранжа:

Так как в окрестности точки М определена  дифференцируема на отрезке [ Y, Y + Δ Y ], поэтому к полученной разности вновь можно применить теорему Лагранжа:
дифференцируема на отрезке [ Y, Y + Δ Y ], поэтому к полученной разности вновь можно применить теорему Лагранжа:
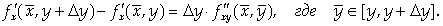
Тогда

Изменим порядок слагаемых в выражении для А:

И введем другую вспомогательную функцию

Проведя те же преобразования, что и для  , получим, что
, получим, что


Следовательно,

В силу непрерывности  и
и 
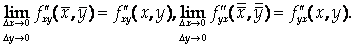 .
.
Поэтому, переходя к пределу при  получаем, что
получаем, что

Что и требовалось доказать.
Следствие. Указанное свойство справедливо для производных любого порядка и для функций от любого числа переменных.
Теорема 2
Смешанные производные второго порядка равны, если они непрерывны: 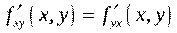
Следствие
Смешанные производные высших порядков равны, если непрерывны и получены по одним и тем же переменным одинаковое число раз, но может быть в разной последовательности.
Формула Тейлора для ФНП
Пусть имеется функция независимых переменных и, имеющая непрерывные частные производные всех порядков до  -го включительно в некоторой окрестности точки
-го включительно в некоторой окрестности точки  . Пусть точка
. Пусть точка 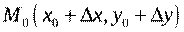 принадлежит этой окрестности. Определим на отрезке
принадлежит этой окрестности. Определим на отрезке 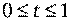 вспомогательную функцию
вспомогательную функцию  :
:
 , (3)
, (3)
где  . Согласно формуле Тейлора, имеем:
. Согласно формуле Тейлора, имеем:
 (4)
(4)
Вычислим коэффициенты формула (4) с помощью равенства (3). При  имеем
имеем  . Дифференцируя сложную функцию по
. Дифференцируя сложную функцию по  получим:
получим:
 ,
,
Заменив в последнем равенстве на  , а в остальных положим, найдем:
, а в остальных положим, найдем:

Если подставим найденные выражения в равенство (4) и затем положим  , то получим формулу Тейлора:
, то получим формулу Тейлора:

Формула Тейлора для функции нескольких переменных.
Напомним, что в случае функции одного переменного  формула Тейлора имеет вид
формула Тейлора имеет вид


где x₀- фиксированная точка, в которой ведётся разложение, x- текущая точка, а xt- некоторая точка отрезка между точками x₀ и x. При этом предполагается, что функция f имеет производную (m+ 1)-го порядка, определённую в некоторой окрестности точки x₀.
Последнее слагаемое формулы, то есть  называется остаточным членом формулы Тейлора, а многочлен от x, равный
называется остаточным членом формулы Тейлора, а многочлен от x, равный

называется многочленом Тейлора функции f в точке x₀.
,
Доказательство.
Напишем формулу Тейлора второго порядка для функции F (X, Y), помня о том, что в стационарной точке частные производные первого порядка равны нулю:

Если угол между отрезком М0М, где М (х0+ D Х, у0+ D У), и осью О Х обозначить J, то D Х = D R cos J, D Y = D R Sin J. При этом формула Тейлора примет вид:

Пусть  Тогда можно разделить и умножить выражение в скобках на А. Получим:
Тогда можно разделить и умножить выражение в скобках на А. Получим:


| 
| 
|
Интегральное исчисление. Неопределенный интеграл. Определения.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Первообразная функция. Понятие неопределенного интеграла.
Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции. Интегральное исчисление решает обратную задачу — нахождение самой функции по ее производной или дифференциалу.
|
|
Функция  называется первообразной функцией для функции
называется первообразной функцией для функции  на промежутке
на промежутке  , если в каждой точке
, если в каждой точке  этого промежутка
этого промежутка  .
.
Например,  является первообразной для функции
является первообразной для функции  , так как
, так как  .
.
Следует отметить, что для заданной функции  ее первообразная определена неоднозначно. Дифференцируя, нетрудно убедиться, что все функции
ее первообразная определена неоднозначно. Дифференцируя, нетрудно убедиться, что все функции  , где
, где  — некоторое число, являются первообразными для функции
— некоторое число, являются первообразными для функции  .
.
Аналогично в общем случае, если  — некоторая первообразная для
— некоторая первообразная для  , то, поскольку
, то, поскольку  , функции вида
, функции вида  , где
, где  - произвольное число, также являются первообразными для
- произвольное число, также являются первообразными для  .
.
Совокупность всех первообразных для функции  на промежутке
на промежутке  называется неопределенным интегралом от функции
называется неопределенным интегралом от функции  и обозначается
и обозначается  , где
, где  — знак интеграла,
— знак интеграла,  — подынтегральная функция,
— подынтегральная функция,  — подынтегральное выражение. Таким образом,
— подынтегральное выражение. Таким образом,

где  — некоторая первообразная для
— некоторая первообразная для  ,
,  — произвольная постоянная.
— произвольная постоянная.
Например,  - первообразная для функции
- первообразная для функции  , то
, то  .
.
Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции.
,
11 Свойства неопределенного интеграла. Таблица неопределенных интегралов.
Пример

Больше примеров решений→
2. Производная от неопределенного интеграла равна подынтегральной функции

Пример

Больше примеров решений→
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная

Пример

Больше примеров решений→
4. Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла

Пример

Больше примеров решений→
5. Неопределенный интеграл от суммы/разности двух и больше функций равен сумме/разности неопределенных интегралов от этих функций

Пример
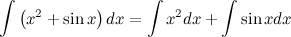
Больше примеров решений→
6. Если  , то и
, то и 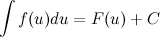 , где функция
, где функция 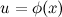 - произвольная функция с непрерывной производной.
- произвольная функция с непрерывной производной.
Пример
Известно, что  , а тогда
, а тогда

12 Интегрирование «по частям» для неопределенного интеграла.
Интегрирование по частям.
Пусть  и
и  — дифференцируемые функции. По свойству дифференциала
— дифференцируемые функции. По свойству дифференциала

или
 .
.
Интегрируя левую и правую части последнего равенства, получаем формулу интегрирования по частям для неопределенного интеграла
 .
.
Пример. Найти  .
.
Решение. 
 .
.
Пример. Найти  .
.
Решение.

 .
.
Пример. Найти  .
.
Положим  Тогда
Тогда  и
и  Применяя формулу интегрирования по частям, получаем
Применяя формулу интегрирования по частям, получаем

Повторное применение формулы интегрирования по частям приводит к табличному интегралу. Действительно, положим теперь 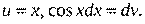 Тогда
Тогда  Следовательно,
Следовательно,

Пример


Формула Ньютона-Лейбница
Интеграл вида  называют интегралом с переменным верхним пределом.
называют интегралом с переменным верхним пределом.
Теорема. Пусть функция непрерывна на отрезке. Тогда  есть первообразная функции:
есть первообразная функции:

для любого  .
.
Доказательство. Пусть 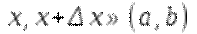 . Тогда по теореме о среднем
. Тогда по теореме о среднем

для некоторой точки  Следовательно,
Следовательно,  при, ибо в этом случае
при, ибо в этом случае  , а функция непрерывна.□
, а функция непрерывна.□
Формула Ньютона-Лейбница. Пусть  -- первообразная функции. Тогда
-- первообразная функции. Тогда

Доказательство. Для функции имеем в распоряжении две первообразных и. По теореме о первообразных найдется константа такая, что

Подставим в соотношение (3) вместо  сначала и получим
сначала и получим  , а затем подставим
, а затем подставим  в (3) – получим
в (3) – получим

что и требовалось доказать.
Несобственные интегралы
Пусть функция задана на полуинтервале  , где
, где  , а величина
, а величина  может быть как конечным числом, так и
может быть как конечным числом, так и  . Предположим, что интегрируема на любом отрезке,
. Предположим, что интегрируема на любом отрезке, 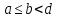 . Полагаем по определению
. Полагаем по определению

и называем это число несобственным интегралом. В случае, когда предел (1) существует, то говорим, что соответствующий интеграл сходится; в противном случае будем говорить, что он расходится.
Пусть функция  определена для всех
определена для всех  , где
, где  - некоторое число, и интегрируема на любом отрезке
- некоторое число, и интегрируема на любом отрезке  , где
, где  . Если существует конечный предел
. Если существует конечный предел
 ,
,
то говорят, что функция  интегрируема в несобственном смысле на промежутке
интегрируема в несобственном смысле на промежутке  . Этот предел называется несобственным интегралом с бесконечным пределом или несобственным интегралом первого рода и обозначается
. Этот предел называется несобственным интегралом с бесконечным пределом или несобственным интегралом первого рода и обозначается

Обычно, если конечный предел существует, то говорят, что несобственный интеграл сходится. Если же конечного предела не существует, то говорят, что несобственный интеграл расходится.
Приложение определенного интеграла. Вычисление длины дуги, Объема тела

| 
| 
| |
| Объём тела | 
| 
| 
|
Если площадь  сечения тела плоскостью, перпендикулярной оси сечения тела плоскостью, перпендикулярной оси  , является непрерывной функцией на отрезке , является непрерывной функцией на отрезке  , то объём тела вычисляется по формуле: , то объём тела вычисляется по формуле:
 . (25)
Объем тела, образованного вращением вокруг оси . (25)
Объем тела, образованного вращением вокруг оси  фигуры, ограниченной кривыми фигуры, ограниченной кривыми 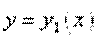 , , 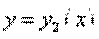 ( ( ) и прямыми ) и прямыми  , вычисляется по формуле: , вычисляется по формуле:
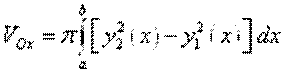 . (26)
Задание 1. Вычислить площадь фигуры, ограниченной линиями . (26)
Задание 1. Вычислить площадь фигуры, ограниченной линиями  и и  . Сделать чертеж.
Решение. Найдем точки пересечения кривых: . Сделать чертеж.
Решение. Найдем точки пересечения кривых:
 ,
Откуда ,
Откуда  . Тогда по формуле вычисления площади плоской фигуры (16) имеем: . Тогда по формуле вычисления площади плоской фигуры (16) имеем:  Сделаем чертеж.
Сделаем чертеж.

|
Дифференциальные уравнения. Основные понятия. Определения.
| Основные понятия | 
| 
| |
|
| Поделиться: |









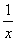























 из множества
из множества  по какому–либо закону ставится в соответствие некоторое Число
по какому–либо закону ставится в соответствие некоторое Число  из некоторого числового множества
из некоторого числового множества  . Тогда будем говорить, что на множестве
. Тогда будем говорить, что на множестве 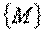 Задана функция
Задана функция  . При этом множества
. При этом множества  и
и  называются соответственно Областью определения и Областью значений функции
называются соответственно Областью определения и Областью значений функции  .
.
1. Функция
.
.
1. Функция  , где
, где  – постоянные числа, называется Линейной. Ее можно рассматривать как сумму N линейных функций от переменных
– постоянные числа, называется Линейной. Ее можно рассматривать как сумму N линейных функций от переменных  .
2. Функция
.
2. Функция  (
(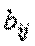 – постоянные числа) называется Квадратической. В отличие от предыдущего примера квадратическая функция не является сепарабельной, т. е. не раскладывается в сумму функций одной переменной.
Пример
Рассмотрим функцию
– постоянные числа) называется Квадратической. В отличие от предыдущего примера квадратическая функция не является сепарабельной, т. е. не раскладывается в сумму функций одной переменной.
Пример
Рассмотрим функцию  . Областью определения этой функции является вся координатная плоскость Oxy. Областью значений – промежуток
. Областью определения этой функции является вся координатная плоскость Oxy. Областью значений – промежуток  . Данная функция представляет собой Параболоид..
Определение
Линией уровня функции двух переменных
. Данная функция представляет собой Параболоид..
Определение
Линией уровня функции двух переменных  называется множество точек на плоскости, таких, что во всех этих точках значение функции одно и то же и равно C.
Пусть функция
называется множество точек на плоскости, таких, что во всех этих точках значение функции одно и то же и равно C.
Пусть функция  . Возьмем точку
. Возьмем точку  , любая e–окрестность которой содержит точки множества
, любая e–окрестность которой содержит точки множества  .
Определение
Функция
.
Определение
Функция  называется Непрерывной в точке А, если предел функции в этой точке Существует и Равен значению функции в этой точке:
называется Непрерывной в точке А, если предел функции в этой точке Существует и Равен значению функции в этой точке:
 .
Определение
Функция
.
Определение
Функция 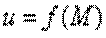 называется Непрерывной на множестве
называется Непрерывной на множестве  , если она непрерывна в любой точке этого множества.
Точки, в которых функция не обладает свойством непрерывности, называются Точками разрыва.
, если она непрерывна в любой точке этого множества.
Точки, в которых функция не обладает свойством непрерывности, называются Точками разрыва.
 называется Дифференцируемой в точке
называется Дифференцируемой в точке 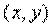 , если ее полное приращение может быть представлено в виде
, если ее полное приращение может быть представлено в виде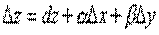
 – дифференциал функции,
– дифференциал функции, 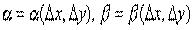 – бесконечно малые при
– бесконечно малые при  .
. , часть полного приращения функции.
, часть полного приращения функции.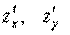 существуют в окрестности точки
существуют в окрестности точки 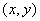 и непрерывны в самой точке
и непрерывны в самой точке  Дифференцируема В этой точке.
Дифференцируема В этой точке.