
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные Дифференциальные уравнения высшего порядка. Свойства решений.Содержание книги
Поиск на нашем сайте
Рассмотрим уравнение вида Определение. Выражение Линейный дифференциальный оператор обладает следующими свойствами: 1) 2) Решения линейного однородного уравнения обладают следующими свойствами: 1) Если функция у1 является решением уравнения, то функция С у1, где С – постоянное число, также является его решением. 2) Если функции у1 и у2 являются решениями уравнения, то у1 +у2 также является его решением. Линейные Дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера.
Теорема (Коши) Пусть для системы дифференциальных уравнений первого порядка (8.7.2) выполняются следующие условия: - функции - частные производные Тогда Существует одна и только Одна система решений уравнений (2):
Определенная в некоторой окрестности точки
Условия (8.7.5) называются Начальными условиями решения, а задача отыскания решения по заданным начальным условиям – Задачей Коши. Совокупность n функций
Зависящих от x и n произвольных постоянных Совокупность n функций
Получающееся из общего решения (6) системы (8.7.2) при определенных значениях постоянных Если в области
Относительно Одним из основных методов нахождения решения нормальных систем является метод исключения постоянных. С помощью этого метода данная система сводится к одному уравнению n–го порядка относительно одной неизвестной функции. |
Дифференциальное уравнение вида
 (1)
(1)
где 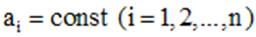 , f - известная функция, называется линейным дифференциальным уравнением n - го порядка с постоянными коэффициентами. Если
, f - известная функция, называется линейным дифференциальным уравнением n - го порядка с постоянными коэффициентами. Если 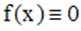 , то уравнение (1) называется однородным, в противном случае - неоднородным. К однородному уравнению, очевидно, применима теорема существования и единственности, причем интервалом определения решений этого уравнения будет вся действительная ось.
, то уравнение (1) называется однородным, в противном случае - неоднородным. К однородному уравнению, очевидно, применима теорема существования и единственности, причем интервалом определения решений этого уравнения будет вся действительная ось.
Если f - непрерывная функция, то общее решение уравнения (1) состоит из суммы общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения (1).
Чтобы решить однородное линейное уравнение с постоянными коэффициентами (1) надо составить характеристическое уравнение
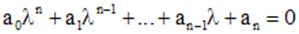 (2)
(2)
и найти его корни 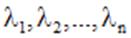 . Каждому простому корню
. Каждому простому корню 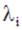 соответствует частое решение однородного уравнения (1), имеющее вид
соответствует частое решение однородного уравнения (1), имеющее вид 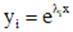 , а каждому корню
, а каждому корню  кратности k - решения
кратности k - решения  . Произвольная линейная комбинация всех частных решений является общим решением однородного уравнения (1), т.е.
. Произвольная линейная комбинация всех частных решений является общим решением однородного уравнения (1), т.е.
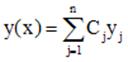 ,
,
где  произвольные постоянные.
произвольные постоянные.
Если все коэффициенты однородного уравнения (1) вещественные, то решение можно написать в вещественной форме и в случае комплексных корней  . Для каждой пары комплексно сопряженных корней
. Для каждой пары комплексно сопряженных корней  в формулу общего решения включаются слагаемые
в формулу общего решения включаются слагаемые
 ,
,
если эти корни простые, и слагаемые
 ,
,
если каждый из корней  имеет кратность k. Здесь
имеет кратность k. Здесь 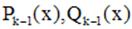 - многочлены степени k-1.
- многочлены степени k-1.
Метод Эйлера
Рассмотрим дифференциальное уравнение
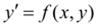 (1)
(1)
с начальным условием
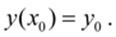
Подставив  в уравнение (1), получим значение производной в точке
в уравнение (1), получим значение производной в точке 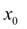 :
:
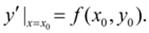
При малом 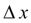 имеет место:
имеет место:
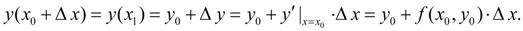
Обозначив  , перепишем последнее равенство в виде:
, перепишем последнее равенство в виде:
 (2)
(2)
Принимая теперь 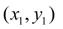 за новую исходную точку, точно также получим:
за новую исходную точку, точно также получим:
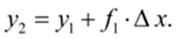
В общем случае будем иметь:
 (3)
(3)
Это и есть метод Эйлера. Величина 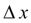 называется шагом интегрирования. Пользуясь этим методом, мы получаем приближенные значения у, так как производная
называется шагом интегрирования. Пользуясь этим методом, мы получаем приближенные значения у, так как производная 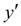 на самом деле не остается постоянной на промежутке длиной
на самом деле не остается постоянной на промежутке длиной 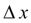 . Поэтому мы получаем ошибку в определении значения функции у, тем большую, чем больше
. Поэтому мы получаем ошибку в определении значения функции у, тем большую, чем больше 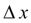 . Метод Эйлера является простейшим методом численного интегрирования дифференциальных уравнений и систем. Его недостатки – малая точность и систематическое накопление ошибок.
. Метод Эйлера является простейшим методом численного интегрирования дифференциальных уравнений и систем. Его недостатки – малая точность и систематическое накопление ошибок.
|
| Поделиться: |

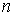 -го порядка называется Линейным, если неизвестная функция и все ее производные входят в уравнение линейно, то есть если уравнение имеет вид
-го порядка называется Линейным, если неизвестная функция и все ее производные входят в уравнение линейно, то есть если уравнение имеет вид
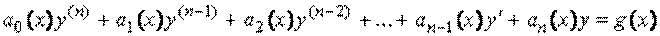 , (3.1)
Где
, (3.1)
Где 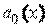 ,
, 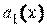 ,
, 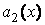 , …,
, …, 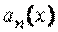 – некоторые функции независимой переменной, называемые коэффициентами дифференциального уравнения, а функция
– некоторые функции независимой переменной, называемые коэффициентами дифференциального уравнения, а функция 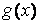 называется правой частью. Пусть все функции
называется правой частью. Пусть все функции 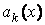 ,
, 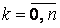 ,
,  и
и 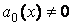 .
Разделим уравнение (3.1) почленно на коэффициент
.
Разделим уравнение (3.1) почленно на коэффициент 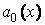 при старшей производной и обозначим
при старшей производной и обозначим
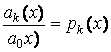 ,
, 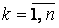 ,
, 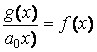 .
Тогда уравнение (3.1) примет вид
.
Тогда уравнение (3.1) примет вид
 . (3.2)
При этом все функции
. (3.2)
При этом все функции 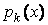 ,
,  непрерывны в
непрерывны в 
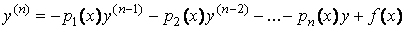 .
Продифференцируем правую часть этого равенства по
.
Продифференцируем правую часть этого равенства по 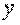 ,
,  ,
, 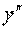 , …,
, …, 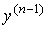 . Производные будут соответственно равны:
. Производные будут соответственно равны:
 ,
, 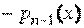 , …,
, …,  .
Поскольку эти функции непрерывны в
.
Поскольку эти функции непрерывны в 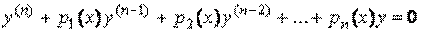 . (3.3)
Если же в уравнении (3.2)
. (3.3)
Если же в уравнении (3.2)  , то линейное уравнение называется Неоднородным. Вначале будут рассматриваться только однородные линейные уравнения, то есть уравнения вида (3.3).
, то линейное уравнение называется Неоднородным. Вначале будут рассматриваться только однородные линейные уравнения, то есть уравнения вида (3.3).
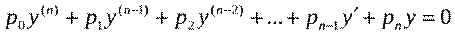
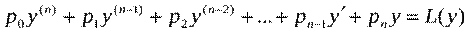 называется линейным дифференциальным оператором.
называется линейным дифференциальным оператором.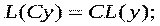


 – искомые функции,
– искомые функции,  – их производные, называется Системой дифференциальных уравнений первого порядка.
– их производные, называется Системой дифференциальных уравнений первого порядка. .
.
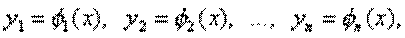
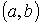 , называется Решением нормальной системы (8.7.2), если эти функции при подстановке в уравнение системы (8.7.2) обращают их в тождество.
, называется Решением нормальной системы (8.7.2), если эти функции при подстановке в уравнение системы (8.7.2) обращают их в тождество.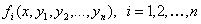 определены и непрерывны по всем аргументам в замкнутой области
определены и непрерывны по всем аргументам в замкнутой области  ,
, непрерывны в области
непрерывны в области 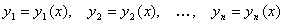 ,
,
 и Удовлетворяющая в этой точке заданным Начальным условиям:
и Удовлетворяющая в этой точке заданным Начальным условиям: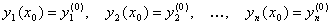 .
.
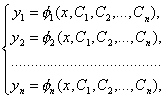
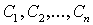 , будем называть Общим решением Системы (8.7.2) в некоторой области
, будем называть Общим решением Системы (8.7.2) в некоторой области 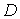 , если при любых значениях постоянных
, если при любых значениях постоянных 
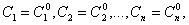 будем называть частным решением системы (8.7.2).
будем называть частным решением системы (8.7.2).
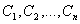 и подставить найденные значения постоянных в соотношения (8.7.6).
и подставить найденные значения постоянных в соотношения (8.7.6).


