
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операционный метод решения систем линейных уравнений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
, Системы линейных дифференциальных уравнений с постоянными коэффициентами можно решать операционными методами совершенно так же, как и отдельные уравнения; все отличие заключается лишь в том, что вместо одного изображающего уравнения приходим к системе таких уравнений, причем система эта в отношении изображений искомых функций будет линейно алгебраической. При этом никаких предварительных преобразований исходной системы дифференциальных уравнений производить не требуется ,) Таким образом. операционный метод позволяет в ряде случаев значительно упростить процедуру нахождения решения линейных дифференциальных уравнений и их систем. Основными первоначальными понятиями операционного исчисления являются понятия функции – оригинала и функции-изображения. Пусть f(t) – действительная функция действительного переменного t (под t понимается время или координата). Определение. Функция f(t) называется оригинало м, если она удовлетворяет следующим условиям: 1) f (t) = 0 при t < 0; 2) f (t) – кусочно-непрерывная при t 3) существуют такие числа M > 0 и S0 Число S0 называется показателем роста f(t). Условия (1-3) выполняются для большинства функций, описывающих различные физические процессы. Первое условие означает, что процесс начинается с некоторого времени; удобнее считать, что в момент t=0. Третьему условию удовлетворяют ограниченные функции (для них S0=0), степенные Определение. Изображением оригинала f(t) называется функция F(p) комплексного переменного р=
Операцию перехода от оригинала f(t) к изображению F(p) называют преобразованием Лапласа. Соответствие между оригиналом f(t) и изображением F(p) записывается в виде f(t) ÷ F(p). Принято оригиналы обозначать малыми буквами, а их изображения – соответствующими большими. Операционное исчисление строится на основе преобразования Лапласа. Преобразованием Лапласа или изображением по Лапласу функции
Интегралом Лапласа называется интеграл в правой части (1). Оригиналом называется функция вещественной переменной, которая удовлетворяет условиям: 1) 2) кусочно-непрерывна при 3) Функция может иметь на каждом отрезке при Иногда преобразованием Лапласа называется операция перехода от оригинала к изображению. Соответствие между и записывается в виде Пример: решить систему дифференциальных уравнений
, Основными понятиями операционного исчисления являются понятия оригинала и изображения. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ — метод математического анализа, позволяющий в ряде случаев посредством простых правил решать сложные математические задачи. . В основе этого метода лежит идея замены изучаемых функций (оригиналов) другими функциями (изображениями), получаемыми из первых по определенным правилам (обычно, изображение — функция, получаемая из данной преобразованием Лапласа), причем действия над оригиналами заменяются более простыми действиями над образами. Так, решение линейного дифференциального уравнения сводится к более простой задаче решения алгебраического уравнения; из алгебраического уравнения находят изображение решения данного уравнения, после чего по изображению восстанавливают само решение. Операции нахождения изображения по оригиналу (и наоборот) облегчаются наличием обширных таблиц «оригинал — изображение». Для развития операционного исчисления большое значение имели работы О. Хевисайда. Пользуясь этим методом, Хевисайд решил ряд задач электродинамики. Однако операционное исчисление не получило в трудах Хевисайда математического обоснования, многие его результаты оставались недоказанными. Строгое обоснование было дано с помощью интегрального преобразования Лапласа.
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 814; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.136.88 (0.01 с.) |

 0;
0; , т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции.
, т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции. (n > 0) и другие. Для функций вида
(n > 0) и другие. Для функций вида  , условие 3 не выполняется; не является оригиналом и функция f(t)=
, условие 3 не выполняется; не является оригиналом и функция f(t)=  - для неене выполняется 2-е условие.
- для неене выполняется 2-е условие. , определяемая интегралом
, определяемая интегралом
 вещественной переменной
вещественной переменной  называется функция
называется функция  комплексной переменной
комплексной переменной  , определяемая несобственным интегралом
, определяемая несобственным интегралом . (1)
. (1) при
при  ,
, ; (2)
; (2) при любом, где
при любом, где  некоторые постоянные числа. Число
некоторые постоянные числа. Число  называется п оказателем роста функции или абсциссой сходимости интеграла Лапласа.
называется п оказателем роста функции или абсциссой сходимости интеграла Лапласа. лишь конечное число точек разрыва первого рода.
лишь конечное число точек разрыва первого рода. .
.

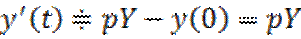

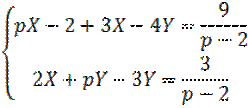
 ,
,
 ,
, .
.
 .
.


