
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование по частям в определённом интегралеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Интегрирование по частям. Пусть
Доказательство. Соотношение Пример 2. Вычислим
Заметим, что Вычисление определенного интеграла заменой переменных и по частям. Теорема. Пусть функция Тогда справедливо следующее равенство
Эта формула носит название формулы замены переменной в определенном интеграле. Теорема. Пусть функции
Эта формула называется формулой интегрирования по частям для определенного интеграла.
20 Несобственные интегралы I и II рода. Определение. Метод исследования на сходимость. Исследование на сходимость и вычисление Чтобы существовал определенный интеграл, то есть существовал предел интегральной суммы, должны выполняться два условия:
Сходящиеся несобственные интегралы обладают всеми свойствами определенных интегралов. Вопрос о сходимости несобственных интегралов можно решить двумя способами. 1. Непосредственное вычисление. Если несложно определить первообразную, то можно вычислить определенный интеграл, затем найти его предел при поставленных условиях и сделать заключение: · если при вычислении несобственного интеграла получено любое число, то он сходится (к этому числу); · если получена
2. Применение признака сравнения. Не приводя теоремы о признаке сравнения, ограничимся только выводом из нее – практическим способом исследования несобственных интегралов на сходимость. 1 - Сравнивают подынтегральную функцию с функцией, вполне определенной для несобственных интегралов первого и второго рода.
Сравнение происходит путем определения функции, эквивалентной подынтегральной при условиях (см. тему 4, вычисление пределов): · для НИ-1: · для НИ-2
Несобственные интегралы Пусть функция задана на полуинтервале
и называем это число несобственным интегралом. В случае, когда предел (1) существует, то говорим, что соответствующий интеграл сходится; в противном случае будем говорить, что он расходится. Пусть функция то говорят, что функция Обычно, если конечный предел существует, то говорят, что несобственный интеграл сходится. Если же конечного предела не существует, то говорят, что несобственный интеграл расходится.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 546; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.117.77 (0.006 с.) |

 и
и  -- дифференцируемые функции на отрезке. Тогда
-- дифференцируемые функции на отрезке. Тогда
 проинтегрируем от а до b получим
проинтегрируем от а до b получим  что эквивалентно (2).
что эквивалентно (2).
 при условии
при условии 
 имеет непрерывную производную на отрезке
имеет непрерывную производную на отрезке  ,
, 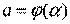 ,
,  и функция
и функция  непрерывна в каждой точке
непрерывна в каждой точке  вида
вида  , где
, где  .
.
 и
и  имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке  . Тогда
. Тогда где
где 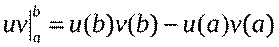 .
. на
на  не имеет разрывов второго рода.
не имеет разрывов второго рода.
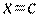 имеется разрыв второго рода, если хотя бы один из односторонних пределов функции в этой точке бесконечен или не существует:
имеется разрыв второго рода, если хотя бы один из односторонних пределов функции в этой точке бесконечен или не существует:  (см. тему 4, схема классификации разрывов).
Практически для определения точки разрыва надо найти точки, которые не входят в область допустимых значений, например, такие, в которых знаменатель обращается в ноль.
(см. тему 4, схема классификации разрывов).
Практически для определения точки разрыва надо найти точки, которые не входят в область допустимых значений, например, такие, в которых знаменатель обращается в ноль.
 на нем непрерывна.
на нем непрерывна.

 (А)
(А)
 (В)
(В)

 (А1)
(А1)
 (В1)
(В1)

 ).
).

 - (А1)
или
- (А1)
или  - (В1)
- (В1)
 . О несобственных интегралах от этих функций известно:
. О несобственных интегралах от этих функций известно:

 так же для
так же для 
 ;
;  ;
; (или
(или  ) - к точке разрыва функции,
) - к точке разрыва функции,  .
. , где
, где  , а величина
, а величина  может быть как конечным числом, так и
может быть как конечным числом, так и  . Предположим, что интегрируема на любом отрезке,
. Предположим, что интегрируема на любом отрезке, 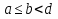 . Полагаем по определению
. Полагаем по определению
 определена для всех
определена для всех  , где
, где  - некоторое число, и интегрируема на любом отрезке
- некоторое число, и интегрируема на любом отрезке  , где
, где  . Если существует конечный предел
. Если существует конечный предел ,
, интегрируема в несобственном смысле на промежутке
интегрируема в несобственном смысле на промежутке  . Этот предел называется несобственным интегралом с бесконечным пределом или несобственным интегралом первого рода и обозначается
. Этот предел называется несобственным интегралом с бесконечным пределом или несобственным интегралом первого рода и обозначается



