Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование биноминальных дифференциалов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение: Биноминальным дифференциалом называется выражение X m (a + b x n)p dx где m, n, и p – рациональные числа. Как было доказано академиком Чебышевым П.Л. (1821-1894), интеграл от биноминального дифференциала может быть выражен через элементарные функции только в следующих трех случаях: 1. Если р – целое число, то интеграл рационализируется с помощью подстановки
2. Если
3) Если
18 Определенный интеграл. Определение. Основные свойства. Формула Ньютона –Лейбница.
Определение. Определённым интегралом функции на отрезке называется предел интегральных сумм, если параметр разбиения стремиться к нулю:
Это значит, что определенный интеграл есть такое число
Функция называется подинтегральной, Формула Ньютона-Лейбница Интеграл вида Теорема. Пусть функция непрерывна на отрезке. Тогда
для любого Доказательство. Пусть
для некоторой точки Формула Ньютона-Лейбница. Пусть
Доказательство. Для функции имеем в распоряжении две первообразных и. По теореме о первообразных найдется константа такая, что
Подставим в соотношение (3) вместо
что и требовалось доказать. Свойства определенного интеграла. 1. Постоянный множитель можно выносить за знак интеграла, т.е.
2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.
3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е.
4. Если на отрезке
т.е. обе части неравенства можно почленно интегрировать.
Основная теорема интегрального исчисления – формула Ньютона-Лейбница. Теорема. Пусть функция
Нахождение определенных интегралов с использованием формулы Ньютона—Лейбница осуществляется в два шага: на первом шаге, используя технику нахождения неопределенного интеграла, находят некоторую первообразную
19 Замена переменной и интегрирование «по частям» в определенном интеграле.
.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 539; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.92.213 (0.008 с.) |

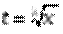 , где l - общий знаменатель m и n.
, где l - общий знаменатель m и n. - целое число, то интеграл рационализируется подстановкой
- целое число, то интеграл рационализируется подстановкой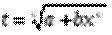 , где s – знаменатель числа р.
, где s – знаменатель числа р.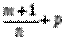 - целое число, то используется подстановка
- целое число, то используется подстановка 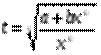 , где s – знаменатель числа р.
, где s – знаменатель числа р.


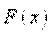 - первообразная непрерывной функции
- первообразная непрерывной функции  на отрезке
на отрезке 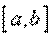 , то справедлива Формула Ньютона – Лейбница:
, то справедлива Формула Ньютона – Лейбница:
 . (7)
. (7)
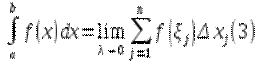
 , что для любого сколь угодно малого
, что для любого сколь угодно малого 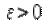 найдется такое
найдется такое 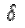 (зависящее от
(зависящее от 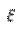 ), что для любого разбиения (1) с параметром
), что для любого разбиения (1) с параметром 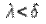 интегральная сумма
интегральная сумма 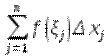 отличается от меньше чем на:
отличается от меньше чем на: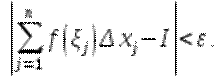
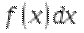 называется подинтегральным выражением. Число
называется подинтегральным выражением. Число 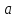 называется нижним пределом интегрирования, а
называется нижним пределом интегрирования, а 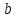 – верхним пределом интегрирования.
– верхним пределом интегрирования. называют интегралом с переменным верхним пределом.
называют интегралом с переменным верхним пределом. есть первообразная функции:
есть первообразная функции:
 .
.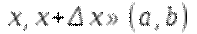 . Тогда по теореме о среднем
. Тогда по теореме о среднем
 Следовательно,
Следовательно,  при, ибо в этом случае
при, ибо в этом случае  , а функция непрерывна.□
, а функция непрерывна.□ -- первообразная функции. Тогда
-- первообразная функции. Тогда

 сначала и получим
сначала и получим  , а затем подставим
, а затем подставим  в (3) – получим
в (3) – получим
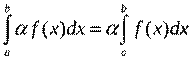
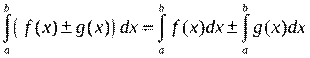
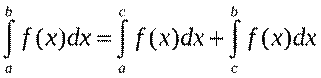
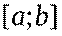
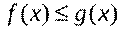 , то и
, то и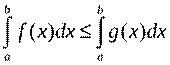 ,
,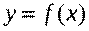 непрерывна на отрезке
непрерывна на отрезке 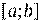 и
и 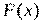 — любая первообразная для
— любая первообразная для  на
на 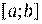 . Тогда определенный интеграл от функции
. Тогда определенный интеграл от функции 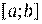 равен приращению первообразной
равен приращению первообразной 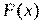 на этом отрезке, т.е.
на этом отрезке, т.е.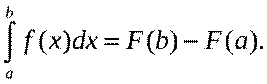
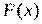 для подынтегральной функции
для подынтегральной функции 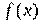 ; на втором применяется собственно формула Ньютона—Лейбница — находится приращение первообразной, равное искомому интегралу.
; на втором применяется собственно формула Ньютона—Лейбница — находится приращение первообразной, равное искомому интегралу.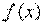 – непрерывная функция на отрезке
– непрерывная функция на отрезке 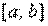 ;
2) функция
;
2) функция 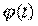 дифференцируема на
дифференцируема на 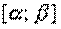 , а
, а 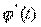 непрерывна на
непрерывна на 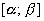 ;
3)
;
3) 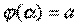 ,
, 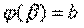 .
Тогда справедлива формула
.
Тогда справедлива формула