
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общий вид уравнения первого порядкаСодержание книги
Поиск на нашем сайте
Если уравнение (1) удается разрешить относительно
Задачей Коши называют задачу нахождения решения уравнения Дифференциальные уравнения первого порядка., допускающее аналитическое решение.
Существование и единственность решения дифференциального уравнения Определение Решением Дифференциального уравнения первого порядка называется функция В теории дифференциальных уравнений основной задачей является вопрос о существовании и единственности решения. Ответ на него дает Теорема Коши, которую мы приводим без доказательств. Теорема: (Теорема Коши). Пусть дано дифференциальное уравнение (8.2.2). Если функция Для любой внутренней точки Если два решения При соблюдении условий Теоремы Коши через каждую внутреннюю точку области
Задача нахождения решения уравнения (8.2.2), удовлетворяющих условию (8.2.3) называется Задачей Коши или иными словами – из множества интегральных кривых выделяется та, которая проходит через заданную точку В ряде случаев, когда условия теоремы Коши не выполнены, через некоторые точки плоскости Приведем Пример использования теоремы Коши. Пример: Решить уравнение
Решение В данном случае Функция Определение Общим решением уравнения (8.2.2) называется функция Определение Частным решением уравнения (8.2.2) в области |
| Линейные дифференциальные уравнения первого порядка |
Определение линейного уравнения первого порядка
Дифференциальное уравнение вида
 где a (x) и b (x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка. Мы рассмотрим два метода решения указанных уравнений:
· Использование интегрирующего множителя;
· Метод вариации постоянной.
Использование интегрирующего множителя
Если линейное дифференциальное уравнение записано в стандартной форме:
то интегрирующий множитель определяется формулой:
где a (x) и b (x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка. Мы рассмотрим два метода решения указанных уравнений:
· Использование интегрирующего множителя;
· Метод вариации постоянной.
Использование интегрирующего множителя
Если линейное дифференциальное уравнение записано в стандартной форме:
то интегрирующий множитель определяется формулой:
 Умножение левой части уравнения на интегрирующий множитель u (x) преобразует ее в производную произведения y (x) u (x). Общее решение диффференциального уравнения выражается в виде:
Умножение левой части уравнения на интегрирующий множитель u (x) преобразует ее в производную произведения y (x) u (x). Общее решение диффференциального уравнения выражается в виде:
 где C − произвольная постоянная.
Метод вариации постоянной
Данный метод аналогичен предыдущему подходу. Сначала необходимо найти общее решение однородного уравнения:
где C − произвольная постоянная.
Метод вариации постоянной
Данный метод аналогичен предыдущему подходу. Сначала необходимо найти общее решение однородного уравнения:
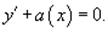 Общее решение однородного уравнения содержит постоянную интегрирования C. Далее мы заменяем константу C на некоторую (пока еще неизвестную) функцию C (x). Подставляя это решение в неоднородное дифференциальное уравнение, можно определить функцию C (x). Описанный алгоритм называется методом вариации постоянной. Разумеется, оба метода приводят к одинаковому результату.
Задача Коши
Если, кроме дифференциального уравнения, задано также начальное условие в форме y (x 0) = y 0, то такая задача называется задачей Коши. Решение задачи Коши не содержит произвольной константы C. Ее конкретное числовое значение определяется подстановкой общего решения уравнения в заданное начальное условие y (x 0) = y 0.
Общее решение однородного уравнения содержит постоянную интегрирования C. Далее мы заменяем константу C на некоторую (пока еще неизвестную) функцию C (x). Подставляя это решение в неоднородное дифференциальное уравнение, можно определить функцию C (x). Описанный алгоритм называется методом вариации постоянной. Разумеется, оба метода приводят к одинаковому результату.
Задача Коши
Если, кроме дифференциального уравнения, задано также начальное условие в форме y (x 0) = y 0, то такая задача называется задачей Коши. Решение задачи Коши не содержит произвольной константы C. Ее конкретное числовое значение определяется подстановкой общего решения уравнения в заданное начальное условие y (x 0) = y 0.
|
|
| Поделиться: |


 , то получится уравнение первого порядка, разрешенное относительно производной.
, то получится уравнение первого порядка, разрешенное относительно производной.
 , удовлетворяющего начальному условию
, удовлетворяющего начальному условию  (другая запись
(другая запись  ).
). ,
,
 – независимая переменная,
– независимая переменная,  и
и  – соответственно неизвестная функция и ее производная, называется Дифференциальным уравнением первого порядка.
– соответственно неизвестная функция и ее производная, называется Дифференциальным уравнением первого порядка. ,
,  ,
,  .
. , оно имеет вид
, оно имеет вид .
.
 ,
, 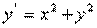 ,
,  .
. , откуда получаем два уравнения первого порядка:
, откуда получаем два уравнения первого порядка:  .
. , откуда
, откуда  .
. , откуда
, откуда  .
. , определенная на некотором интервале
, определенная на некотором интервале  , которая при подстановке уравнение (8.2.1) обращает его в тождество.
, которая при подстановке уравнение (8.2.1) обращает его в тождество. и ее частная производная
и ее частная производная  непрерывны в некоторой области
непрерывны в некоторой области  плоскости
плоскости  , тогда:
, тогда: Найдется решение уравнения (8.2.2), удовлетворяющее условию
Найдется решение уравнения (8.2.2), удовлетворяющее условию  при
при  .
. и
и  уравнения (8.2.2) совпадают хотя бы для одного значения
уравнения (8.2.2) совпадают хотя бы для одного значения  , т. е.
, т. е.  , то эти решения Совпадают для всех
, то эти решения Совпадают для всех 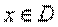 .
. в фиксированной точке
в фиксированной точке  , есть Начальные условия (или Условия Коши) и записываются в такой форме:
, есть Начальные условия (или Условия Коши) и записываются в такой форме: .
.
 области
области  либо не проходит ни одна интегральная кривая, либо проходит более одной интегральной кривой. Эти точки называются Особыми точками данного дифференциального уравнения.
либо не проходит ни одна интегральная кривая, либо проходит более одной интегральной кривой. Эти точки называются Особыми точками данного дифференциального уравнения. .
.
 ,
,  определены и дифференцируемы при любых
определены и дифференцируемы при любых  и
и  . Следовательно, условия теоремы выполнены на всей плоскости
. Следовательно, условия теоремы выполнены на всей плоскости  является Решением уравнения. Покажем, что это решение является общим решением уравнения (8.2.4). Пусть существует какое–либо другое решение уравнения (8.2.4)
является Решением уравнения. Покажем, что это решение является общим решением уравнения (8.2.4). Пусть существует какое–либо другое решение уравнения (8.2.4)  . Пусть
. Пусть  – точка, в которой это решение определено, и
– точка, в которой это решение определено, и  . Положим, что
. Положим, что 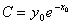 , тогда
, тогда 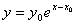 . В этом случае решения уравнения (8.2.4) совпадают в точке
. В этом случае решения уравнения (8.2.4) совпадают в точке  .
. , удовлетворяющая этому уравнению при произвольном значении постоянной
, удовлетворяющая этому уравнению при произвольном значении постоянной  , полученная при определенном значении постоянной
, полученная при определенном значении постоянной  .
.


