
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несобственный интеграл второго рода определяется по формулеСодержание книги
Поиск на нашем сайте
Если предел существует и конечен, то говорят, что несобственный интеграл сходится. Если же предел бесконечный либо вообще не существует, то говорят, что интеграл расходится.
К несобственным интегралам применимы методы замены переменной и интегрирования по частям.
Приложения определенного интеграла. Вычисление площади.
Вычисление площадей плоских фигур. Пусть функция Теорема. Пусть на отрезке
Приложение определенного интеграла. Вычисление длины дуги, Объема тела
Вычисление длины дуги плоской кривой 1 случай. Пусть в прямоугольных координатах на плоскости дана кривая (рис. 12).
Возьмем на дуге
Определение. Длиной
Длина всей дуги, заключенной между точками и, вычисляется по формуле
Дифференциальные уравнения. Основные понятия. Определения.
Определение Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции. Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется Обыкновенным, если от нескольких – то Уравнением в частных производных. Простейший Пример дифференциального уравнения дает задача о нахождении первообразной В общем случае Дифференциальное уравнение можно записать в виде
Где Основной задачей теории обыкновенных дифференциальных уравнений является нахождение функций, представляющих собой решения этих уравнений.
Определение Решением дифференциального уравнения (8.1.1) называется такая функция Например, функция Задача о нахождении решения некоторого дифференциального уравнения называется Задачей интегрирования данного дифференциального уравнения. График решения дифференциального уравнения называется Интегральной кривой. Пример Решить уравнение Решение Поскольку Отметим, что без дополнительных предположений решение данного уравнения принципиально неоднозначно. Другими словами, дифференциальное уравнение задает семейство интегральных кривых на плоскости. Для выделения однозначно определенной интегральной кривой (решения) в нашем случае достаточно указать точку плоскости, через которую проходит искомая интегральная кривая, и направление, в котором она проходит через эту точку. Дополнительные условия такого рода обычно называют Начальными условиями, поскольку часто дифференциальные уравнения используются для описания динамических процессов – процессов, происходящих во времени. Для выделения однозначно определенного решения дифференциального уравнения Определение Общим решением дифференциального уравнения (8.1.1)
Которое является функцией переменной Частным решением дифференциального уравнения называется решение, получаемое из общего решения при заданных конкретных значениях констант. В нашем Примере Чтобы построить дифференциальное уравнение, которому удовлетворяют кривые заданного семейства (8.1.2), нужно продифференцировать равенство Пример Составить дифференциальное уравнение семейства кривых Решение Дифференцируя заданную функцию, находим Основные понятия и определения дифференциальных уравнений Дифференциальным уравнением называется уравнение, связывающее независимую переменную
Если искомая функция Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Например, дифференциальное уравнение Решением дифференциального уравнения n-го порядка на интервале
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.100.107 (0.011 с.) |


 .
.


 И
И  , при условии, что функции
, при условии, что функции  - непрерывны и
- непрерывны и 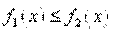 , и вертикальными прямыми
, и вертикальными прямыми  и
и  . Тогда площадь данной фигуры вычисляется по формуле:
. Тогда площадь данной фигуры вычисляется по формуле:
 . (16)
Если фигура ограничена кривой, которая задана параметрическими уравнениями
. (16)
Если фигура ограничена кривой, которая задана параметрическими уравнениями  ,
,  , прямыми
, прямыми  и осью
и осью  , то площадь данной фигуры вычисляется по формуле:
, то площадь данной фигуры вычисляется по формуле:
 , (17)
Где
, (17)
Где  .
Если фигура ограничена кривой, которая задана уравнением в полярных координатах
.
Если фигура ограничена кривой, которая задана уравнением в полярных координатах  , и двумя лучами
, и двумя лучами  , то площадь данной фигуры вычисляется по формуле:
, то площадь данной фигуры вычисляется по формуле:
 . (18)
. (18)
 неотрицательна и непрерывна на отрезке
неотрицательна и непрерывна на отрезке  . Тогда по геометрическому смыслу определенного интеграла площадь
. Тогда по геометрическому смыслу определенного интеграла площадь  под кривой
под кривой  на
на  , т.е.
, т.е.  .
. заданы непрерывные функции
заданы непрерывные функции  и
и  такие, что
такие, что 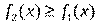 . Тогда площадь
. Тогда площадь 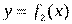 и
и  , на отрезке
, на отрезке 
 сечения тела плоскостью, перпендикулярной оси
сечения тела плоскостью, перпендикулярной оси  , является непрерывной функцией на отрезке
, является непрерывной функцией на отрезке  , то объём тела вычисляется по формуле:
, то объём тела вычисляется по формуле:
 . (25)
Объем тела, образованного вращением вокруг оси
. (25)
Объем тела, образованного вращением вокруг оси  фигуры, ограниченной кривыми
фигуры, ограниченной кривыми 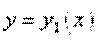 ,
, 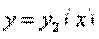 (
( ) и прямыми
) и прямыми  , вычисляется по формуле:
, вычисляется по формуле:
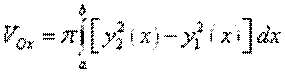 . (26)
Задание 1. Вычислить площадь фигуры, ограниченной линиями
. (26)
Задание 1. Вычислить площадь фигуры, ограниченной линиями  и
и  . Сделать чертеж.
Решение. Найдем точки пересечения кривых:
. Сделать чертеж.
Решение. Найдем точки пересечения кривых:
 ,
Откуда
,
Откуда  . Тогда по формуле вычисления площади плоской фигуры (16) имеем:
. Тогда по формуле вычисления площади плоской фигуры (16) имеем:  Сделаем чертеж.
Сделаем чертеж.

 . Вычислим длину дуги кривой, заключенной между точками
. Вычислим длину дуги кривой, заключенной между точками  и
и 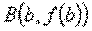

 точки
точки  с абсциссами
с абсциссами  и проведем хорды
и проведем хорды  , длины которых обозначим соответственно
, длины которых обозначим соответственно  . Тогда получим ломанную
. Тогда получим ломанную  , вписанную в дугу. Длина ломанной равна
, вписанную в дугу. Длина ломанной равна .
. дуги называется тот предел, к которому стремится длина вписанной ломанной, когда длина ее наибольшего звена стремится к нулю:
дуги называется тот предел, к которому стремится длина вписанной ломанной, когда длина ее наибольшего звена стремится к нулю: .
.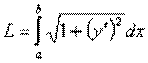 .
. , искомую функцию
, искомую функцию  и её производные
и её производные 
 (1)
Порядок наивысшей производной, входящей в данное уравнение, называется порядком дифференциального уравнения.
Функция
(1)
Порядок наивысшей производной, входящей в данное уравнение, называется порядком дифференциального уравнения.
Функция  называется Решением дифференциального уравнения (1) на промежутке
называется Решением дифференциального уравнения (1) на промежутке  , если уравнение (1) при подстановке в него функции
, если уравнение (1) при подстановке в него функции  вместе со своими производными обращается в тождество:
вместе со своими производными обращается в тождество:
 .
Общим решением дифференциального Уравнения (1) называется функция
.
Общим решением дифференциального Уравнения (1) называется функция  , (2)
Зависящая от переменой
, (2)
Зависящая от переменой  и
и 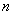 произвольных постоянных
произвольных постоянных  и удовлетворяющая следующим условиям:
1) при любых значениях произвольных постоянных
и удовлетворяющая следующим условиям:
1) при любых значениях произвольных постоянных  функция (2) является решением уравнения (1);
2) любое решение уравнения (1) может быть получено из функции (2) при соответствующих значениях постоянных
функция (2) является решением уравнения (1);
2) любое решение уравнения (1) может быть получено из функции (2) при соответствующих значениях постоянных  , определяющее общее решение уравнения (1) как неявную функцию, называется Общим интегралом Дифференциального уравнения (1).
Задача нахождения решения уравнения (1), удовлетворяющего начальным условиям:
, определяющее общее решение уравнения (1) как неявную функцию, называется Общим интегралом Дифференциального уравнения (1).
Задача нахождения решения уравнения (1), удовлетворяющего начальным условиям:
 ,
Где
,
Где  - заданные числа называется Задачей Коши
- заданные числа называется Задачей Коши
 для заданной функции
для заданной функции  , поскольку ее можно рассматривать как задачу о нахождении функции
, поскольку ее можно рассматривать как задачу о нахождении функции  , удовлетворяющей уравнению
, удовлетворяющей уравнению  .
. ,
,
 – некоторая функция от
– некоторая функция от  переменных, при этом порядок
переменных, при этом порядок  старшей производной, входящей в запись уравнения, называется Порядком дифференциального уравнения.
старшей производной, входящей в запись уравнения, называется Порядком дифференциального уравнения.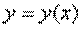 , которая при подстановке в это уравнение обращает его в тождество.
, которая при подстановке в это уравнение обращает его в тождество. является решением уравнения
является решением уравнения 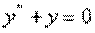 , так как
, так как 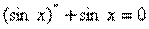 для всех
для всех  .
. .
. , то исходное уравнение равносильно следующему равенству дифференциалов
, то исходное уравнение равносильно следующему равенству дифференциалов  . Выполняя по членное интегрирование получаем
. Выполняя по членное интегрирование получаем  , где
, где  – произвольная постоянная. Вновь записывая производную как отношение двух дифференциалов, приходим к равенству
– произвольная постоянная. Вновь записывая производную как отношение двух дифференциалов, приходим к равенству  , интегрируя почленно окончательно получаем
, интегрируя почленно окончательно получаем  , где
, где  – произвольная постоянная.
– произвольная постоянная. –го порядка следует, вообще говоря, дополнительно задать
–го порядка следует, вообще говоря, дополнительно задать  ,
,
 и
и  – общее решение,
– общее решение,  – частное решение дифференциального уравнения
– частное решение дифференциального уравнения  .
.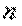 раз, а затем из полученных равенств исключить константы.
раз, а затем из полученных равенств исключить константы.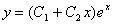 .
. ,
,  . Исключая из этих двух равенств
. Исключая из этих двух равенств 
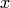 , искомую функцию
, искомую функцию 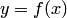 и её производные
и её производные  , т. е. уравнение вида
, т. е. уравнение вида
 есть функция одной независимой переменной, дифференциальное уравнение называется обыкновенным;
есть функция одной независимой переменной, дифференциальное уравнение называется обыкновенным; — уравнение первого порядка, дифференциальное уравнение
— уравнение первого порядка, дифференциальное уравнение  , где
, где  — известная функция, — уравнение второго порядка; дифференциальное уравнение
— известная функция, — уравнение второго порядка; дифференциальное уравнение  — уравнение 9-го порядка.
— уравнение 9-го порядка. называется функция
называется функция  , определенная на интервале вместе со своими производными до n-го порядка включительно, и такая, что подстановка функции в дифференциальное уравнение превращает последнее в тождество
, определенная на интервале вместе со своими производными до n-го порядка включительно, и такая, что подстановка функции в дифференциальное уравнение превращает последнее в тождество


