
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцирование сложной Ф.Н.П. неявной Ф.Н.П.Содержание книги
Поиск на нашем сайте
Градиент, производная по направлению ФНП, касательные плоскости Частные производные и дифференциалы высшего порядка Формула Тейлора для ФНП Экстремум ФНП. Необходимое условие экстремума ФНП Достаточное условие экстремума ФНП, критерий Сильвестра Условный экстремум ФНП. Метод множителей Лагранжа Интегральное исчисление. Неопределенный интеграл. Определения. Свойства неопределенного интеграла. Таблица неопределенных интегралов. Интегрирование «по частям» для неопределенного интеграла. Метод подстановки (замены) в неопределенном интеграле. Интегрирование дробно-рациональных функций. Интегрирование простейших дробей. Интегрирование тригонометрических выражений. Универсальные тригонометрич. подстановки. Интегрирование иррациональных выражений. Теорема Чебышева. Определенный интеграл. Определение. Основные свойства. Формула Ньютона –Лейбница. Замена переменной и интегрирование «по частям» в определенном интеграле. Несобственные интегралы I и II рода. Определение. Метод исследования на сходимость. Приложения определенного интеграла. Вычисление площади. Приложение определенного интеграла. Вычисление длины дуги, Объема тела Дифференциальные уравнения. Основные понятия. Определения. Дифференциальные уравнения первого порядка., допускающее аналитическое решение. Уравнения с разделяющимися переменными. Однородное и приводящееся к однородному дифференциальное уравнение. Линейные Дифференциальные уравнения первого порядка. Метод вариации. Уравнения Бернулли и Дифференциальные уравнения в полных дифференциалах Дифференциальные уравнения высшего порядка, допускающие понижение степени. Линейные Дифференциальные уравнения высшего порядка. Свойства решений. Линейные Дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера. Подбор частного решения линейных Дифференциальных уравнений по виду правой части специального вида. Метод вариации при решении ЛНДУ с произвольной правой частью. 34 Системы Дифференциальных уравнений; понятия, определения, метод исключения неизвестного Операционное исчисление. Определение. Таблицы и свойства оригинала и изображения. Операционный метод решения ЛНДУ высшего порядка. Операционный метод решения систем линейных уравнений. Основные формулы Определение производной
Уравнение касательной
Правила дифференцирования
Таблица основных производных
Логарифмическое дифференцирование
Правило Лопиталя
Формула Тейлора
Частные производные
Вопросы и ответы 1 ФНП. Основные понятия,определения. Непрерывность Ф.Н.П.
определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 722; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.008 с.) |









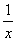


























 из множества
из множества  по какому–либо закону ставится в соответствие некоторое Число
по какому–либо закону ставится в соответствие некоторое Число  из некоторого числового множества
из некоторого числового множества  . Тогда будем говорить, что на множестве
. Тогда будем говорить, что на множестве 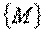 Задана функция
Задана функция  . При этом множества
. При этом множества  и
и  называются соответственно Областью определения и Областью значений функции
называются соответственно Областью определения и Областью значений функции  .
.
1. Функция
.
.
1. Функция  , где
, где  – постоянные числа, называется Линейной. Ее можно рассматривать как сумму N линейных функций от переменных
– постоянные числа, называется Линейной. Ее можно рассматривать как сумму N линейных функций от переменных  .
2. Функция
.
2. Функция  (
(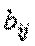 – постоянные числа) называется Квадратической. В отличие от предыдущего примера квадратическая функция не является сепарабельной, т. е. не раскладывается в сумму функций одной переменной.
Пример
Рассмотрим функцию
– постоянные числа) называется Квадратической. В отличие от предыдущего примера квадратическая функция не является сепарабельной, т. е. не раскладывается в сумму функций одной переменной.
Пример
Рассмотрим функцию  . Областью определения этой функции является вся координатная плоскость Oxy. Областью значений – промежуток
. Областью определения этой функции является вся координатная плоскость Oxy. Областью значений – промежуток  . Данная функция представляет собой Параболоид..
Определение
Линией уровня функции двух переменных
. Данная функция представляет собой Параболоид..
Определение
Линией уровня функции двух переменных  называется множество точек на плоскости, таких, что во всех этих точках значение функции одно и то же и равно C.
Пусть функция
называется множество точек на плоскости, таких, что во всех этих точках значение функции одно и то же и равно C.
Пусть функция  . Возьмем точку
. Возьмем точку  , любая e–окрестность которой содержит точки множества
, любая e–окрестность которой содержит точки множества  .
Определение
Функция
.
Определение
Функция  называется Непрерывной в точке А, если предел функции в этой точке Существует и Равен значению функции в этой точке:
называется Непрерывной в точке А, если предел функции в этой точке Существует и Равен значению функции в этой точке:
 .
Определение
Функция
.
Определение
Функция 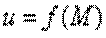 называется Непрерывной на множестве
называется Непрерывной на множестве  , если она непрерывна в любой точке этого множества.
Точки, в которых функция не обладает свойством непрерывности, называются Точками разрыва.
, если она непрерывна в любой точке этого множества.
Точки, в которых функция не обладает свойством непрерывности, называются Точками разрыва.



