

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Дифференциальные уравнения высшего порядка, допускающие понижение степени.
| |  Уравнение вида Уравнение вида  .
Общее решение уравнения вида .
Общее решение уравнения вида
 (13)
Получается путем (13)
Получается путем  - кратного интегрирования правой части исходного уравнения: - кратного интегрирования правой части исходного уравнения:
 .
Уравнение вида .
Уравнение вида  .
Данное уравнение не содержит явно искомую функцию .
Данное уравнение не содержит явно искомую функцию  и её производные до и её производные до  -го порядка включительно. С помощью замены -го порядка включительно. С помощью замены 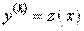 , где , где  - новая неизвестная функция, порядок уравнения может быть понижен на - новая неизвестная функция, порядок уравнения может быть понижен на  единиц. Действительно, в силу замены: единиц. Действительно, в силу замены:  . Следовательно, после подстановки значений производных в исходное уравнение получим уравнение . Следовательно, после подстановки значений производных в исходное уравнение получим уравнение  -го порядка: -го порядка:
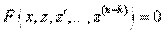 .
Предположим, что полученное уравнение мы можем решить, и его общее решение имеет вид: .
Предположим, что полученное уравнение мы можем решить, и его общее решение имеет вид:
 .
Тогда искомую функцию .
Тогда искомую функцию  находим из уравнения находим из уравнения
 ,
Которое является уравнением вида (13).
Уравнение вида ,
Которое является уравнением вида (13).
Уравнение вида  .
Данное уравнение не содержит явно независимую переменную .
Данное уравнение не содержит явно независимую переменную  . С помощью замены . С помощью замены  , где , где 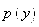 - новая неизвестная функция, порядок уравнения может быть понижен на единицу. Действительно, в силу замены: - новая неизвестная функция, порядок уравнения может быть понижен на единицу. Действительно, в силу замены: 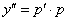 , ,  и т. д. Следовательно, после подстановки значений производных в исходное уравнение и т. д. Следовательно, после подстановки значений производных в исходное уравнение  -го порядка -го порядка
 .
Предположим, что полученное уравнение мы можем решить, и его общее решение имеет вид: .
Предположим, что полученное уравнение мы можем решить, и его общее решение имеет вид:
 .
Тогда искомую функцию .
Тогда искомую функцию  находим из уравнения находим из уравнения
 ,
Которое является уравнением с разделяющимися переменными.
Задание 1. Найти решение уравнения: ,
Которое является уравнением с разделяющимися переменными.
Задание 1. Найти решение уравнения:  .
Решение. Общее решение данного уравнения может быть получено в результате 2- кратного интегрирования правой части уравнения. Имеем: .
Решение. Общее решение данного уравнения может быть получено в результате 2- кратного интегрирования правой части уравнения. Имеем:
 .
И далее .
И далее

| | | Дифференциальные уравнения, допускающие понижение порядка
| В общем случае дифференциальное уравнение второго порядка можно записать в виде
 где F − заданная функция указанных аргументов. Если дифференциальное уравнение можно разрешить относительно второй производной y'', то его можно представить в следующем явном виде:
где F − заданная функция указанных аргументов. Если дифференциальное уравнение можно разрешить относительно второй производной y'', то его можно представить в следующем явном виде:
 В частных случаях функция f в правой части может содержать лишь одну или две переменных. Такие неполные уравнения включают в себя 5 различных типов:
В частных случаях функция f в правой части может содержать лишь одну или две переменных. Такие неполные уравнения включают в себя 5 различных типов:
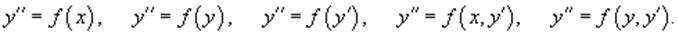 С помощью определенных подстановок эти уравнения можно преобразовать в уравнения первого порядка. В случае произвольных дифференциальных уравнений второго порядка, их порядок можно понизить, если эти уравнения обладают определенной симметрией. Ниже мы обсудим 2 типа таких уравнений (случаи 6 и 7):
· Функция F (x, y, y', y'') является однородной функцией аргументов y, y', y'';
· Функция F (x, y, y', y'') является точной производной функции первого порядка Ф (x, y, y').
Итак, рассмотрим указанные случаи понижения порядка более подробно.
Случай 1. Уравнение вида y''= f (x)
Если дано уравнение y'' = f (x), то его порядок можно понизить введением новой функции p (x), такой, что y' = p (x). В результате мы получим дифференциальное уравнение первого порядка
С помощью определенных подстановок эти уравнения можно преобразовать в уравнения первого порядка. В случае произвольных дифференциальных уравнений второго порядка, их порядок можно понизить, если эти уравнения обладают определенной симметрией. Ниже мы обсудим 2 типа таких уравнений (случаи 6 и 7):
· Функция F (x, y, y', y'') является однородной функцией аргументов y, y', y'';
· Функция F (x, y, y', y'') является точной производной функции первого порядка Ф (x, y, y').
Итак, рассмотрим указанные случаи понижения порядка более подробно.
Случай 1. Уравнение вида y''= f (x)
Если дано уравнение y'' = f (x), то его порядок можно понизить введением новой функции p (x), такой, что y' = p (x). В результате мы получим дифференциальное уравнение первого порядка
 Решая его, находим функцию p (x). Затем решаем второе уравнение
Решая его, находим функцию p (x). Затем решаем второе уравнение
 и получаем общее решение исходного уравнения.
Случай 2. Уравнение вида y''= f (y)
Здесь правая часть уравнения зависит только от переменной y. Вводим новую функцию p (y), полагая y' = p (y). Тогда можно записать:
и получаем общее решение исходного уравнения.
Случай 2. Уравнение вида y''= f (y)
Здесь правая часть уравнения зависит только от переменной y. Вводим новую функцию p (y), полагая y' = p (y). Тогда можно записать:
 и уравнение принимает вид:
и уравнение принимает вид:
 Решая его, находим функцию p (y). Затем находим решение уравнения y' = p (y), то есть функцию y (x).
Случай 3. Уравнение вида y''= f (y' )
В данном случае для понижения порядка вводим функцию y' = p (x) и получаем уравнение
Решая его, находим функцию p (y). Затем находим решение уравнения y' = p (y), то есть функцию y (x).
Случай 3. Уравнение вида y''= f (y' )
В данном случае для понижения порядка вводим функцию y' = p (x) и получаем уравнение
 которое является уравнением первого порядка с разделяющимися переменными p и x. Интегрируя, находим функцию p (x) и затем функцию y (x).
Случай 4. Уравнение вида y''= f (x, y' )
Используем подстановку y' = p (x), где p (x) − новая неизвестная функция, и получаем уравнение первого порядка
которое является уравнением первого порядка с разделяющимися переменными p и x. Интегрируя, находим функцию p (x) и затем функцию y (x).
Случай 4. Уравнение вида y''= f (x, y' )
Используем подстановку y' = p (x), где p (x) − новая неизвестная функция, и получаем уравнение первого порядка
 Интегрируя, определяем функцию p (x). Далее решаем еще одно уравнение 1-го порядка
и находим общее решение y (x).
Случай 5. Уравнение вида y''= f (y,y' )
Для решения такого уравнения, также как и в случае 2, вводим новую функцию p (y), полагая y' = p (y). Дифференцирование этого равенства по x приводит к уравнению
Интегрируя, определяем функцию p (x). Далее решаем еще одно уравнение 1-го порядка
и находим общее решение y (x).
Случай 5. Уравнение вида y''= f (y,y' )
Для решения такого уравнения, также как и в случае 2, вводим новую функцию p (y), полагая y' = p (y). Дифференцирование этого равенства по x приводит к уравнению
 В результате наше исходное уравнение записывается в виде уравнения 1-го порядка
В результате наше исходное уравнение записывается в виде уравнения 1-го порядка
 Решая его, находим функцию p (y). Затем решаем еще одно уравнение первого порядка
Решая его, находим функцию p (y). Затем решаем еще одно уравнение первого порядка
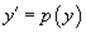 и определяем общее решение y (x). Рассмотренные 5 случаев понижения порядка не являются независимыми. Исходя из структуры уравнений, ясно, что случай 2 следует из случая 5, а случай 3 вытекает из более общего случая 4.
Случай 6. Функция F(x, y, y', y'') является однородной функцией аргументов y, y', y''
Если левая часть дифференциального уравнения
и определяем общее решение y (x). Рассмотренные 5 случаев понижения порядка не являются независимыми. Исходя из структуры уравнений, ясно, что случай 2 следует из случая 5, а случай 3 вытекает из более общего случая 4.
Случай 6. Функция F(x, y, y', y'') является однородной функцией аргументов y, y', y''
Если левая часть дифференциального уравнения
 удовлетворяет условию однородности, т.е. для любого k справедливо соотношение
удовлетворяет условию однородности, т.е. для любого k справедливо соотношение
 то порядок уравнения можно понизить с помощью подстановки
то порядок уравнения можно понизить с помощью подстановки
 После нахождения функции z (x) исходная функция y (x) находится интегрированием по формуле
После нахождения функции z (x) исходная функция y (x) находится интегрированием по формуле
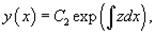 где C 2− постоянная интегрирования.
Случай 7. Функция F(x, y, y', y'') является точной производной
Если удается найти такую функцию Ф (x, y, y'), не содержащую второй производной y'' и удовлетворяющую равенству
где C 2− постоянная интегрирования.
Случай 7. Функция F(x, y, y', y'') является точной производной
Если удается найти такую функцию Ф (x, y, y'), не содержащую второй производной y'' и удовлетворяющую равенству
 то решение исходного уравнения представляется интегралом
то решение исходного уравнения представляется интегралом 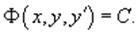 Таким образом уравнение второго порядка можно привести к уравнению первого порядка. В некоторых случаях левую часть исходного уравнения можно преобразовать в точную производную, используя интегрирующий множитель.
Таким образом уравнение второго порядка можно привести к уравнению первого порядка. В некоторых случаях левую часть исходного уравнения можно преобразовать в точную производную, используя интегрирующий множитель.
| | | | |
|



 Уравнение вида
Уравнение вида  .
Общее решение уравнения вида
.
Общее решение уравнения вида
 (13)
Получается путем
(13)
Получается путем  - кратного интегрирования правой части исходного уравнения:
- кратного интегрирования правой части исходного уравнения:
 .
Уравнение вида
.
Уравнение вида  .
Данное уравнение не содержит явно искомую функцию
.
Данное уравнение не содержит явно искомую функцию  и её производные до
и её производные до  -го порядка включительно. С помощью замены
-го порядка включительно. С помощью замены 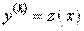 , где
, где  - новая неизвестная функция, порядок уравнения может быть понижен на
- новая неизвестная функция, порядок уравнения может быть понижен на  единиц. Действительно, в силу замены:
единиц. Действительно, в силу замены:  . Следовательно, после подстановки значений производных в исходное уравнение получим уравнение
. Следовательно, после подстановки значений производных в исходное уравнение получим уравнение  -го порядка:
-го порядка:
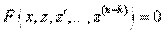 .
Предположим, что полученное уравнение мы можем решить, и его общее решение имеет вид:
.
Предположим, что полученное уравнение мы можем решить, и его общее решение имеет вид:
 .
Тогда искомую функцию
.
Тогда искомую функцию  находим из уравнения
находим из уравнения
 ,
Которое является уравнением вида (13).
Уравнение вида
,
Которое является уравнением вида (13).
Уравнение вида  .
Данное уравнение не содержит явно независимую переменную
.
Данное уравнение не содержит явно независимую переменную  . С помощью замены
. С помощью замены  , где
, где 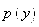 - новая неизвестная функция, порядок уравнения может быть понижен на единицу. Действительно, в силу замены:
- новая неизвестная функция, порядок уравнения может быть понижен на единицу. Действительно, в силу замены: 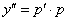 ,
,  и т. д. Следовательно, после подстановки значений производных в исходное уравнение
и т. д. Следовательно, после подстановки значений производных в исходное уравнение  -го порядка
-го порядка
 .
Предположим, что полученное уравнение мы можем решить, и его общее решение имеет вид:
.
Предположим, что полученное уравнение мы можем решить, и его общее решение имеет вид:
 .
Тогда искомую функцию
.
Тогда искомую функцию  ,
Которое является уравнением с разделяющимися переменными.
Задание 1. Найти решение уравнения:
,
Которое является уравнением с разделяющимися переменными.
Задание 1. Найти решение уравнения:  .
Решение. Общее решение данного уравнения может быть получено в результате 2- кратного интегрирования правой части уравнения. Имеем:
.
Решение. Общее решение данного уравнения может быть получено в результате 2- кратного интегрирования правой части уравнения. Имеем:
 .
И далее
.
И далее

 где F − заданная функция указанных аргументов. Если дифференциальное уравнение можно разрешить относительно второй производной y'', то его можно представить в следующем явном виде:
где F − заданная функция указанных аргументов. Если дифференциальное уравнение можно разрешить относительно второй производной y'', то его можно представить в следующем явном виде:
 В частных случаях функция f в правой части может содержать лишь одну или две переменных. Такие неполные уравнения включают в себя 5 различных типов:
В частных случаях функция f в правой части может содержать лишь одну или две переменных. Такие неполные уравнения включают в себя 5 различных типов:
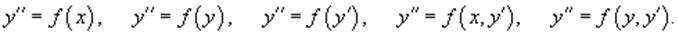 С помощью определенных подстановок эти уравнения можно преобразовать в уравнения первого порядка. В случае произвольных дифференциальных уравнений второго порядка, их порядок можно понизить, если эти уравнения обладают определенной симметрией. Ниже мы обсудим 2 типа таких уравнений (случаи 6 и 7):
· Функция F (x, y, y', y'') является однородной функцией аргументов y, y', y'';
· Функция F (x, y, y', y'') является точной производной функции первого порядка Ф (x, y, y').
Итак, рассмотрим указанные случаи понижения порядка более подробно.
Случай 1. Уравнение вида y''= f (x)
Если дано уравнение y'' = f (x), то его порядок можно понизить введением новой функции p (x), такой, что y' = p (x). В результате мы получим дифференциальное уравнение первого порядка
С помощью определенных подстановок эти уравнения можно преобразовать в уравнения первого порядка. В случае произвольных дифференциальных уравнений второго порядка, их порядок можно понизить, если эти уравнения обладают определенной симметрией. Ниже мы обсудим 2 типа таких уравнений (случаи 6 и 7):
· Функция F (x, y, y', y'') является однородной функцией аргументов y, y', y'';
· Функция F (x, y, y', y'') является точной производной функции первого порядка Ф (x, y, y').
Итак, рассмотрим указанные случаи понижения порядка более подробно.
Случай 1. Уравнение вида y''= f (x)
Если дано уравнение y'' = f (x), то его порядок можно понизить введением новой функции p (x), такой, что y' = p (x). В результате мы получим дифференциальное уравнение первого порядка
 Решая его, находим функцию p (x). Затем решаем второе уравнение
Решая его, находим функцию p (x). Затем решаем второе уравнение
 и получаем общее решение исходного уравнения.
Случай 2. Уравнение вида y''= f (y)
Здесь правая часть уравнения зависит только от переменной y. Вводим новую функцию p (y), полагая y' = p (y). Тогда можно записать:
и получаем общее решение исходного уравнения.
Случай 2. Уравнение вида y''= f (y)
Здесь правая часть уравнения зависит только от переменной y. Вводим новую функцию p (y), полагая y' = p (y). Тогда можно записать:
 и уравнение принимает вид:
и уравнение принимает вид:
 Решая его, находим функцию p (y). Затем находим решение уравнения y' = p (y), то есть функцию y (x).
Случай 3. Уравнение вида y''= f (y' )
В данном случае для понижения порядка вводим функцию y' = p (x) и получаем уравнение
Решая его, находим функцию p (y). Затем находим решение уравнения y' = p (y), то есть функцию y (x).
Случай 3. Уравнение вида y''= f (y' )
В данном случае для понижения порядка вводим функцию y' = p (x) и получаем уравнение
 которое является уравнением первого порядка с разделяющимися переменными p и x. Интегрируя, находим функцию p (x) и затем функцию y (x).
Случай 4. Уравнение вида y''= f (x, y' )
Используем подстановку y' = p (x), где p (x) − новая неизвестная функция, и получаем уравнение первого порядка
которое является уравнением первого порядка с разделяющимися переменными p и x. Интегрируя, находим функцию p (x) и затем функцию y (x).
Случай 4. Уравнение вида y''= f (x, y' )
Используем подстановку y' = p (x), где p (x) − новая неизвестная функция, и получаем уравнение первого порядка
 Интегрируя, определяем функцию p (x). Далее решаем еще одно уравнение 1-го порядка
и находим общее решение y (x).
Случай 5. Уравнение вида y''= f (y,y' )
Для решения такого уравнения, также как и в случае 2, вводим новую функцию p (y), полагая y' = p (y). Дифференцирование этого равенства по x приводит к уравнению
Интегрируя, определяем функцию p (x). Далее решаем еще одно уравнение 1-го порядка
и находим общее решение y (x).
Случай 5. Уравнение вида y''= f (y,y' )
Для решения такого уравнения, также как и в случае 2, вводим новую функцию p (y), полагая y' = p (y). Дифференцирование этого равенства по x приводит к уравнению
 В результате наше исходное уравнение записывается в виде уравнения 1-го порядка
В результате наше исходное уравнение записывается в виде уравнения 1-го порядка
 Решая его, находим функцию p (y). Затем решаем еще одно уравнение первого порядка
Решая его, находим функцию p (y). Затем решаем еще одно уравнение первого порядка
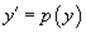 и определяем общее решение y (x). Рассмотренные 5 случаев понижения порядка не являются независимыми. Исходя из структуры уравнений, ясно, что случай 2 следует из случая 5, а случай 3 вытекает из более общего случая 4.
Случай 6. Функция F(x, y, y', y'') является однородной функцией аргументов y, y', y''
Если левая часть дифференциального уравнения
и определяем общее решение y (x). Рассмотренные 5 случаев понижения порядка не являются независимыми. Исходя из структуры уравнений, ясно, что случай 2 следует из случая 5, а случай 3 вытекает из более общего случая 4.
Случай 6. Функция F(x, y, y', y'') является однородной функцией аргументов y, y', y''
Если левая часть дифференциального уравнения
 удовлетворяет условию однородности, т.е. для любого k справедливо соотношение
удовлетворяет условию однородности, т.е. для любого k справедливо соотношение
 то порядок уравнения можно понизить с помощью подстановки
то порядок уравнения можно понизить с помощью подстановки
 После нахождения функции z (x) исходная функция y (x) находится интегрированием по формуле
После нахождения функции z (x) исходная функция y (x) находится интегрированием по формуле
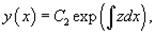 где C 2− постоянная интегрирования.
Случай 7. Функция F(x, y, y', y'') является точной производной
Если удается найти такую функцию Ф (x, y, y'), не содержащую второй производной y'' и удовлетворяющую равенству
где C 2− постоянная интегрирования.
Случай 7. Функция F(x, y, y', y'') является точной производной
Если удается найти такую функцию Ф (x, y, y'), не содержащую второй производной y'' и удовлетворяющую равенству
 то решение исходного уравнения представляется интегралом
то решение исходного уравнения представляется интегралом 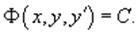 Таким образом уравнение второго порядка можно привести к уравнению первого порядка. В некоторых случаях левую часть исходного уравнения можно преобразовать в точную производную, используя интегрирующий множитель.
Таким образом уравнение второго порядка можно привести к уравнению первого порядка. В некоторых случаях левую часть исходного уравнения можно преобразовать в точную производную, используя интегрирующий множитель.



