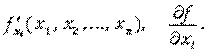Рассмотрим изменение функции
 При задании приращения только одному из ее аргументов – ХI, и назовем его
При задании приращения только одному из ее аргументов – ХI, и назовем его 
Обозначения:
Замечание. При практическом вычислении частных производных пользуемся обычными правилами дифференцирования функции одной переменной, полагая аргумент, по которому ведется дифференцирование, переменным, а остальные аргументы – постоянными. Примеры.
|
| Дифференциал. Производные сложных функций | 
| 
| 
|
Частные производные и дифференциал
Частной производной функции 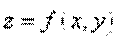 по переменной
по переменной  В точке
В точке  называется предел:
называется предел:
 , (3)
, (3)
Где 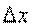 - приращение аргумента
- приращение аргумента  . Аналогично определяется Частная производная функции
. Аналогично определяется Частная производная функции  по Переменной
по Переменной 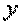 в точке
в точке  :
:
 , (4)
, (4)
Где 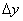 - приращение аргумента
- приращение аргумента  . Частные производные функции
. Частные производные функции  по переменной
по переменной  обозначают различными способами, например:
обозначают различными способами, например:
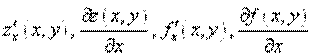
Аналогично частные производные функции  по переменной
по переменной  обозначают следующим образом:
обозначают следующим образом:

Частные производные.
Пусть z=f(x,y). Зафиксируем какую-либо точку (x,y), а затем, не меняя закрепленного значения аргумента y, придадим аргументу x приращение  . Тогда z получит приращение, которое называется частным приращением z по x и обозначается
. Тогда z получит приращение, которое называется частным приращением z по x и обозначается  и определяется формулой
и определяется формулой 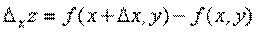 .
.
Аналогично, если x сохраняет постоянное значение, а y получает приращение 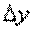 , то z получает частное приращение z по y,
, то z получает частное приращение z по y,  .
.
Определение. Частной производной по x от функции z=f(x,y) называется предел отношения частного приращения  по x к приращению
по x к приращению  при стремлении
при стремлении  к нулю, т.е.
к нулю, т.е. 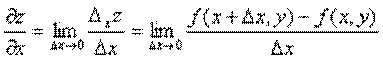
Частная производная обозначается одним из символов  .
.
Аналогично определяется частная производная по y:
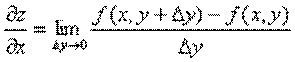 .
.
Таким образом, частные производные функции двух переменных вычисляются по тем же правилам, что и производные функции одного переменного.
Пример. Найти частные производные функции z=x2e x-2y.
Решение.
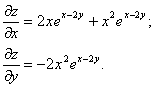
Частные производные функции любого числа переменных определяются аналогично
Дифференцируемость ФНП
Пусть функция z(f,y) дифференцируема по x и y.
Приращение функции 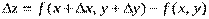 называют полным приращением.
называют полным приращением.
Полное приращение функции весьма сложно выражается через приращения независимых переменных D x, D y. Можно показать, что
 , где
, где  .
.
Сумма 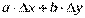 называется полным дифференциалом функции z=f(x,y).
называется полным дифференциалом функции z=f(x,y).
Определение: полным дифференциалом функции двух независимых
переменных называется главная часть полного приращения
функции, линейная относительно приращений независимых
переменных.
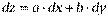 , D x=dx, D y=dy (1)
, D x=dx, D y=dy (1)
Теорема: полный дифференциал функции двух независимых переменных равен
сумме произведений частных производных функции на дифференциалы
соответствующих независимых переменных.
Доказательство:
Формула (1) справедлива при произвольных dx и dy. В частности, при dy =0:

Аналогично доказывается, что 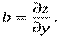
Тогда 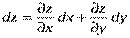 или
или 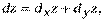
то есть дифференциал функции двух независимых переменных равен сумме ее частных дифференциалов.
Определение: функция двух независимых переменных, имеющая в некоторой
точке дифференциал, называется дифференцируемой в этой точке.
Теорема: если функция z=f(x,y) имеет в точке P(x,y) непрерывные частные
производные 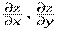 , то в этой точке функция дифференцируема.
, то в этой точке функция дифференцируема.
|
| Поделиться: |



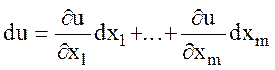 ,
,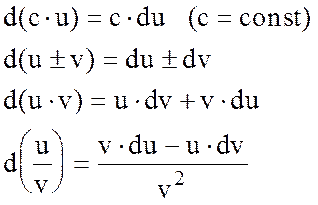
 ,
,
 (16.4.2) можно записать в виде
(16.4.2) можно записать в виде .
.
 называется Дифференцируемой в точке
называется Дифференцируемой в точке 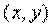 , если ее полное приращение может быть представлено в виде
, если ее полное приращение может быть представлено в виде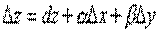
 – дифференциал функции,
– дифференциал функции, 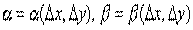 – бесконечно малые при
– бесконечно малые при  .
. , часть полного приращения функции.
, часть полного приращения функции.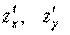 существуют в окрестности точки
существуют в окрестности точки 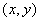 и непрерывны в самой точке
и непрерывны в самой точке  Дифференцируема В этой точке.
Дифференцируема В этой точке.