
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точки разрыва функции и их классификацияСодержание книги
Поиск на нашем сайте Если ф-ияf(x)непрерывна в т.x0, то limf(x)=f(x0). А это означает, что f(x0-0)=f(x0+0)=f(x0) (*) x→x0 Если выполняется рав-во (*), то x0-т.непрерывности ф-ии. Опр.1-точкой разрыва ф-ииf(x)наз-ся т., в кот.f(x) не явл-сянепрерывной. В т.разрыва ф-ии хотя бы одно из двух рав-в (*) должно нарушаться. Точки разрыва делятся на два вида: т.разрываIрода и II рода. Опр.2-т. x0наз-сят.разрываI рода, если в т.x0 оба односторонних предела f(x0-0) и f(x0+0)сущ-ют и конечны В свою очередь, т.разрываI рода делятся на т.устранимого разрыва и на т.неустранимого разрыва. Опр.3 – т. разрыва I рода наз-сят.устранимого разрыва, если f(x0-0)=f(x0+0). Но при этом f(x) либо не опр-на в т.x0, либо опр-на в т.x0, но f(x0)≠f(x0-0). Опр.4 – т. разрыва Iрода наз-сят.неустранимого разрыва, если f(x0-0)≠f(x0+0). При этом число hx0=f(x0+0)-f(x0-0) – наз-ся скачком ф-ии. Опр.5 – т.разрываII рода наз-ся т., в кот. хотя бы один из односторонних пределов либо не сущ-ет, либо бесконечен.
24 Предельный переход под знаком непрерывной функции. Раскрытие неопределенностей вида
25 Производная функции. Геометрический, механический, экономический смысл производной Опр. 1 Производной функции y = f(x) в точке 26 Непрерывность функции, имеющий производную. Если f(x)диф-на в точке
27 Правила дифференцирования: дифференцирование суммы, произведения, частного; производная обратной и сложной функции; производные элементарных функцийТ1. Пусть ф-ции U(x) и V(x) диф-мы в точке 28 Логарифмическая производная, производная неявной функции. Производная функции, заданной параметрически Логарифмическая производная – производная от натурального логарифма модуля (абсолютной величины) – данной функции: Используя формулу производной сложной функции, найдем, что
29 Касательная нормаль к графику функции. опр1:Нормалью к гр.ф-ции y=f(x) в (.) 30. Дифференциал ф-ции,его геометрический смысл.приближенные вычисления с помощью дифференциала. Опр.1- ф-ияy=f(x) наз-сядиф-мой в т.x0, если её приращение м.б. представлено в виде ∆y(x0)=A. ∆x+α(∆x)∙∆x., где α(∆x)→0 при ∆x→0. Число А не зависит от ∆x. Можно показать, что если ф-ия в т.x0 имеет конечную производную в т.x0, то A=y'(x0). Опр.2-дифференциалом ф-ииy=f(x) в т.x0наз-ся главная линейная по ∆x часть приращения ф-ии, и обозначается dy(x0)=A∙∆x=y'(x0)∙∆x. Если y=x, то y'(x)=x'x=1. dy(x)=y'(x)∙∆x. dx=1∙∆x – для независимой переменной xдифф-л и приращение совпадают. dy(x0)=y'(x0)∙dx. dy(x)=y'(x)dx. - Формулы для вычисления диф-ла ф-ии Геометрич. смысл диф-ла: ∆M0LK: KL/M0K=KL/∆x=y'(x0) KL=y'(x0)∙∆=dy(x0).Dy(x0)=KL-приращение ординаты касательной к графику ф-ииy=f(x), когда аргумент xполучает приращение ∆x. ∆y(x0)=MK-приращение ординаты кривой. dy(x0)=KL-приращение ординаты касательной. Приближённые вычисления с помощью диф-ла. Т.к. в правой части формулы оба слагаемых стремятся к 0 и второй слагаемое стремится к 0 быстрее первого, то вторым слагаемым пренебрегают при проведении приближённых вычислений. Приближённо считают приращение ф-ии совпадающим с диф-лом. ∆y(x0)≈dy(x0) ∆y(x0)≈y'(x0)∙∆x. -формулы для вычисления приближённого значения приращения ф-ии. ∆y(x0)=y(x0+∆x)-y(x0)≈y'(x0)∙∆x. y(x0+∆x)≈y(x0)+y'(x0)∙∆x – формула для вычисления приближённого значения ф-ии. 31. Производные и дифференциалы высшего порядка Пусть функция y = f (x) дифференцируема на некотором отрезке [ a, b ]. Значения производной f'(x) зависят от х, т.е. производная f'(x) тоже представляет собой некоторую функцию от х. Дифференцируя эту функцию, мы получаем производную от производной. О. Производная от первой производной называется производной второго порядка или второй производной. Обозначается y''=(f'(x))'= f''(x). Физический смысл второй производной: вторая производная f''(x) равна скорости изменения скорости, т.е. ускорению движущейся точки в момент времени х. Вторая производная также может быть функцией, определенной на некотором множестве. Если эта функция имеет производную, то эта производная называется третьей производной функции f(x) и обозначается f'''(x). О. Если определена (n -1) -я производная f (n -1) (x) и существует её производная, то она называется n-й производной функции f(x): f (n) (x) = (f (n -1) (x))'. Все производные, начиная со второй, называются производными высших порядков. Функцию, имеющую на данном множестве конечную производную порядка n, называют n раз дифференцируемой на данном множестве. Дифференциал функции y = f (x) выражается в виде dy = f'(x) dx. Тогда, если он является некоторой функцией от х, то справедливо следующее: О. Дифференциал от дифференциала функции называется дифференциалом второго порядка или вторым дифференциалом: d 2 y = f ''(x) dx 2 . О. Дифференциал от дифференциала n -го порядка называется дифференциалом (n +1)-го порядка. Правило Лопиталя Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

 ….с помощью алгебраических преобразований, первого и второго замечательных пределов, использования эквивалентных бесконечно малых функций. Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:
….с помощью алгебраических преобразований, первого и второго замечательных пределов, использования эквивалентных бесконечно малых функций. Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:  пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.
пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.  Для раскрытия неопределённостей типа
Для раскрытия неопределённостей типа  используется следующий алгоритм: Выявление старшей степени переменной; Деление на эту переменную как числителя, так и знаменателя. Для раскрытия неопределённостей типа
используется следующий алгоритм: Выявление старшей степени переменной; Деление на эту переменную как числителя, так и знаменателя. Для раскрытия неопределённостей типа  существует следующий алгоритм: Разложение на множители числителя и знаменателя; Сокращение дроби. Для раскрытия неопределённостей типа
существует следующий алгоритм: Разложение на множители числителя и знаменателя; Сокращение дроби. Для раскрытия неопределённостей типа  иногда удобно применить следующее преобразование:Пусть
иногда удобно применить следующее преобразование:Пусть 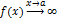 и
и 
 Первый и второй замечательный предел Для раскрытия неопределенностей, содержащих тригонометрические функции, используют первый замечательный предел Первый замечательный предел
Первый и второй замечательный предел Для раскрытия неопределенностей, содержащих тригонометрические функции, используют первый замечательный предел Первый замечательный предел  Данный предел относят обычно к неопределенностям вида 1∞. Раскрытие подобных неопределенностей как правило, связано с использованием второго замечательного предела Второй замечательные предел
Данный предел относят обычно к неопределенностям вида 1∞. Раскрытие подобных неопределенностей как правило, связано с использованием второго замечательного предела Второй замечательные предел  Второй замечательный предел существует. Его значение -- число, лежащее между
Второй замечательный предел существует. Его значение -- число, лежащее между  и 3. Более подробное изучение числа Е показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:
и 3. Более подробное изучение числа Е показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:  Точка x0, в которой нарушено хотя бы одно из трех условий непрерывности функции, называется точкой разрыва функции. Если в точке x0 существуют конечные пределы f(x0-0) и f(x0+0), такие, что f(x0-0)≠f(x0+0), то x0 называется точкой разрыва первого рода. Если хотя бы один из пределов f(x0-0) и f(x0+0) не существует или равен бесконечности, то точку x0 называют точкой разрыва второго рода. Если f(x0-0)=f(x0+0) и функция f(x) не определена в точке x0 или определена, но f(x)≠f(x0-0)=f(x0+0), то точку x0 называют устранимой точкой разрыва функции. Использования эквивалентных бесконечно малых функций. Бесконечно малые функции обладают следующими свойствами: 1) Алгебраическая сумма любого конечного числа бесконечно малых в некоторой точке функций есть функция, бесконечно малая в той же точке. 2) Произведение любого конечного числа бесконечно малых в некоторой точке функций есть функция, бесконечно малая в той же точке. 3) Произведение бесконечно малой в некоторой точке функции на функцию ограниченную есть функция, бесконечно малая в той же точке. Бесконечно малые в некоторой точке х0 функции a (x) и b (x) называются бесконечно малыми одного порядка Предел частного (отношения) двух бесконечно малых величин не изменится, если одну из них (или обе) заменить эквивалентной величиной.
Точка x0, в которой нарушено хотя бы одно из трех условий непрерывности функции, называется точкой разрыва функции. Если в точке x0 существуют конечные пределы f(x0-0) и f(x0+0), такие, что f(x0-0)≠f(x0+0), то x0 называется точкой разрыва первого рода. Если хотя бы один из пределов f(x0-0) и f(x0+0) не существует или равен бесконечности, то точку x0 называют точкой разрыва второго рода. Если f(x0-0)=f(x0+0) и функция f(x) не определена в точке x0 или определена, но f(x)≠f(x0-0)=f(x0+0), то точку x0 называют устранимой точкой разрыва функции. Использования эквивалентных бесконечно малых функций. Бесконечно малые функции обладают следующими свойствами: 1) Алгебраическая сумма любого конечного числа бесконечно малых в некоторой точке функций есть функция, бесконечно малая в той же точке. 2) Произведение любого конечного числа бесконечно малых в некоторой точке функций есть функция, бесконечно малая в той же точке. 3) Произведение бесконечно малой в некоторой точке функции на функцию ограниченную есть функция, бесконечно малая в той же точке. Бесконечно малые в некоторой точке х0 функции a (x) и b (x) называются бесконечно малыми одного порядка Предел частного (отношения) двух бесконечно малых величин не изменится, если одну из них (или обе) заменить эквивалентной величиной. н-ся предел отношения приращения функции
н-ся предел отношения приращения функции  , приращения аргумента
, приращения аргумента  ,когда
,когда  .Опр2.Ф-ция y=f(x) н-ся дифференцируемой в точке
.Опр2.Ф-ция y=f(x) н-ся дифференцируемой в точке  предел существует и конечен. Если предел в этой формуле не существует или бесконечен,тогда f(x) не дифференцируемый, в точке
предел существует и конечен. Если предел в этой формуле не существует или бесконечен,тогда f(x) не дифференцируемый, в точке  -мгновенная скорость изменения ф-ции в точке; Опр3.Касательная к графику ф-ции в точке пересечения(
-мгновенная скорость изменения ф-ции в точке; Опр3.Касательная к графику ф-ции в точке пересечения(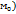 предельное положение секущей, когда т М стремится к
предельное положение секущей, когда т М стремится к 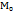 по графику ф-ции.. Геометрический смысл производной:
по графику ф-ции.. Геометрический смысл производной:  . Если f(x) ф-ция издержек,то
. Если f(x) ф-ция издержек,то  предельные издержки.
предельные издержки. -есть конечное число. По теореме из теории пределов, если предел
-есть конечное число. По теореме из теории пределов, если предел  то
то  где 𝓛(х)
где 𝓛(х)  , при х
, при х  , в роли
, в роли 
 , где
, где 
 при
при 
 ПРи
ПРи 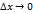 ,
,  По опр.непрерывности ф-ции на языке прирощений у(х) –непрерывно в точке
По опр.непрерывности ф-ции на языке прирощений у(х) –непрерывно в точке  ; 2)
; 2)  ;3)
;3) 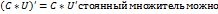 выносить за знак производной.4)
выносить за знак производной.4)  ; 5)
; 5)  . Т2.Производная сложной ф-ции.Пусть ф-ция y=F(U) диф-ма в точке
. Т2.Производная сложной ф-ции.Пусть ф-ция y=F(U) диф-ма в точке  ,а ф-ция U=
,а ф-ция U=  диф-мав точке
диф-мав точке  диф в точке
диф в точке 
 Т3.Производная обратной ф-ции.Пусть ф-ция f(x) диф в точке
Т3.Производная обратной ф-ции.Пусть ф-ция f(x) диф в точке  ,тогда обр ф-ция
,тогда обр ф-ция  диф-ма в точке f(
диф-ма в точке f( имеет место формула:
имеет место формула: 

 Логарифмическую производную используют, например, при дифференцировании (нахождении производной или дифференциала) степенно-показательной функции. Функция вида y = [u(x)]v(x) называется степенно – показательной. Для вычисления ее производной (при условии, что у' существует), нужно прологарифмировать функцию по любому основанию (обычно по основанию е). Затем нужно вычислить производную полученной неявной функции. Пример. Найти производную функции y = (sinx)x Логарифмируем функцию по основанию е:lny = x lnsinx. Дифференцируем обе части равенства по х, получаем
Логарифмическую производную используют, например, при дифференцировании (нахождении производной или дифференциала) степенно-показательной функции. Функция вида y = [u(x)]v(x) называется степенно – показательной. Для вычисления ее производной (при условии, что у' существует), нужно прологарифмировать функцию по любому основанию (обычно по основанию е). Затем нужно вычислить производную полученной неявной функции. Пример. Найти производную функции y = (sinx)x Логарифмируем функцию по основанию е:lny = x lnsinx. Дифференцируем обе части равенства по х, получаем  отсюда
отсюда  или
или  Рассмотренный прием называется логарифмическим дифференцированием. Он применяется не только для вычисления производных степенно-показательных функций, но и в случаях, когда аналитическое выражение функции содержит несколько множителей. Алгоритм вычисления производной y'(x) от неявной функции выглядит следующим образом: Сначала необходимо продифференцировать обе части уравнения по отношению к x, предполагая, что y - это дифференцируемая функция x и используя правило вычисления производной от сложной функции; Решить полученное уравнение относительно производной y'(x).
Рассмотренный прием называется логарифмическим дифференцированием. Он применяется не только для вычисления производных степенно-показательных функций, но и в случаях, когда аналитическое выражение функции содержит несколько множителей. Алгоритм вычисления производной y'(x) от неявной функции выглядит следующим образом: Сначала необходимо продифференцировать обе части уравнения по отношению к x, предполагая, что y - это дифференцируемая функция x и используя правило вычисления производной от сложной функции; Решить полученное уравнение относительно производной y'(x).  – пример неявной функции. Пусть задана зависимость двух переменных x и y от параметра t, изменяющегося в пределах от α до β:
– пример неявной функции. Пусть задана зависимость двух переменных x и y от параметра t, изменяющегося в пределах от α до β:  Пусть функция
Пусть функция  имеет обратную:
имеет обратную:  . Тогда мы можем, взяв композицию функций
. Тогда мы можем, взяв композицию функций  и
и  , получить зависимость y от x:
, получить зависимость y от x: 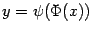 . Зависимость yвеличины от величины x, заданная через зависимость каждой из них от параметра t в виде
. Зависимость yвеличины от величины x, заданная через зависимость каждой из них от параметра t в виде  , называется функцией
, называется функцией  , заданной параметрически.Производную функции y(x), заданной параметрически, можно выразить через производные функций
, заданной параметрически.Производную функции y(x), заданной параметрически, можно выразить через производные функций  и
и  : поскольку
: поскольку  , то
, то  где
где  и x, снова выраженной в виде параметрической зависимости:
и x, снова выраженной в виде параметрической зависимости: 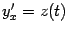 ,
,  ; второе из этих соотношений -- то же, что участвовало в параметрическом задании функции y(x). Несмотря на то, что производная не выражена через x в явном виде, это не мешает решать нам задачи, связанные с нахождением производной, найдя соответствующее значение параметра t.
; второе из этих соотношений -- то же, что участвовало в параметрическом задании функции y(x). Несмотря на то, что производная не выражена через x в явном виде, это не мешает решать нам задачи, связанные с нахождением производной, найдя соответствующее значение параметра t. наз прямая проходящая через(.)
наз прямая проходящая через(.)  необход и дост условие перпендикулярности двух прямых.
необход и дост условие перпендикулярности двух прямых.  -угл коэф касательной.
-угл коэф касательной.  -угл коэф нормали. Уравнение нормали:
-угл коэф нормали. Уравнение нормали: 
 или
или  . Пусть a является некоторым конечным действительным числом или равно бесконечности. Если
. Пусть a является некоторым конечным действительным числом или равно бесконечности. Если  и
и  , то
, то  ; если
; если  и
и  , то аналогично
, то аналогично  . Первые две неопределенности
. Первые две неопределенности  можно свести к типу
можно свести к типу  или
или  с помощью алгебраических преобразований. А неопределенности
с помощью алгебраических преобразований. А неопределенности  сводятся к типу
сводятся к типу  с помощью соотношения
с помощью соотношения 



