
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выделение целой части неправильной алгебраической дроби.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если числитель меньше знаменателя, такая дробь называется правильной. В противном случае (т.е. когда числитель больше или хотя бы равен знаменателю) дробь называется неправильной, и в ней можно выделить целую часть. Чтобы выделить целую часть в неправильной дроби, надо выполнить три простых шага: 1. Найдите, сколько раз знаменатель помещается в числителе. Другими словами, найдите максимальное целое число, которое при умножении на знаменатель все равно будет меньше числителя (в крайнем случае — равно). Это число и будет целой частью, поэтому записываем его спереди; 2. Умножьте знаменатель на целую часть, найденную в предыдущем шаге, а результат вычтите из числителя. Полученный «огрызок» называется остатком от деления, он всегда будет положительным (в крайнем случае — ноль). Записываем его в числитель новой дроби;3. Знаменатель переписываем без изменений.
50.Разложение правильной алгебраической дроби на простейшие. Опр.1-рацион. дробь наз-ся правильной, если степень многочлена числителя меньше степени многочлена знаменателя. Теорема. Всякую правильную рацион.дробь можно представить в виде суммы простейших дробей, причём единственным образом. Правильную часть рацион.дроби разложим на сумму простейших дробей. Вид разложения зависит от корней знаменателя. 1.Все корни знаменателя действит-е простые.таким образом, корням в разложении соответствуют дроби первого типа: Pn(x)/Qm(x)=Pn(x)/(x-a1)(x-a2)…(x-am)=A1/x-a1+A2/x-a2+…+Am/x-am. (n<m) 2.Среди действит. корней знаменателя есть кратные корни, кот-м соответствуют дроби первого и второго типа: PN(x)/Qm(x)=Pn(x)/(x-a1)k1(x-a2)k2(x-a3)…(x-ae)=Ak1/(x-a1)k1+Ak-1/(x-a1)k1-1+…+A2/(x-a1)2+A1/x-a1+Bk2/(x-a2)k2+Bk2-1/(x-a2)k2-1+…+B2/(x-a2)2+B1/(x-a2)+C/x-a3+…+D/x-ae. 3.Знаменатель содержит комплексно сопряжённые корни простые, кот.соответствуют дроби 3-го типа. Pn(x)/Qm(x)=Pn(x)/(x2+px+q)(x2+bx+c)(x-x1)…(x-xe)=Ax+B/x2+px+q + Cx+D/x2+bx+c + L/x-x1 +…+ M/x-xe. (n<m, D=p2-4q<0, D=b2-4c<0). 4. Знаменатель содержит кратные комплексно сопряжённые корни, кот.соответствуют дроби 3-го и 4-го типа. Pn(x)/Qm(x)=Pn(x)/(x2+px+q)k(x-x1)…(x-xe)=Akx+Bk/(x2+px+q)k+ Ak-1+Bk-1/(x2+px+q)k-1 +…+ A2x+B2/(x2+px+q)2 + A1x+B1/x2+px+q + C1/x-x1 +…+ Ce/x-xe. Замечание: коэф-ты разложения рпавильнойрацион.дроби на сумму простейших дробей находятся методом неопр-х коэф-тов. Для этого, правая часть разложения приводится к общему знаменателю и полученный числитель приравнивается к числителю исходной правильной дроби. Далее, уравниваются коэф-ты при одинаковых степенях x в левой и правой части рав-ва. Приравнивание коэф-тов начинается со степени xна 1 меньше степени знаменателя. В рез-теполучаетсясис-ма линейных ур-ий, кот.имеет единств. реш-е. Это реш-е в общем случае находится методом Гаусса.
51.Первообразная функция, неопределенный интеграл как множество первообразных, основные свойства неопределенных интегралов. Основная задача ДУ исчисление по заданной ф-ции, найти ее производную или диф-л 52.Таблица простейших интегралов. 1) 53.Основные методы интегрирования: алгебраические и тригонометрические преобразования подынтегральной функции, дифференциальное преобразование подынтегральной функции, замена переменной интегрирования, интегрирование по частям. 1.Непосредственноеинтегриров-е - под знаком интеграла проводим тождественные преобразов-я подинтегральной ф-ии. Используем св-во линейности неопр-го интеграла и таблицу неопр-х интегралов. 2.Интегриров-е подстановкой, замена переменной. Т 1. Пусть ф-ияf(x) непрерывна на отрезке [a,b], а ф-ияx=ϕ(t) нерперывна, имеет непрерывную производную на отрезке [α,β] и при t∈[α,β] x=ϕ(t)∈[a,b].Тогда справедлива фор-ла:∫f(x)dx= ⎸x=ϕ(t) ⎸=∫f(ϕ(t))∙ϕ'(t)dt. ⎸dx=ϕ'(t)dt⎸ Замечания: Эту формулу можно применять как слева направо, так и справа налево. 3.Интегриров-е по частям в неопр-м интеграле. Теорема. Пусть ф-ииU(x) и V(x)име.т непрерывные производные на интервале (a,b), тогда справедлива формула: ∫UdV=U∙V-∫V∙dU (*) Д-во: (UV)'=U'V+UV' (UV)'dx=(U'dx)V+U(V'dx) d(UV)=(dU)V+UdV ∫d(UV)=∫VdU+∫UdV UV=∫VdU+∫UdV ∫UdV=UV-∫VdU, что и треб.док-ть. Замечания: 1.При подборе Uи V интеграл в правой части фор-лы (*) должен быть более простого вида, чем интеграл в левой части этой фор-лы. 2.В кач-веU берём ф-ию, которую трудно интегрировать. 3.Если производная трансцендентной ф-ии снова явл-ся трансцендентной ф-ей, то за U берём алгебраич.ф-ию. 4.Если производная трансцендентной ф-ииявл-сяалгебраич.ф-ей, тогда за U берём трансцендентную ф-ию. Интегриров-е по частям применяется столько раз, какова степень многочлена Pn(x).После применения фор-лыинтегриров-я по частям в правой части получается интеграл, в подынтегральной ф-ии которого надо провести тождественные преобразов-я и получить ур-е относительно исходного интеграла, затем решить это ур-е и найти неопр-ый интеграл.
54. Интегрирование рациональных дробей. Рациональной дробью называется функция R(x), представленная в виде R(x)= 55. Интегрирование тригонометрических функций. Интегралы вида: òf(sinx)cosxdx, òf(cosx)sinxdx, ò 56.Интегрирование иррациональных функций. Некоторые типы интегралов от алгебраических иррациональностей надлежащей заменой переменных могут быть сведены к интегралам от рациональных функций. Такое преобразование интеграла называется его рационализацией. Для интегрирования рациональной функции
57.Определенный интеграл, основные свойства, геометрический смысл. Определенным интегралом от a до b непрерывной функции y=f(x), определенной на интервале [a;b], называется прирощение первообразной F(x) для этой функции, то есть
|
|||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 626; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.72.55 (0.011 с.) |

 основная задача интегр. исчисление заданной пр-ой восстановить ф-цию. Пусть ф-ция f(x)определена на интервале(a,b).Опр1:Первообразной ф-цией f(x)на интервале (a,b) н-ся д-мая ф-ция F(x)для которой
основная задача интегр. исчисление заданной пр-ой восстановить ф-цию. Пусть ф-ция f(x)определена на интервале(a,b).Опр1:Первообразной ф-цией f(x)на интервале (a,b) н-ся д-мая ф-ция F(x)для которой  Т1.(основное св-во первообразных) Любые 2 первообразные одной и той же ф-ции отличаются постоянным слогаемым. Опр2.Совокупность всех первообразных ф-ции f(x) на интервале (a,b)н-ся неопр.интегралом от ф-ции f(x)и обозначается
Т1.(основное св-во первообразных) Любые 2 первообразные одной и той же ф-ции отличаются постоянным слогаемым. Опр2.Совокупность всех первообразных ф-ции f(x) на интервале (a,b)н-ся неопр.интегралом от ф-ции f(x)и обозначается  , а F(x)-какая-либо первообразная. Ф-ция f(x) –подынтегральная ф-ция, f(x)dx-подынтегральное выражение. Интегрирование-многозначная операция. Осн.св-ва неопр.интегр:1)
, а F(x)-какая-либо первообразная. Ф-ция f(x) –подынтегральная ф-ция, f(x)dx-подынтегральное выражение. Интегрирование-многозначная операция. Осн.св-ва неопр.интегр:1)  2)
2)  3)
3)  =f(x)+C 4)
=f(x)+C 4)  Св-ва 1-4 показывают, что нтегр и диф яв-ся взаимообратными операциями.5)
Св-ва 1-4 показывают, что нтегр и диф яв-ся взаимообратными операциями.5)  6)
6)  5-6 св-ва линейности неопр интеграла.
5-6 св-ва линейности неопр интеграла. 2)
2) 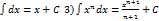 , n
, n 
 4)
4)  5)
5) 
 6)
6)  7)
7)  8)
8)  9)
9)  10)
10) 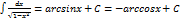 11)
11) 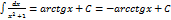 12)
12)  13)
13)  14)
14)  15)
15)  16)
16)  17)
17)  18)
18)  19)
19) 
 , где P(x) и Q(x)- многочлены с действительными коэффициентами. Рациональная дробь называется правильной, если степень многочлена в числителе меньше степени многочлена в знаменателе и неправильной – в противном случае. Если дробь неправильная, то разделив числитель на знаменатель по правилу деления многочленов, можно представить данную дробь в виду суммы многочлена на некоторой правильной дроби. Таким образом, интегрирование неправильной дроби сводится к интегрированию многочлена (что представляет собой простую задачу) и интегрированию правильной дроби. Для нахождения интеграла от правильной рациональной дроби необходимо в начале разложить знаменатель дроби на произведение сомножителей и неприводимых квадратных трехчленов (дискриминант которых меньше нуля)
, где P(x) и Q(x)- многочлены с действительными коэффициентами. Рациональная дробь называется правильной, если степень многочлена в числителе меньше степени многочлена в знаменателе и неправильной – в противном случае. Если дробь неправильная, то разделив числитель на знаменатель по правилу деления многочленов, можно представить данную дробь в виду суммы многочлена на некоторой правильной дроби. Таким образом, интегрирование неправильной дроби сводится к интегрированию многочлена (что представляет собой простую задачу) и интегрированию правильной дроби. Для нахождения интеграла от правильной рациональной дроби необходимо в начале разложить знаменатель дроби на произведение сомножителей и неприводимых квадратных трехчленов (дискриминант которых меньше нуля) и ò
и ò  dx находятся методом подведения под знак дифференциала с использование равенств d(sinx)=cosxdx; d(cosx)=sinxdx, d(tgx)=
dx находятся методом подведения под знак дифференциала с использование равенств d(sinx)=cosxdx; d(cosx)=sinxdx, d(tgx)=  ; d(ctgx)=-
; d(ctgx)=-  Универсальная подстановка Рациональной функцией R(U,V) двух переменных U и V называется функция, представляющая собой частное двух многочленов от этих переменных. Если подынтегральная функция является рациональной относительно U=sinx, V=cosx, то применяется подстановка tg
Универсальная подстановка Рациональной функцией R(U,V) двух переменных U и V называется функция, представляющая собой частное двух многочленов от этих переменных. Если подынтегральная функция является рациональной относительно U=sinx, V=cosx, то применяется подстановка tg  =t. Тогда sinx=
=t. Тогда sinx= 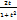 , cosx
, cosx  ,
,  . Таким образом, интеграл от рациональных функций по переменным U=sinx и V=cosx можно свести к интегралу от рациональной функции переменной t. Интегрирование рациональной функции переменной t представляет собой задачу об интегрировании рациональной дроби, которая всегда решается явно. Следовательно, рассмотренная подстановка дает возможность найти в конечном виде (т.е. выразить через элементарные функции) любой интеграл òR(sinx,cosx)dx. Именно поэтому она получила название «универсальной»
. Таким образом, интеграл от рациональных функций по переменным U=sinx и V=cosx можно свести к интегралу от рациональной функции переменной t. Интегрирование рациональной функции переменной t представляет собой задачу об интегрировании рациональной дроби, которая всегда решается явно. Следовательно, рассмотренная подстановка дает возможность найти в конечном виде (т.е. выразить через элементарные функции) любой интеграл òR(sinx,cosx)dx. Именно поэтому она получила название «универсальной»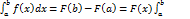 Числа a и b называются нижним и верхним пределом интегрирования. Основные правила и свойства определенного интеграла. Физический смысл определенного интеграла: Пусть S, пройденный телом при прямолинейном движении со скоростью v(t) за интервал времени от
Числа a и b называются нижним и верхним пределом интегрирования. Основные правила и свойства определенного интеграла. Физический смысл определенного интеграла: Пусть S, пройденный телом при прямолинейном движении со скоростью v(t) за интервал времени от  до
до  вычисляется по формуле S=
вычисляется по формуле S=  Геометрический смысл определенного интеграла: Площадь S криволинейной трапеции (фигуры, ограниченной графиком непрерывной положительной на интервале [a;b] функции y=f(x), осью OX и прямыми x=a и x=b) вычисляется по формуле S=
Геометрический смысл определенного интеграла: Площадь S криволинейной трапеции (фигуры, ограниченной графиком непрерывной положительной на интервале [a;b] функции y=f(x), осью OX и прямыми x=a и x=b) вычисляется по формуле S= 



