
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операция над пределами последовательностей.Содержание книги
Поиск на нашем сайте
Правило Лопиталя 33. Локальный и глобальный экстремум функции 34. Выпуклость и вогнутость графика функций. Точки перегиба. 35. Асимптоты графика функций. 36. Алгоритм полного исследования функции для построения её графика. 37. Функции двух переменных, геометрический смысл. Линии уровня поверхности. 38. Предел и непрерывность функции двух переменных. 39.Частные производные. Уравнение касательной плоскости и нормали к поверхности. 40. Определение дифференцируемости ф-ции двух переменных.Полный дифференциал, признак полного дифференциала.Приближенные вычисления с помощью полного дифференциала. 41.Частные производные высших порядков. Теорема о смешанных производных. Дифференциалы высших порядков функции 2х перемен-х. 42.Градиент ф-ции.производная по направлению. 43.Экстрэмумы ф-ции двух переменных. 44.Исследование функции 2х перемен-ых на локальный экстремум. 45.Мнимая единица и комплексные числа. Комплексная плоскость и бесконечно большое комплексное число.\ 46. Алгебраическая, тригонометрическая и показательная формы комп-го числа. 47. Операции над комплесными числами. Логарифм компле-го числа 48.Многочлены.Разложение многочленов на множители.. 49. Выделение целой части неправильной алгебраической дроби. 50.Разложение правильной алгебраической дроби на простейшие. 51.Первообразная функция, неопределенный интеграл как множество первообразных, основные свойства неопределенных интегралов. 52.Таблица простейших интегралов. 53.Основные методы интегрирования: алгебраические и тригонометрические преобразования подынтегральной функции, дифференциальное преобразование подынтегральной функции, замена переменной интегрирования, интегрирование по частям. 54. Интегрирование рациональных дробей. 55. Интегрирование тригонометрических функций. 56.Интегрирование иррациональных функций. 57.Определенный интеграл, основные свойства, геометрический смысл. 58.Определенный интеграл с переменным верхним пределом и его свойства. 59. Формула Ньютона-Лейбница. 60.Замена переменной и интегрирование по частям при вычислении определенного интеграла 61.Геометрические и физические приложения определнного интеграла. 62.Несобственные интергалы и определение их сходимости 63.Дифференцальные уравнения 2 порядка: уравнения с разделяющимися прямыми, в полных дифференцалах,однородные и линейные уравнения. 64. Лин. Однородные ДУ 2-го порядка. ФСР однородного лин. ДУ 2 порядка. Теорема о структуре решения 65. Лин. Неоднородные (ЛНДУ) ДУ 2 порядка. Структура общего решения ЛНДУ. 66. Общее решение однородного лин. Ур-ния 2 порядка с постоянными коэффицентами. 67.Нахождение частного и общего реш-ния неоднородного ур-ния 2 порядка с постоянными коэффициентами и специальной правой частью. 68.Метод вариации произвольных постоянных для опр частного решения неоднородного ДУ второго порядка. 69.Решение нормальной системы ДУ. 70.Числовые ряды.Сходимость ряда.Сумма ряда. 71.Простейшие св-ва рядов.Необходимый признак сходимости. 72.Признаки сх-ти рядов с положительными членами. 73.Знакопеременные ряды,абсолютная и условная сх-ти 74.Признак Лейбница сходимости знакочередующегося ряда. 75.Функциональные ряды.Нахождение области сх-ти функционального ряда. 76.Степенные ряды.теорема Абеля. 77.Радиус и интервал сх-ти степенного ряда. 78.Дифференцирование и интегрирование степенных рядов. 79.Приближенные вичисления с помощью рядов(не будет) 80.Ряды Маклорена и Тейилора.Разложение элементарных ф-ций в степенные ряды.
1.Числовые множества, окрестность токи. Пусть R-мн-во действит.чисел.R(-∞;+∞) Между мн-вом действит.чисел R и точками числовой прямой можно установить взаимно однозначное соответствие. Числовые мн-ва: 1)отрезок Расширенная с-ма действит.чисел: 2.Определение ф-ции, способы задания. Пусть X и Y-числовые мн-ва 3.Свойства ф-ции:честность,нечетность,периодичность. Четная ф-ция должны быть опр. На мн-ве симметричном относительно нуля. График четной ф-ции симметрично относительно оси ординат.Четные: 4.Основные элементарные ф-ции и их графики^
2)показательная:
3)логарифмическая: 4)тригонометрические:
5.Сложная ф-ция.Элементарные ф-ции. Ф-ция y=f( 6.Монотонная,обратная и ограниченная ф-ции. Монотонность ф-ции: Возрастающая –ф-ция,у которой большему значению аргумента из этого промежутки соответствует большее значение ф-ции.Убывающая-ф-ция,у которой большему значению аргумента из этого промежутка соответствует меньшее значение ф-ции. Ф-ция н-ся ограниченной,если существует только положительное число М, что │f(x)│ 7.Неявные ф и параметрически заданные ф-ции. Ф-цию н-ют явной,если оназадана ур-нием x=f(x) разрешенном относит У.Ф-ция н-ся заданной не явно.если она ограниченна ур-ием F(x,y)=0не разрешении относительно У.Неявная: 8.Определение последовательности.Св-вапоследовательностей. Последовательностью называетсячисловая ф-ия натурального аргумента.Виды последовательностей:1) Последовательность {xn} называется ограниченной сверху, если существует конечное число М, 9.Действие над последовательностями. 1) 10.Предел последовательности.Связь между сходимостью и ограниченностью последовательности. Опр. 1 – число а наз-ся пределом {xn} lim (n→∞)xn=a, если для любого E>0 найдётся n→∞. Номер nE, зависящий от E, такой, что |xn-a|<E для всех членов последоват-ти с номерами n>nE.Геометрич. смысл предела {}:|U|<β -β<U<β |xn-a|<E -E<xn-a<E -E+a<xn<E+a a-E<xn<a+E. По Е-окрестности точки а найдётся номер na такой, что все члены {} с номерами n>nExnE+1, xnE+2, xnE+3,… будут находитья в E-окрестности точки а. За пределами Е-окрестности т.а может находиться лишь конечное число членов последоват-ти. Опр.2 - {}на-сясходящейся, если она имеет конечный предел, т.е. lim (n→∞)xn=a, a-конечное число. Св-ва пределов{}: 1.если {}имеет предел, то он единственный. 2.если {}сходится, то она ограничена. 3.если xn=ynсущ-ет такой n≥n0, тогда lim(n→∞)xn=lim(n→∞)yn. 4.Если xn≤ynсущ-ет такой n≥n0, тогдаlim(n→∞xn≤lim(n→∞)yn. 5.(Св-во сжимающей переменной) если xn≤yn≤znи lim(n→∞)xn=lim(n→∞)zn=a, тогда lim(n→∞)yn=a. 11.Бесконечно малые и бесконечно большие последовательности и их свойства. Опр1: Последовательности н-ся бм, если предел Опр2 Свойства бм и бб п-тей:1) если Правило Лопиталя Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность Асимптоты графика функций. Говорят, что прямая x=a является вертикальной асимптотой графика непрерывной функции y=f(x), если хотя бы один из пределов Если функция y=f(x) задана для
и тогда прямая Правило Лопиталя 33. Локальный и глобальный экстремум функции 34. Выпуклость и вогнутость графика функций. Точки перегиба. 35. Асимптоты графика функций. 36. Алгоритм полного исследования функции для построения её графика. 37. Функции двух переменных, геометрический смысл. Линии уровня поверхности. 38. Предел и непрерывность функции двух переменных. 39.Частные производные. Уравнение касательной плоскости и нормали к поверхности. 40. Определение дифференцируемости ф-ции двух переменных.Полный дифференциал, признак полного дифференциала.Приближенные вычисления с помощью полного дифференциала. 41.Частные производные высших порядков. Теорема о смешанных производных. Дифференциалы высших порядков функции 2х перемен-х. 42.Градиент ф-ции.производная по направлению. 43.Экстрэмумы ф-ции двух переменных. 44.Исследование функции 2х перемен-ых на локальный экстремум. 45.Мнимая единица и комплексные числа. Комплексная плоскость и бесконечно большое комплексное число.\ 46. Алгебраическая, тригонометрическая и показательная формы комп-го числа. 47. Операции над комплесными числами. Логарифм компле-го числа 48.Многочлены.Разложение многочленов на множители.. 49. Выделение целой части неправильной алгебраической дроби. 50.Разложение правильной алгебраической дроби на простейшие. 51.Первообразная функция, неопределенный интеграл как множество первообразных, основные свойства неопределенных интегралов. 52.Таблица простейших интегралов. 53.Основные методы интегрирования: алгебраические и тригонометрические преобразования подынтегральной функции, дифференциальное преобразование подынтегральной функции, замена переменной интегрирования, интегрирование по частям. 54. Интегрирование рациональных дробей. 55. Интегрирование тригонометрических функций. 56.Интегрирование иррациональных функций. 57.Определенный интеграл, основные свойства, геометрический смысл. 58.Определенный интеграл с переменным верхним пределом и его свойства. 59. Формула Ньютона-Лейбница. 60.Замена переменной и интегрирование по частям при вычислении определенного интеграла 61.Геометрические и физические приложения определнного интеграла. 62.Несобственные интергалы и определение их сходимости 63.Дифференцальные уравнения 2 порядка: уравнения с разделяющимися прямыми, в полных дифференцалах,однородные и линейные уравнения. 64. Лин. Однородные ДУ 2-го порядка. ФСР однородного лин. ДУ 2 порядка. Теорема о структуре решения 65. Лин. Неоднородные (ЛНДУ) ДУ 2 порядка. Структура общего решения ЛНДУ. 66. Общее решение однородного лин. Ур-ния 2 порядка с постоянными коэффицентами. 67.Нахождение частного и общего реш-ния неоднородного ур-ния 2 порядка с постоянными коэффициентами и специальной правой частью. 68.Метод вариации произвольных постоянных для опр частного решения неоднородного ДУ второго порядка. 69.Решение нормальной системы ДУ. 70.Числовые ряды.Сходимость ряда.Сумма ряда. 71.Простейшие св-ва рядов.Необходимый признак сходимости. 72.Признаки сх-ти рядов с положительными членами. 73.Знакопеременные ряды,абсолютная и условная сх-ти 74.Признак Лейбница сходимости знакочередующегося ряда. 75.Функциональные ряды.Нахождение области сх-ти функционального ряда. 76.Степенные ряды.теорема Абеля. 77.Радиус и интервал сх-ти степенного ряда. 78.Дифференцирование и интегрирование степенных рядов. 79.Приближенные вичисления с помощью рядов(не будет) 80.Ряды Маклорена и Тейилора.Разложение элементарных ф-ций в степенные ряды.
1.Числовые множества, окрестность токи. Пусть R-мн-во действит.чисел.R(-∞;+∞) Между мн-вом действит.чисел R и точками числовой прямой можно установить взаимно однозначное соответствие. Числовые мн-ва: 1)отрезок Расширенная с-ма действит.чисел: 2.Определение ф-ции, способы задания. Пусть X и Y-числовые мн-ва 3.Свойства ф-ции:честность,нечетность,периодичность. Четная ф-ция должны быть опр. На мн-ве симметричном относительно нуля. График четной ф-ции симметрично относительно оси ординат.Четные: 4.Основные элементарные ф-ции и их графики^
2)показательная:
3)логарифмическая: 4)тригонометрические:
5.Сложная ф-ция.Элементарные ф-ции. Ф-ция y=f( 6.Монотонная,обратная и ограниченная ф-ции. Монотонность ф-ции: Возрастающая –ф-ция,у которой большему значению аргумента из этого промежутки соответствует большее значение ф-ции.Убывающая-ф-ция,у которой большему значению аргумента из этого промежутка соответствует меньшее значение ф-ции. Ф-ция н-ся ограниченной,если существует только положительное число М, что │f(x)│ 7.Неявные ф и параметрически заданные ф-ции. Ф-цию н-ют явной,если оназадана ур-нием x=f(x) разрешенном относит У.Ф-ция н-ся заданной не явно.если она ограниченна ур-ием F(x,y)=0не разрешении относительно У.Неявная: 8.Определение последовательности.Св-вапоследовательностей. Последовательностью называетсячисловая ф-ия натурального аргумента.Виды последовательностей:1) Последовательность {xn} называется ограниченной сверху, если существует конечное число М, 9.Действие над последовательностями. 1) 10.Предел последовательности.Связь между сходимостью и ограниченностью последовательности. Опр. 1 – число а наз-ся пределом {xn} lim (n→∞)xn=a, если для любого E>0 найдётся n→∞. Номер nE, зависящий от E, такой, что |xn-a|<E для всех членов последоват-ти с номерами n>nE.Геометрич. смысл предела {}:|U|<β -β<U<β |xn-a|<E -E<xn-a<E -E+a<xn<E+a a-E<xn<a+E. По Е-окрестности точки а найдётся номер na такой, что все члены {} с номерами n>nExnE+1, xnE+2, xnE+3,… будут находитья в E-окрестности точки а. За пределами Е-окрестности т.а может находиться лишь конечное число членов последоват-ти. Опр.2 - {}на-сясходящейся, если она имеет конечный предел, т.е. lim (n→∞)xn=a, a-конечное число. Св-ва пределов{}: 1.если {}имеет предел, то он единственный. 2.если {}сходится, то она ограничена. 3.если xn=ynсущ-ет такой n≥n0, тогда lim(n→∞)xn=lim(n→∞)yn. 4.Если xn≤ynсущ-ет такой n≥n0, тогдаlim(n→∞xn≤lim(n→∞)yn. 5.(Св-во сжимающей переменной) если xn≤yn≤znи lim(n→∞)xn=lim(n→∞)zn=a, тогда lim(n→∞)yn=a. 11.Бесконечно малые и бесконечно большие последовательности и их свойства. Опр1: Последовательности н-ся бм, если предел Опр2 Свойства бм и бб п-тей:1) если Операция над пределами последовательностей. Арифмитические операции над пределами сходящихся последовательностей: Пусть
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.18.59 (0.008 с.) |

 ,2)интервал
,2)интервал  , 3)полуинтервал(полуотрезки)
, 3)полуинтервал(полуотрезки)  Если а и b конечные числа,то числовой промежуток назыв.конечным.Если хотя бы одно из чисел а или b бесконечно,точислов.промежуток назыв.бесконечным(а; +∞)
Если а и b конечные числа,то числовой промежуток назыв.конечным.Если хотя бы одно из чисел а или b бесконечно,точислов.промежуток назыв.бесконечным(а; +∞) . Св-ва
. Св-ва 
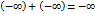 ,2)если а-действительное
,2)если а-действительное  , 3)если
, 3)если 
 ,)4)
,)4)  5)
5)  , 5)
, 5)  . Замечание:след.выражения назыв.неопределёнными:
. Замечание:след.выражения назыв.неопределёнными:  Окрестность точки(U): Пусть
Окрестность точки(U): Пусть  ллюбое число положительное,как правило маленькое (относительно). Опр1:
ллюбое число положительное,как правило маленькое (относительно). Опр1:  -окрестностью точки а н-ся интервал
-окрестностью точки а н-ся интервал 
 . Опр: переменная внличина у н-ся ф-ей независимой переменной х, если к каждому
. Опр: переменная внличина у н-ся ф-ей независимой переменной х, если к каждому  по определению закону или правилу ставится соответсвие вполне опр-ное единичное значение
по определению закону или правилу ставится соответсвие вполне опр-ное единичное значение  .
.  законы соответствия. Область определения D(y)=X. E(y)=Y-мн-во значений. Задать ф-цию-указать ее область опред. и закон соответствия..Опр:Графиком ф-ии y=f(x) опред. На мн-ве X н-ся м-во точек в плоскости
законы соответствия. Область определения D(y)=X. E(y)=Y-мн-во значений. Задать ф-цию-указать ее область опред. и закон соответствия..Опр:Графиком ф-ии y=f(x) опред. На мн-ве X н-ся м-во точек в плоскости  Способы значения ф-ции:1)аналитический-задание ф-ции с помощью формулы.При таком способе задания область орп.ф-ции-ъто совокупность всех действит Х, которым соответствуют действ значения У,2)Табличный-закон соответствия между Х и У опр-ся таблицей,3)графический-закон соответствия сежду х и у опр-ся гарфиком,4) словесный-ф-ция Дирихля.
Способы значения ф-ции:1)аналитический-задание ф-ции с помощью формулы.При таком способе задания область орп.ф-ции-ъто совокупность всех действит Х, которым соответствуют действ значения У,2)Табличный-закон соответствия между Х и У опр-ся таблицей,3)графический-закон соответствия сежду х и у опр-ся гарфиком,4) словесный-ф-ция Дирихля. .Нечетность:симметричен относительно начала координат.Нечетная-ф-ция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x)=-f(x).Периодичность.ф-ция f(x) –периодическая,если существует такое отличное от нуля число Т, что для любого х из области определения ф-ции имеет место:f(x+T)=f(x).Такое наименьшее число н-ся периодом ф-ции.Все тригонометрические ф-ции яв-ся периодичными.
.Нечетность:симметричен относительно начала координат.Нечетная-ф-ция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x)=-f(x).Периодичность.ф-ция f(x) –периодическая,если существует такое отличное от нуля число Т, что для любого х из области определения ф-ции имеет место:f(x+T)=f(x).Такое наименьшее число н-ся периодом ф-ции.Все тригонометрические ф-ции яв-ся периодичными. степеная ф-ция(
степеная ф-ция(










 , определенная на мн-ве Х,н-ся сложной ф-цией от аргумента х.Область значения ф-ции y=
, определенная на мн-ве Х,н-ся сложной ф-цией от аргумента х.Область значения ф-ции y=  (x)яв-ся областью опр ф-ции y=f(U). Ф-цию полученную в результате спер позиций н-ют сложной ф-цией.Элементраная ф-ция задается одной формулой. Элементарной-н-ют ф-цию. Которая задается одной формулой y=f(x), где выражения справа составлео из основных элементов ф-ций и постоянных при помощи конечного числа арифм.операций и конечного числа суперпозиций этих ф-ций.
(x)яв-ся областью опр ф-ции y=f(U). Ф-цию полученную в результате спер позиций н-ют сложной ф-цией.Элементраная ф-ция задается одной формулой. Элементарной-н-ют ф-цию. Которая задается одной формулой y=f(x), где выражения справа составлео из основных элементов ф-ций и постоянных при помощи конечного числа арифм.операций и конечного числа суперпозиций этих ф-ций. M для всех значений Х.если такого числа не сущ-ет,то ф-ция-неограничена..ОПР.Ф-ция определенная на мн-ве Y,ставяща в соответствии каждому у из мн-ва У его прообраз н-ся обратной к ф-ции
M для всех значений Х.если такого числа не сущ-ет,то ф-ция-неограничена..ОПР.Ф-ция определенная на мн-ве Y,ставяща в соответствии каждому у из мн-ва У его прообраз н-ся обратной к ф-ции  и обозначается
и обозначается  При построении обр ф-ции у каждого у из мн-ва У должен быть прообраз
При построении обр ф-ции у каждого у из мн-ва У должен быть прообраз  должен быть единым.Поэтому обратную ф-цию можно построить для монотонно возрастающей, монотонно убывающей ф-ции.
должен быть единым.Поэтому обратную ф-цию можно построить для монотонно возрастающей, монотонно убывающей ф-ции. Явная:
Явная:  .Параметрически заданные ф-ции зависимость между Х и У опр.через параметр.
.Параметрически заданные ф-ции зависимость между Х и У опр.через параметр.  t-параметр
t-параметр .2) Последовательность {xn} называется ограниченной снизу, если существует конечное число N,
.2) Последовательность {xn} называется ограниченной снизу, если существует конечное число N,  .3)
.3)  -ограниченной,если она ограничена сверху и снизу. 4)
-ограниченной,если она ограничена сверху и снизу. 4)  -н-ся монотонно возрастающей(убывающей),если
-н-ся монотонно возрастающей(убывающей),если 
 -сумма двух послед. 2)
-сумма двух послед. 2)  -разность 2-х послед. 3)
-разность 2-х послед. 3)  -произведение 2-х послед. 4)
-произведение 2-х послед. 4)  частное 2-х послед
частное 2-х послед 


 н-ся бб, если
н-ся бб, если 
 - бм, то она ограничена;2) сумма конечного числа бесконечн малых последовательностейесть бесконечно малая последовательность;3)произведение бм
- бм, то она ограничена;2) сумма конечного числа бесконечн малых последовательностейесть бесконечно малая последовательность;3)произведение бм  на ограниченную
на ограниченную  -бб;5)если
-бб;5)если  или
или  . Пусть a является некоторым конечным действительным числом или равно бесконечности. Если
. Пусть a является некоторым конечным действительным числом или равно бесконечности. Если  и
и  , то
, то  ; если
; если  и
и  , то аналогично
, то аналогично  . Первые две неопределенности
. Первые две неопределенности  можно свести к типу
можно свести к типу  или
или  с помощью алгебраических преобразований. А неопределенности
с помощью алгебраических преобразований. А неопределенности  сводятся к типу
сводятся к типу  с помощью соотношения
с помощью соотношения 
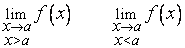 равен ∞.
равен ∞. , то говорят, что прямая y=kx+b является наклонной асимптотой непрерывной кривой y=f(x) при
, то говорят, что прямая y=kx+b является наклонной асимптотой непрерывной кривой y=f(x) при  , если f(x)=kx+b+a(x), где
, если f(x)=kx+b+a(x), где  , т. е.
, т. е.  - бесконечно малая функция при
- бесконечно малая функция при  Т е о р е м а. Для того чтобы график функции y=f(x) имел при
Т е о р е м а. Для того чтобы график функции y=f(x) имел при 
 наклонную асимптому, необходитмо и достаточно, чтобы существовали конечные пределы
наклонную асимптому, необходитмо и достаточно, чтобы существовали конечные пределы ,
, есть асимптота
есть асимптота ,
,  a и b-конечные числа,тогда:1)
a и b-конечные числа,тогда:1)  ; 2)
; 2)  ;3)
;3)  , если b
, если b 



