
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определенный интеграл с переменным верхним пределом и его свойстваСодержание книги
Поиск на нашем сайте
60.Замена переменной и интегрирование по частям при вычислении определенного интеграла. 1. Непосредств. интегриров-е основано на тождественных преобр-х под знаком интеграла, применениисв-в линейности опр-го интеграла, таблице неопр-х интегралов и применении формулы Ньютона-Лейбница. 2. Подстановка или замена переменной в опр-м интеграле: Пусть f(x) неопр. на [a,b], а ф-ияx=ϕ(t) имеет непрерывную производную на[α,β] и при t∈[α,β], x=ϕ(t)∈[a,b], причём ϕ(t)=a, ϕ(β)=b. Тогда: b x=ϕ(t) ∫f(x)dx= dx=ϕ'(t)dt = ∫f(ϕ(t))ϕ'(t)dt. a ϕ(α)=a ϕ(β)= b. При применении этой формулы надо не забыть поменять пределы интегриров-я. 3. Интегриров-е по частям в опр-м интеграле. Теорема. Пусть ф-ииU(x) и V(x) имеют непрерывные производные на [a,b]. Тогда: bbb ∫UdV = U∙V ⎸VdU, гдеU∙V ⎸ = U(b)∙V(b)-U(a)∙V(a). aaa 61.Геометрические и физические приложения определнного интеграла. Геометрическое приложение. І Вычисление площадей плоских фигур. 1)Y=f(x), f(x)≥0 при x∈ [a,b] 62. Несобственные интеграли и опредление их сходимости. ∫ba f(x)dx В определении опр. Интеграла по Риману должны выполняться 2 требования: 1)пределы а и б-конечные числа 2)f(x) должна быть ограничена на [a,b] Если хотя бы одно из двух требований нарушается, то мы имеем дело с несобственными интегралами. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 1 РОДА: ∫+∞а f(x)dx f(x) определена на [a, +∞] и интегрируема на [a, A] при каждом конечном А≥а 63.Дифференцальные уравнения 2 порядка: уравнения с разделяющимися прямыми, в полных дифференцалах,однородные и линейные уравнения. ДУ наз. Ур-ние вида F(x,y,y’,y’’,…,y(n))=0, где x-независимая переменная, y(x)-неизвестная ф-ия, y’,y’’,…,y(n) – производные неизвестной ф-ции. Порядок ДУ определяется по формуле старшей производной, входящей в это ур-ние. Решение ДУ на (a,b) наз. Всякая ф-ия y=фи(x), удовлетворяющая ДУ на (a,b). Решение ДУ наз. Интегральными прямыми. Если у зависит от одной переменной, то ДУ наз. Обыкновенными. Если неизвестная ф-ия хависит от двух и более переменных, то ур-ние содержащая у ф-ию и её частные производные наз. Ур-нием математической физики. ДУ первого порядка наз. Ур-ние вида F(x,y,y’)=0 (1) или y’=f(x,y) (1’),где x-независимая переменная, y(x)-неизвестная ф-ия, y’-производная неизвестной ф-ии. Ур-ние (1’) наз. Ур-нием разрешённым относительно производной. Решением ур-ния (1) наз. Всякая ф-ия удовлетворяющая ур-yb. (1) на (a,b) Общим решением ур-ния (1) наз ф-ия y=фи (x,C) зависящая от переменной х и одной произвольной постоянной С и удовлетворяющая ур-нию (1) при любом значении постоянной С. Частным решение ур-ния (1) наз решение полученное из общего при конкретном значении постоянной С. Начальными условиями для ДУ 1-го порядка наз пара х0, у0, к-рая записываетя в виде y│x-x0=y0 или y(x0)=y0 Решением задачи Коши с нач. условиями х0, у0 наз частное решение y=фи(х, С0), удовлетворяющее заданным нач усл. У0=фи(х0, С0) Теорема Коши (о существовании и единственности решения). ПУСТЬ в ур-нии y’=f(x,y) правая часть f(x,y) и f’y(x,y)непрерывны в обл. Д С R2, тогда любая точка (х0, у0)?Д сущ и притом единственное решение ур-ния у=фи(х,С0) проходящее через точку (х0, у0) Особое решение ДУ(1) это решение ур-ния (1), к-рое нельзя получить из общего решения ни при каком значении С. Замечание: в общем реш-нии ур-ния (1) у явл явной ф-ией, у=фи(х, С), если при интегрировании ур-ния решения в явном виде не удаётся найти, т.е. получается зависимость Ф(х,у,С)=0 то тогда ур-ние у=фи (х, С) наз общим интегралом ур-ния (1) ДУ 1 порядка с разделёнными переменными наз ур-ние вида Р(х)dx+Q(y)dy=0 P(x)dx=-Q(y)dy C+∫P(x)dx=-∫Q(y)dy- общий интеграл исходного ур-ния ДУ 1 порядка с разделяющимися переменными наз. Ур-ние вида M1(x)N1(y)dx+M2(x)N2(y)dy=0 M1(x), N1(y), M2(x), N2(y)-известные непрерывные ф-ии M1(x)N1(y)dx+M2(x)N2(y)dy=0 │: N1(y)M2(x)≠0 M1(x) / M2(x) dx+N2(y)/N1(y) dy=0 Получилось ур-ние с разделёнными переменными Замечание: после реш-ния ур-ния надо проверить не явл ли ф-ии у=у1, х=х1, где N1(y1)=0 M2(x1)=0 решениями исходного ур-ния f(x,y) наз однородной ф-ией n-го измерения по своим переменным, если f(tx,ty)=tn f(x,y) однородной ф-ией нулевого измерения по своим переменным наз f(x,y) удовлетворяющая условию f(tx,ty)=f(x.y) свойства:1) Однородная ф-ия нулевого измерения фактически зависит от отношения y/x f(tx,ty)=f(x/x, y/x)=f(1, y/x)=f(x,y) при t=1/x 2)Отношение двух однородных ф-ий одного и того же измерения есть однородная ф-ия нулевого измерения Однородным диффер-ым ур-нием 1 порядка наз. Ур-ние разрешённое относительно производной y’=f(x,y) правая часть кот-го явл. Однородной ф-ией нулевого измерения. f(tx,ty)=f(x,y) Решением ур-ния ищем в виде y=xu(x), где u(x)-неизвестная ф-ия. y’=u(x)+xu’(x) подставим y=xu и y’=u+xu’ в исходное ур-ние u+xu’=f(x,xu) u+xu’=x0 f(1;u) –т.к. f-однородная ф-ия нулевого измерения u+xu’=f(1,u) (*) ур-ние (*)-это ур-ние с разделяющимися переменными xu’=f(1,u)-u x•du/dx=f(1,u)-u du/f(1,u)=dx/x ∫du/(f(1,u)-u)=∫(dx/x) ∫(du/f(1,u)-u)=ln│x│+C - общий интеграл вспомогателного ур-ния(*) Чтобы получить общий интеграл исходного ур-ния надо в общий интеграл вспомогательного ур-ния (*)заменить u на y/x Линейным ДУ 1 порядка наз. Ур-ние вида: a(x)y’+b(x)y=C(x) или y’+p(x)y=q(x) (1) a(x), b(x), c(x), p(x), q(x)-известные непрерывные ф-ии Ур-ние наз. Линейным потому что y и y’ входят в это ур-ние в первой степени Решение ур-ния ищется в виде: y(x)=u(x)•v(x), где u(x)и v(x)-неизвестные ф-ии y’=u’(x)•v(x)+u(x)•v’(x)=u’•v+u•v’ подставим y и y’ в ур-ние (1) u’•v+u•v’+p(x)u•v=q(x) (*) Замечания: Чтобы решить лин. Ур-ние надо решить 2 ур-ния с разделяющимися перменными Получится общее решение исходного ур-ния 64. Лин. Однородные ДУ 2-го порядка. ФСР однородного лин. ДУ 2 порядка. Теорема о структуре решения ЛОДУ 2 порядка наз ур-ние вида: Y’’+ P(x)y’+Q(x)y=0 (2) P(x) и Q(x) –известные непрерывные ф-ии Ур-ние однородное потому что в правой части стоит 0. Ур-ние линейное, т.к. y, y’, y’’ входят в ур-ние в 1 степени Св-ва решений ур-ния (2): 1)Если y1 и y2-решения ур-ния (2), то y1+y2-решения ур-ния (2) 2)Если y1-решение ур-ния (2), то Су1-решение ур-ния (2), где С-постоянная Из св-в 1 и 2 следует что множество решений ЛОДУ явл. Лин. Пространством. ФСР ЛОДУ(2)наз. Любая пара лин. Незав нешений этого ур-ния Теорема о структуре общего решения ЛОДУ: пусть y1(x) и y2(x) образуют ФСР ур-ния (2) тогда общее решение y(x) ур-ния (2) может быть записано в виде y(x)=C1y1(x)+C2y2(x), где С1 и С2-произвольные постоянные 65. Лин. Неоднородные (ЛНДУ) ДУ 2 порядка. Структура общего решения ЛНДУ. ЛНДУ 2 порядка наз. Ур-ние вида: y’’+P(x)y’+Q(x)y=f(x) (3) Ур-ние лин, т.к. y,y’,y’’ входят в ур-ние 1 степени, ур-ние неоднородное т. К. правая часть f(x)≠0 P(x), Q(x)-известные непрерывные ф-ии. Св-ва решений ур-ния (3): Пусть y1-решение НД (3), а y2-решение ОУ (2), тогда y1+y2-решение НУ (3). Теорема о структуре общего решения ЛНДУ 2 порядка: Пусть y-общее решение лин. Неоднородного ур-ния (3). y͞-общее решение соответствующего ему лин. Ур-ния (2) y*-частное реш-ние ЛНУ (3), тогда y= y͞+ y* 66. Общее решение однородного лин. Ур-ния 2 порядка с постоянными коэффицентами. ЛОДУ 2 порядка с постоянными коэфф. Наз ур-ние вида y’’+py’+qy=0 (7) P,q-постоянные числа Реш-ние ур-ния (7) будем искать в виде y=ekx K2+pk+q=0 (8)-характеристическое ур-ние для ур-ния (7) Y’’→k2 Y’→k y→1 Вид общего реш-ния ур-ния (7) зависит от корней характеристического ур-ния (8) D=p2-4q˃0, k1≠k2 Y1=ek1x y2=ek2x -решение ур-ния (7) Y1/y2=ek1x/ek2x=e(k1-k2)x≠const Y1,y2-образуют ФСР Y=C1y1+C2y2=C1ek1x+C2ek2x 2)D=p2-4q=0 k1=k2 Y1=ek1x Y2=ek1x•x Y1, y2-решение ур-ния (7) Y1/y2=ek1x/ek1x•x=1/x≠const Y=C1y1+C2y2=C1ek1x+C2xek1x= ek1x(C1+C2x) Y=(C1+C2x)ek1x 3)D˂0 k1=альфа+бетаi K2=альфа-бетаi i=√-1 -мнимая единица y=eальфаx(C1cosбетах+С2sinбетах) 67.Нахождение частного и общего реш-ния неоднородного ур-ния 2 порядка с постоянными коэффициентами и специальной правой частью. ЛНДУ 2 порядка: y’’+py’+qy=f(x) (9) P,q-постоянные Y=y͞+y* Если правая часть ур-ния (9) f(x) имеет спец вид, то частное решение ур-ния (9) подбирают по виду f(x) ①f(x)=Pn(x)eax Pn(x)-известный многочлен степени n Pn(x)=a0xn+a1xn-1+…+an-1x+an 1)число а не явлю корнем характерист. Ур-ния (8) y*=P͠n(͠x)eax, где P͠n(x)-неизвестный многочлен степени n (такой же, как степень Pn(x)) c неопр. Коэффиц. 2)число а явл двукратным корнем характерист. Ур-ния (8), тогда Y*=xP͠n(x)eax 3)число а явл двукратным корнем характерист. Ур-ния (8), тогда Y*=xr P͠n(x)eax r-кратность числа а, как корня характерист. Ур-ния (8) r=0,1,2 ②f(x)=eальфа х(Pn(x)cos бетта х+Qm(x)sin бетта х) Qm(x)-известный многочлен степени n. N=max{n,m} Проверяется число альфа+бетта i, где i=√-1 1)Альфа+бетта i не явл. Корнем характерист. Ур-ния (8), тогда Y*=eальфа х(P͠N(x)cos бетта х+Q͠N(x)sin бетта х), где P͠N(x), Q͠N(x)-неизвестные многочлены с неопр. Коэффициентами степени N. 2)Альфа+бетта i явл однократным корнем характеристич. Ур-ния, тогда Y*=х eальфа х(P͠N(x)cos бетта х+Q͠N(x)sin бетта х) Обе написанные формулы можно объединить в одну: Y*=хr eальфа х(P͠N(x)cos бетта х+Q͠N(x)sin бетта х), где r-кратность числа Альфа+бетта i, как корня характерист. Ур-ния (8). r=0,1. 70.Числовые ряды.Сходимость ряда.Сумма ряда. Пусть Un-некоторая числовая последовательность. {Un}={U1, U2, U3, U4,…,Un,…}, Un∈R. Опр.1-числовым рядом наз-ся выражение вида: ∞ ∑Un=U1+U2+U3+U4+…+Un+… (1) n=1 Un-общий член ряда. Рассмотрим последоват-ть частичных сумм ряда: S1=U1 S2=U1+U2 S3=(U1+U2)+U3=S2+U3 S4=U1+U2+U3+U4=S3+U4 Sn=U1+U2+U3+…+Un-1+Un=Sn-1+Un. Sn=Sn-1+Un. Опр.2-если предел Sn-сущ-ет и конечен, то ряд (1) наз-я сходящимся и его сумма S=limSn. n→∞ Опр.3-если limSn-не сущ-ет или бесконечен, то ряд (1) наз-сярасходящимся.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.2.6 (0.007 с.) |

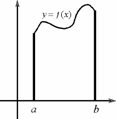 S=∫ba f(x)dx. 2)Y=f(x), f(x)≤0 ∀x∈[a,b]
S=∫ba f(x)dx. 2)Y=f(x), f(x)≤0 ∀x∈[a,b] 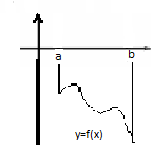 S= -∫ba f(x) dx = │∫ba f(x) dx│ Y=f1(x) Y=f2(x) f1(x)≤ f2(x) ∀x∈[a,b]
S= -∫ba f(x) dx = │∫ba f(x) dx│ Y=f1(x) Y=f2(x) f1(x)≤ f2(x) ∀x∈[a,b] 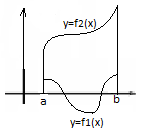 S=∫ba (f2(x) – f1(x)) dx 3)Область ограничена кривой L, заданной параметрически
S=∫ba (f2(x) – f1(x)) dx 3)Область ограничена кривой L, заданной параметрически 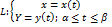 S=∫βα y(t) x’(t) dt = ∫βα x(t) y’(t) dt
S=∫βα y(t) x’(t) dt = ∫βα x(t) y’(t) dt 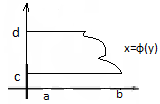 S=∫dc φ(y) dy ІІ Вычисление длины дуги кривой 1)L: y=f(x), при x∈ [a,b]
S=∫dc φ(y) dy ІІ Вычисление длины дуги кривой 1)L: y=f(x), при x∈ [a,b] 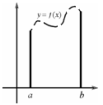 Длина L=∫ba
Длина L=∫ba 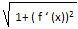 dx 1)
dx 1) 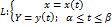 Длина L= ∫βα
Длина L= ∫βα 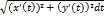 ІІІ Вычисление объёмов тел вращения
ІІІ Вычисление объёмов тел вращения 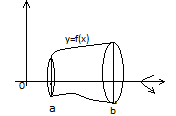 L: y=f(x), ∀x∈[a,b] Vox = П ∫ba f2 (x) dx 1)L: x= φ(y) y∈ [c, d]
L: y=f(x), ∀x∈[a,b] Vox = П ∫ba f2 (x) dx 1)L: x= φ(y) y∈ [c, d] 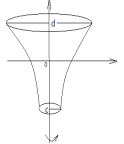 Voy = П ∫dc φ2(y) dy
Voy = П ∫dc φ2(y) dy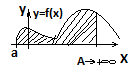 ∫+∞а f(x)dx= lim ∫Aaf(x) dx (1) Если в правой части (1) предел существует и кронечен, то несобственный интеграл в левой части этой формулы наз. Сходящимся. Если в правой части (1) предел бесконечен или не сущ., то несобственный интеграл в левой части этой формулы наз. Расходящимся 2)∫а-∞ f(x) dx f(x) определена на (-∞, a] и интегрируема на каждом отрезке[B, a] при В≤а для любого конечного В.
∫+∞а f(x)dx= lim ∫Aaf(x) dx (1) Если в правой части (1) предел существует и кронечен, то несобственный интеграл в левой части этой формулы наз. Сходящимся. Если в правой части (1) предел бесконечен или не сущ., то несобственный интеграл в левой части этой формулы наз. Расходящимся 2)∫а-∞ f(x) dx f(x) определена на (-∞, a] и интегрируема на каждом отрезке[B, a] при В≤а для любого конечного В. 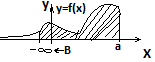 ∫а-∞ f(x) dx=lim ∫aB f(x) dx (2) Рассуждения в (2), такие же как в (1). 3)∫+∞-∞ f(x) dx Пусть f(x) определена на (-∞,+∞) и интегрируема на [a,b] при любых конечных числах a и b. ∫+∞-∞ f(x)dx = ∫a-∞ f(x)dx + ∫+∞af(x)dx (3) Если в правой части (3) оба интеграла сходятся, то интеграл в левой части наз. Сходящимся Если в правой части (3) хотя бы один из двух интегралов расходится, то интеграл в левой части этой части этой формулы наз. Расходящимся. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2 РОДА-это интегралы от неограниченных ф-ий на конечном промежутке 4)∫ba f(x) dx limx→a+0 f(x)=∞ f(x) непрерывна на (a,b]
∫а-∞ f(x) dx=lim ∫aB f(x) dx (2) Рассуждения в (2), такие же как в (1). 3)∫+∞-∞ f(x) dx Пусть f(x) определена на (-∞,+∞) и интегрируема на [a,b] при любых конечных числах a и b. ∫+∞-∞ f(x)dx = ∫a-∞ f(x)dx + ∫+∞af(x)dx (3) Если в правой части (3) оба интеграла сходятся, то интеграл в левой части наз. Сходящимся Если в правой части (3) хотя бы один из двух интегралов расходится, то интеграл в левой части этой части этой формулы наз. Расходящимся. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2 РОДА-это интегралы от неограниченных ф-ий на конечном промежутке 4)∫ba f(x) dx limx→a+0 f(x)=∞ f(x) непрерывна на (a,b] 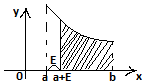 ∫ba f(x) dx=limE→0, E˃0 ∫ba+E f(x) dx (4) рассуждения в (4) такие же как в (1) 5)∫ba f(x)dx limx→b f(x)=∞ f(x) непрерывна на [a,b)
∫ba f(x) dx=limE→0, E˃0 ∫ba+E f(x) dx (4) рассуждения в (4) такие же как в (1) 5)∫ba f(x)dx limx→b f(x)=∞ f(x) непрерывна на [a,b) 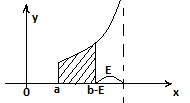 ∫ba f(x)dx=limE→0, E˃0 ∫b-Ea f(x) dx 6)∫ba f(x)dx limx→c f(x)=∞ a˂c˂b f(x) непрерывна на [a,c)Ụ (c,b]
∫ba f(x)dx=limE→0, E˃0 ∫b-Ea f(x) dx 6)∫ba f(x)dx limx→c f(x)=∞ a˂c˂b f(x) непрерывна на [a,c)Ụ (c,b] 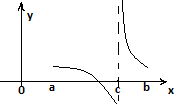 ∫ba f(x)dx = ∫ca f(x)dx + ∫bс f(x)dx(6) Рассуждения в (6), такие же как в (3).
∫ba f(x)dx = ∫ca f(x)dx + ∫bс f(x)dx(6) Рассуждения в (6), такие же как в (3).


