
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность функции одной переменньой в точке .Односторонняя непрерывностьСодержание книги
Поиск на нашем сайте Пусть 19.Свойства в ф-ции.Непрерывность в точке. Поскольку точки 20.Непрерывность сложной, обратной ф-цй. Теорема 1(арифметич.Операции над непрерывными ф-ми). Пусть ф-ииf(x) и g(x) непрерывны в т.x0. Тогда, в т.x0 будут непрерывными: 1.f(x)±g(x) 2.f(x)∙g(x) 3.f(x)/g(x), еслиg(x)≠0. lim(x→x0) f(x)/g(x)=lim(x→x0) f(x)/lim(x→x0) g(x)=f(x0)/g(x0), если g(x0)≠0. Теорема 2.(непрерывность сложной ф-ии). Пусть ф-ияy=f(U) непрерывна в т.U0, а ф-ияU=ϕ(x)непрерывна в т.x0, причём ϕ(x0)=U0. Тогда, сложная ф-ияy=f(ϕ(x)) непрерывна в т.x0 и lim(x→x0) y(x)=lim(x→x0) f(ϕ(x))=f(ϕ(x0)), при этом lim(x→x0) f(ϕ(x))=f(lim(x→x0) ϕ(x))=f(ϕx0)) –возможен предельный переход под знаком непрерывной ф-ии. Теорема 3. Y=f(x) имеет обратную ф-июx=f-1(y) и непрерывна в т.x0∈X. Тогда, обратная ф-ияx=f-1(y) будет непрерывнав т.y0=f(x0). Теорема 4 (о сохр-и знаканепрерывной ф-ии). Пусть ф-ияf(x) непрерывна в т.x0, и f(x0)>0, тогда сущ-ет окрестность в т.x0 (x0-δ, x0+δ), в кот. f(x) тоже будет>0. 21 Непрерывность функции на множестве. Непрерывность элементарных функций. Опр1. 22 Свойства функций, непрерывных на отрезке. Т1:Если ф-ция непрерывна на отрезке
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.006 с.) |

 определенана мн-ве
определенана мн-ве  . F(x)- непрерывная в точке
. F(x)- непрерывная в точке  ,если
,если  ф-ции в точке
ф-ции в точке  опр2.f(x) н-ся непрерывной в точке
опр2.f(x) н-ся непрерывной в точке  (опр.непрерывсности на языке прирощения)
(опр.непрерывсности на языке прирощения) непрерывности функцииf(x) задаются условием
непрерывности функцииf(x) задаются условием  , то часть свойств функций, непрерывных в точке
, то часть свойств функций, непрерывных в точке 
 ,
, 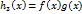 непрерывны в точке
непрерывны в точке  , то функция
, то функция 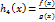 также непрерывна в точке
также непрерывна в точке  . Как непосредственное следствие этой теоремы получается следующее Рассмотрим множество всех функций, определённых в некоторой фиксированной окрестности
. Как непосредственное следствие этой теоремы получается следующее Рассмотрим множество всех функций, определённых в некоторой фиксированной окрестности  точки
точки  является линейным пространством, то есть замкнуто относительно сложения и умножения на постоянные:
является линейным пространством, то есть замкнуто относительно сложения и умножения на постоянные:  Доказательство. Действительно, постоянные
Доказательство. Действительно, постоянные  это непpеpывные функции (в любой точке); по пpедыдущей теоpеме тогда непpеpывны в точке
это непpеpывные функции (в любой точке); по пpедыдущей теоpеме тогда непpеpывны в точке  . Но тогда по этой же теоpеме непpеpывна в точке
. Но тогда по этой же теоpеме непpеpывна в точке  . Т 2 Пусть функции f и g таковы, что существует композиция
. Т 2 Пусть функции f и g таковы, что существует композиция  ,
,  . Пусть функция g непрерывна в точке
. Пусть функция g непрерывна в точке  , а функция f непрерывна в соответствующей точке
, а функция f непрерывна в соответствующей точке 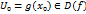 . Тогда композиция h=f*g непрерывна в точке
. Тогда композиция h=f*g непрерывна в точке  означает, что при
означает, что при  будет
будет  . Значит,
. Значит,  (последнее равенство следует из непрерывности функции f в точке
(последнее равенство следует из непрерывности функции f в точке  ). Значит,
). Значит,  , а это равенство означает, что композиция
, а это равенство означает, что композиция  непрерывна в точке
непрерывна в точке  или
или  и получить аналогичные утверждения для непрерывности слева или справа: Т 3 Пусть функцииf(x) и g(x) непрерывны слева (справа) в точке
и получить аналогичные утверждения для непрерывности слева или справа: Т 3 Пусть функцииf(x) и g(x) непрерывны слева (справа) в точке 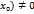 , то функция
, то функция  . Тогда композицияh=f*g непрерывна слева (соотв. справа) в точке
. Тогда композицияh=f*g непрерывна слева (соотв. справа) в точке  н-ся непрерывной на мн-ве Х, если она не прерывна в каждой точке этого мн-ва. Непрерывность нек ф-ций:
н-ся непрерывной на мн-ве Х, если она не прерывна в каждой точке этого мн-ва. Непрерывность нек ф-ций:  2)y=x, при
2)y=x, при  (у=х непрерывна на всей числовой оси)3)
(у=х непрерывна на всей числовой оси)3)  Эта ф-ция непрерывна на всей числовой оси, как произведение непрерывных мн-телей.4)Целая рациональная ф-ция
Эта ф-ция непрерывна на всей числовой оси, как произведение непрерывных мн-телей.4)Целая рациональная ф-ция  Непрерывная ф-ция на всей числовой оси, как сумма непрерывных слагаемых(каждое слагаемое есть произведение непрерывных ф-ций постоянной, степенной)5)Дробно-рациональная ф-ция
Непрерывная ф-ция на всей числовой оси, как сумма непрерывных слагаемых(каждое слагаемое есть произведение непрерывных ф-ций постоянной, степенной)5)Дробно-рациональная ф-ция  отношение 2-х многочленов непрерывно в тех точках, где знаменатель
отношение 2-х многочленов непрерывно в тех точках, где знаменатель  .6)y=sinx(тригонометрическая) Из опр непрерывности ф-ции на языке прирощений следует, что y=sinx-непрерывна в люб точке числовой оси. 7) y=cosx-непрерывна, как сложная ф-ция от двух непрерывных ф-ций.8)y=tgx, y=ctgx- непрерывны в своей области определения.9) обратные тригонометрические ф-ции непрерывны-по теореме о непрерывности обратной ф-ции. Т1:Всякая элементарная ф-ция непрерывна в своей области определения.
.6)y=sinx(тригонометрическая) Из опр непрерывности ф-ции на языке прирощений следует, что y=sinx-непрерывна в люб точке числовой оси. 7) y=cosx-непрерывна, как сложная ф-ция от двух непрерывных ф-ций.8)y=tgx, y=ctgx- непрерывны в своей области определения.9) обратные тригонометрические ф-ции непрерывны-по теореме о непрерывности обратной ф-ции. Т1:Всякая элементарная ф-ция непрерывна в своей области определения. ,то на этом отрезке она ограничена. Т2: Если f(x) непрерывна на отрезке
,то на этом отрезке она ограничена. Т2: Если f(x) непрерывна на отрезке  , тогда для
, тогда для  ,в которой
,в которой 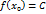 . Т4: Пусть ф-ция y=f(x) непрерывна на отрезке
. Т4: Пусть ф-ция y=f(x) непрерывна на отрезке  , в которой
, в которой 



