
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Простейшие св-ва рядов.Необходимый признак сходимости.Содержание книги
Поиск на нашем сайте
Основные св-ва 1.Если все члены ряды умножить на одно и тоже число не равное 0,то это действие не влияет на сходимость ряда 2.Если к ряду вы прибавите конечное число слагаемых или удалить из него конечгое число членов ряда, сх-сть ряда не изменится. Теорема (необход.признак сх-ти ряда) Если ряд сх-тся то общий член ряда стремится к 0 Замечание. Обратное утверждение к теор.вообще говоря не верно:из того что общий член ряда стремится к 0 Примеры Un=1/n 2) Признаки сх-ти рядов с положительными членами. Закономерным положительным рядом наз-ся числовой ряд Теорема (критерий сходимости положительного ряда) Для того чтобы ряд с положитедьными членами сх-ся н. и д. чтобы послед-сть частичных сумм этого ряда была ограничена сверху конечными числами. Признаки сравнения 1) 2) Теорема(признак сх-ти положительных рядов) Пусть общие ряды 2 и 3 связаны неравенством Если ряд 3 с большими членами сх-ся то ряд 2 с меньшими чл.расх-ся. Если ряд 2 с меньшими чл. Расходится,то расходится ряд 3 с больш.чл. Тер.(предельный признак сх-ти рядов) Пусть для чл. положит.рядов 2 и 3 В качестве рядов сравнения выбираем один из двух эталонов рядов 1) Расх-ся при q 2)
ряд расх-ся при Признаки сравнения удобно применять к рядам вида Предельный признак удобно применять к рядам,общие члены к-ых яв-ся многочл-ми по n. Теорема(Признак Даламбера) Пусть для полож.ряда 2 Если Замечание 1.при Д=1 вопрос о сх-ти ряда остается открытым 2.если общ.чл. ряда представляет собой отношение многоч-ов по n,то для таких рядов Д=1,таким признак Даламбера не применяется 3.признак Даламбера применяется к рядам общ.чл. к-ых содержат
-показательную функции. -факториалы -накативиющиеся множители Теорема (радикальный признак Коши) Пусть для членов положит.ряда 2 К= Если К Замечание 1.При К=1 вопрос о сх-ти ряда остается открытым 2. 3.Радикальный признак Коши применим к рядам общ.чл.к-ых содержат -показ.ф-ции,степенно показ.ф-цию по n Теорема (Интегральный признак Коши-Маклорена) Пусть ф-ция f(x) удовлетворяет условиям 1)f(x) оредел.и непрерыв.на [1, 2)f(x) 3)f(x) 4)f(x)= Если не собст.интеграл сходится то сх-ся ряд 2.если несобств.интеграл расх-ся то расх-ся ряд2 Знакопеременные ряды,абсолютная и условная сх-ти Ряд Составим ряд из модулей членов ряда (3) Ряд 4 положительный и к нему можно применить достаточные признаки сх-сти полож.рядов. Теорема Если ряд из модулей 4 сх-ся то сх-ся ряд 3. Опр.1знакоперемен. ряд 3 наз-ся абсолютн сходящимся если сх-ся 4 составлен. из модулей его членов. Из теоремы следует что абсолютная сх-сть ряда влечет за собой обычную сх-сть ряда. Опр.2 закономерн.ряд 3наз-ся условно-сходящимся если он сам сх-ся а ряд составленный из модулей его членов расх-ся. Признак Лейбница сходимости знакочередующегося ряда. Знакочередующ.рядом наз-ся ряд любые два соседних членов к-го имеют противоположные знаки.
Теорема.(Признак Лейбница сходимости знакочередующегося ряда.) Если в знакочеред.ряде 5 члены ряда монотонно убывают по абсолют.величине и член ряда Функциональные ряды.Нахождение области сх-ти функционального ряда. Функциональным рядом наз-ся выражение вида:
T-обл.опр.ряда
Если ряд 2 сх-ся то х0 наз-ся т-ой сходимости функционального ряда1. Если ряд 2 расх-ся то х0 наз-ся т-ой расходимости функ-ного ряда1. Областью сх-ти ряда 1 наз-ся совокупность всех точек сх-ти этого ряда. Областью абсолютной сх-ти функ-ного ряда наз-ся совокупность точек в кот.ряд1 сх-ся абсолютно.
При каждом конкретном х ряд 3 положительный При тех х для к-ых Д(х) При тех х к-ых Д(х) При тех х для к-ых Д(х)=1 проводится допол.исследование.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.5.179 (0.009 с.) |

 =1+
=1+  +
+  +
+  +…+
+…+  +… гармонический ряд расх-ся
+… гармонический ряд расх-ся 0 при n
0 при n  =1+
=1+  +
+  ряд сх-ся Un=
ряд сх-ся Un= 
 ,где
,где 

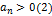
 ,
, 

 =L(
=L( ,тогда оба ряда ведут себя одинаково,т.е.оба сх-ся или расх-ся одинаково.
,тогда оба ряда ведут себя одинаково,т.е.оба сх-ся или расх-ся одинаково. сх-ся при 0
сх-ся при 0 





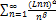 ,
,  ,
, 

 то ряд 2 сх-ся,если Д
то ряд 2 сх-ся,если Д  то ряд 2 расх-ся
то ряд 2 расх-ся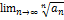
 то ряд 2 сх-ся,К
то ряд 2 сх-ся,К  расх-ся
расх-ся




 (3) наз-ся знакопеременным если он содержит положит и отриц члены.
(3) наз-ся знакопеременным если он содержит положит и отриц члены. (4)
(4)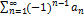 ,где
,где  (5)
(5)
 ,тогда ряд 5 сх-ся и его сумма не превосходит первого члена ряда.
,тогда ряд 5 сх-ся и его сумма не превосходит первого члена ряда. (1)
(1) - общий член ряда
- общий член ряда (2)-числовой ряд
(2)-числовой ряд (3)
(3) 1 ряд 3 получается сходящимся значит ряд 1 сх-ся абсолютно.
1 ряд 3 получается сходящимся значит ряд 1 сх-ся абсолютно. ряды 3 и 1 расх-ся.
ряды 3 и 1 расх-ся.


