
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функциональная методика потоков данныхСодержание книги
Поиск на нашем сайте
Целью методики является построение модели рассматриваемой системы в виде диаграммы потоков данных (Data Flow Diagram — DFD), обеспечивающей правильное описание выходов (отклика системы в виде данных) при заданном воздействии на вход системы (подаче сигналов через внешние интерфейсы). Диаграммы потоков данных являются основным средством моделирования функциональных требований к проектируемой системе. При создании диаграммы потоков данных используются четыре основных понятия: потоки данных, процессы (работы) преобразования входных потоков данных в выходные, внешние сущности, накопители данных (хранилища). Потоки данных являются абстракциями, использующимися для моделирования передачи информации (или физических компонент) из одной части системы в другую. Потоки на диаграммах изображаются именованными стрелками, ориентация которых указывает направление движения информации. Назначение процесса (работы) состоит в продуцировании выходных потоков из входных в соответствии с действием, задаваемым именем процесса. Имя процесса должно содержать глагол в неопределенной форме с последующим дополнением (например, "получить документы по отгрузке продукции"). Каждый процесс имеет уникальный номер для ссылок на него внутри диаграммы, который может использоваться совместно с номером диаграммы для получения уникального индекса процесса во всей модели. Хранилище (накопитель) данных позволяет на указанных участках определять данные, которые будут сохраняться в памяти между процессами. Фактически хранилище представляет "срезы" потоков данных во времени. Информация, которую оно содержит, может использоваться в любое время после ее получения, при этом данные могут выбираться в любом порядке. Имя хранилища должно определять его содержимое и быть существительным. Внешняя сущность представляет собой материальный объект вне контекста системы, являющейся источником или приемником системных данных. Ее имя должно содержать существительное, например, "склад товаров". Предполагается, что объекты, представленные как внешние сущности, не должны участвовать ни в какой обработке. Кроме основных элементов, в состав DFD входят словари данных и миниспецификации. Словари данных являются каталогами всех элементов данных, присутствующих в DFD, включая групповые и индивидуальные потоки данных, хранилища и процессы, а также все их атрибуты. Миниспецификации обработки — описывают DFD -процессы нижнего уровня. Фактически миниспецификации представляют собой алгоритмы описания задач, выполняемых процессами: множество всех миниспецификаций является полной спецификацией системы. Процесс построения DFD начинается с создания так называемой основной диаграммы типа "звезда", на которой представлен моделируемый процесс и все внешние сущности, с которыми он взаимодействует. В случае сложного основного процесса он сразу представляется в виде декомпозиции на ряд взаимодействующих процессов. Критериями сложности в данном случае являются: наличие большого числа внешних сущностей, многофункциональность системы, ее распределенный характер. Внешние сущности выделяются по отношению к основному процессу. Для их определения необходимо выделить поставщиков и потребителей основного процесса, т.е. все объекты, которые взаимодействуют с основным процессом. На этом этапе описание взаимодействия заключается в выборе глагола, дающего представление о том, как внешняя сущность использует основной процесс или используется им. Например, основной процесс – "учет обращений граждан", внешняя сущность – "граждане", описание взаимодействия – "подает заявления и получает ответы". Этот этап является принципиально важным, поскольку именно он определяет границы моделируемой системы. Для всех внешних сущностей строится таблица событий, описывающая их взаимодействие с основным потоком. Таблица событий включает в себя наименование внешней сущности, событие, его тип (типичный для системы или исключительный, реализующийся при определенных условиях) и реакцию системы. На следующем шаге происходит декомпозиция основного процесса на набор взаимосвязанных процессов, обменивающихся потоками данных. Сами потоки не конкретизируются, определяется лишь характер взаимодействия. Декомпозиция завершается, когда процесс становится простым, т.е.: 1. процесс имеет два-три входных и выходных потока; 2. процесс может быть описан в виде преобразования входных данных в выходные; 3. процесс может быть описан в виде последовательного алгоритма. Для простых процессов строится миниспецификация – формальное описание алгоритма преобразования входных данных в выходные. Миниспецификация удовлетворяет следующим требованиям: для каждого процесса строится одна спецификация; спецификация однозначно определяет входные и выходные потоки для данного процесса; спецификация не определяет способ преобразования входных потоков в выходные; спецификация ссылается на имеющиеся элементы, не вводя новые; спецификация по возможности использует стандартные подходы и операции. После декомпозиции основного процесса для каждого подпроцесса строится аналогичная таблица внутренних событий. Следующим шагом после определения полной таблицы событий выделяются потоки данных, которыми обмениваются процессы и внешние сущности. Простейший способ их выделения заключается в анализе таблиц событий. События преобразуются в потоки данных от инициатора события к запрашиваемому процессу, а реакции – в обратный поток событий. После построения входных и выходных потоков аналогичным образом строятся внутренние потоки. Для их выделения для каждого из внутренних процессов выделяются поставщики и потребители информации. Если поставщик или потребитель информации представляет процесс сохранения или запроса информации, то вводится хранилище данных, для которого данный процесс является интерфейсом. После построения потоков данных диаграмма должна быть проверена на полноту и непротиворечивость. Полнота диаграммы обеспечивается, если в системе нет "повисших" процессов, не используемых в процессе преобразования входных потоков в выходные. Непротиворечивость системы обеспечивается выполнением наборов формальных правил о возможных типах процессов: на диаграмме не может быть потока, связывающего две внешние сущности – это взаимодействие удаляется из рассмотрения; ни одна сущность не может непосредственно получать или отдавать информацию в хранилище данных – хранилище данных является пассивным элементом, управляемым с помощью интерфейсного процесса; два хранилища данных не могут непосредственно обмениваться информацией – эти хранилища должны быть объединены. К преимуществам методики DFD относятся: · возможность однозначно определить внешние сущности, анализируя потоки информации внутри и вне системы; · возможность проектирования сверху вниз, что облегчает построение модели "как должно быть"; · наличие спецификаций процессов нижнего уровня, что позволяет преодолеть логическую незавершенность функциональной модели и построить полную функциональную спецификацию разрабатываемой системы. К недостаткам модели отнесем: необходимость искусственного ввода управляющих процессов, поскольку управляющие воздействия (потоки) и управляющие процессы с точки зрения DFD ничем не отличаются от обычных; отсутствие понятия времени, т.е. отсутствие анализа временных промежутков при преобразовании данных (все ограничения по времени должны быть введены в спецификациях процессов). Ответ №14 Вопрос Математическое моделирование. основные принципы построения модели 1. Принцип информационной достаточности. При полном отсутствии информации об исследуемой системе построение ее модели невозможно. При наличии полной информации о системе ее моделирование лишено смысла. Существует некоторый критический уровень априорных сведений о системе (уровень информационной достаточности), при достижении которого может быть построена ее адекватная модель. 2. Принцип осуществимости. Создаваемая модель должна обеспечивать достижение поставленной цели исследования с вероятностью, существенно отличающейся от нуля, и за конечное время. 3. Принцип множественности моделей. Данный принцип является ключевым. Речь идет о том, что создаваемая модель должна отражать в первую очередь те свойства реальной системы (или явления), которые влияют на выбранный показатель эффективности. Соответственно при использовании любой конкретной модели познаются лишь некоторые стороны реальности. Для более полного ее исследования необходим ряд моделей, позволяющих с разных сторон и с разной степенью детальности отражать рассматриваемый процесс. 4. Принцип агрегирования. В большинстве случаев сложную систему можно представить состоящей из агрегатов (подсистем), для адекватного математического описания которых оказываются пригодными некоторые стандартные математические схемы. Принцип агрегирования позволяет, кроме того, достаточно гибко перестраивать модель в зависимости от задач исследования. 5. Принцип параметризации. В ряде случаев моделируемая система имеет в своем составе некоторые относительно изолированные подсистемы, характеризующиеся определенным параметром, в том числе векторным. Такие подсистемы можно заменять в модели соответствующими числовыми величинами, а не описывать процесс их функционирования. При необходимости зависимость значений этих величин от ситуации может задаваться в виде таблицы, графика или аналитического выражения (формулы). Принцип параметризации позволяет сократить объем и продолжительность моделирования. Однако надо иметь в виду, что параметризация снижает адекватность модели. Степень реализации перечисленных принципов и каждой конкретной модели может быть различной, причем это зависит не только от желания разработчика, но и от соблюдения им технологии моделирования. А любая технология предполагает наличие определенной последовательности действий Общая цель моделирования может быть сформулирована следующим образом: это определение (расчет) значений выбранного показателя эффективности (ПЭ) для различных стратегий проведения операции (или вариантов реализации проектируемой системы). При разработке конкретной модели цель моделирования должна уточняться с учетом используемого критерия эффективности. Для критерия пригодности модель, как правило, должна обеспечивать расчет значений ПЭ для всего множества допустимых стратегий. При использовании критерия оптимальности модель должна позволять непосредственно определять параметры исследуемого объекта, дающие экстремальное значение ПЭ [10]. Таким образом, цель моделирования определяется как целью исследуемой операции, так и планируемым способом использования результатов исследования. Например, проблемная ситуация, требующая принятия решения, формулируется следующим образом: найти вариант построения вычислительной сети, который обладал бы минимальной стоимостью при соблюдении требований по производительности и по надежности. В этом случае целью моделирования является отыскание параметров сети, обеспечивающих минимальное значение ПЭ, в роли которого выступает стоимость. Задача может быть сформулирована иначе: из нескольких вариантов конфигурации вычислительной сети выбрать наиболее надежный. Здесь в качестве ПЭ выбирается один из показателей надежности (средняя наработка на отказ, вероятность безотказной работы и т. п.), а целью моделирования является сравнительная оценка вариантов сети по этому показателю. Приведенные примеры говорят о том, что сам по себе выбор показателя эффективности еще не определяет «архитектуру» будущей модели, поскольку на этом этапе не определена концептуальная модель исследуемой системы. В целом при решении любой задачи построения модели основную роль играют следующие четыре элемента [40]: 1) эксперимент; 2) модель; 3) показатели эффективности; 4) критерии принятия решений. Необходимо должным образом определить перечисленные элементы и понять их взаимосвязь, поскольку они оказывают большое влияние на проектирование системы и на планирование ее работы в целом. Критерии принятия решений позволяют выбрать наиболее эффективные параметры системы. Обычно этот процесс называется оптимизацией Принципы и подходы к построению математических моделей. Математическое моделирование многие считают скорее искусством, чем стройной и законченной теорией. Здесь очень велика роль опыта, интуиции и других интеллектуальных качеств человека. Поэтому невозможно написать достаточно формализованную инструкцию, определяющую, как должна строиться модель той или иной системы. Тем не менее отсутствие точных правил не мешает опытным специалистам строить удачные модели. К настоящему времени уже накоплен значительный опыт, дающий основание сформулировать некоторые принципы и подходы к построению моделей. При рассмотрении порознь каждый из них может показаться довольно очевидным. Но совокупность взятых вместе принципов и подходов далеко не тривиальна. Многие ошибки и неудачи в практике моделирования являются прямым следствием нарушения этой методологии. Принципы определяют те общие требования, которым должна удовлетворять правильно построенная модель. Рассмотрим эти принципы. 1. Адекватность. Этот принцип предусматривает соответствие модели целям исследования по уровню сложности и организации, а также соответствие реальной системе относительно выбранного множества свойств. До тех пор, пока не решен вопрос, правильно ли отображает модель исследуемую систему, ценность модели незначительна. 2. Соответствие модели решаемой задаче. Модель должна строиться для решения определенного класса задач или конкретной задачи исследования системы. Попытки создания универсальной модели, нацеленной на решение большого числа разнообразных задач, приводят к такому усложнению, что она оказывается практически непригодной. Опыт показывает, что при решении каждой конкретной задачи нужно иметь свою модель, отражающую те аспекты системы, которые являются наиболее важными в данной задаче. Этот принцип связан с принципом адекватности. 3. Упрощение при сохранении существенных свойств системы. Модель должна быть в некоторых отношениях проще прототипа—в этом смысл моделирования. Чем сложнее рассматриваемая система, тем по возможности более упрощенным должно быть ее описание, умышленно утрирующее типичные и игнорирующее менее существенные свойства. Этот принцип может быть назван принципом абстрагирования от второстепенных деталей. 4. Соответствие между требуемой точностью результатов моделирования и сложностью модели. Модели по своей природе всегда носят приближенный характер. Возникает вопрос, каким должно быть это приближение. С одной стороны, чтобы отразить все скольконибудь существенные свойства, модель необходимо детализировать. С другой стороны, строить модель, приближающуюся по сложности к реальной системе, очевидно, не имеет смысла. Она не должна быть настолько сложной, чтобы нахождение решения оказалось слишком затруднительным. Компромисс между этими двумя требованиями достигается нередко путем проб и ошибок. Практическими рекомендациями по уменьшению сложности моделей являются: • изменение числа переменных, достигаемое либо исключением несущественных переменных, либо их объединением. Процесс преобразования модели в модель с меньшим числом переменных и ограничений называют агрегированием. Например, все типы ЭВМ в модели гетерогенных сетей можно объединить в четыре типа - ПЭВМ, рабочие станции, большие ЭВМ, кластерные ЭВМ; • изменение природы переменных параметров. Переменные параметры рассматриваются в качестве постоянных, дискретные — в качестве непрерывных и т.д. Так, условия распространения радиоволн в модели радиоканала для простоты можно принять постоянными; • изменение функциональной зависимости между переменными. Нелинейная зависимость заменяется обычно линейной, дискретная функция распределения вероятностей - непрерывной; • изменение ограничений (добавление, исключение или модификация). При снятии ограничений получается оптимистичное решение, при введении — пессимистичное. Варьируя ограничениями, можно найти возможные граничные значения эффективности. Такой прием часто используется для нахождения предварительных оценок эффективности решений на этапе постановки задач; • ограничение точности модели. Точность результатов модели не может быть выше точности исходных данных. 5. Баланс погрешностей различных видов. В соответствии с принципом баланса необходимо добиваться, например, баланса систематической погрешности моделирования за счет отклонения модели от оригинала и погрешности исходных данных, точности отдельных элементов модели, систематической погрешности моделирования и случайной погрешности при интерпретации и осреднении результатов. 6. Многовариантность реализаций элементов модели. Разнообразие реализаций одного и того же элемента, отличающихся по точности (а следовательно, и по сложности), обеспечивает регулирование соотношения «точность/сложность». 7. Блочное строение. При соблюдении принципа блочного строения облегчается разработка сложных моделей и появляется возможность использования накопленного опыта и готовых блоков с минимальными связями между ними. Выделение блоков производится с учетом разделения модели по этапам и режимам функционирования системы. К примеру, при построении модели для системы радиоразведки можно выделить модель работы излучателей, модель обнаружения излучателей, модель пеленгования и т.д. В зависимости от конкретной ситуации возможны следующие подходы к построению моделей; • непосредственный анализ функционирования системы; • проведение ограниченного эксперимента на самой системе; • использование аналога; • анализ исходных данных. Имеется целый ряд систем, которые допускают проведение непосредственных исследований по выявлению существенных параметров и отношений между ними. Затем либо применяются известные математические модели, либо они модифицируются, либо предлагается новая модель. Таким образом, например, можно вести разработку модели для направления связи в условиях мирного времени. При проведении эксперимента выявляются значительная часть существенных параметров и их влияние на эффективность системы. Такую цель преследуют, например, все командно-штабные игры и большинство учений. Если метод построения модели системы не ясен, но ее структура очевидна, то можно воспользоваться сходством с более простой системой, модель для которой существует. К построению модели можно приступить на основе анализа исходных данных, которые уже известны или могут быть получены. Анализ позволяет сформулировать гипотезу о структуре системы, которая затем апробируется. Так появляются первые модели нового образца иностранной техники при наличии предварительных данных об их технических параметрах. Разработчики моделей находятся под действием двух взаимно противоречивых тенденций: стремления к полноте описания и стремления к получению требуемых результатов возможно более простыми средствами. Достижение компромисса ведется обычно по пути построения серии моделей, начинающихся с предельно простых и восходящих до высокой сложности (существует известное правило: начинай с простых моделей, а далее усложняй). Простые модели помогают глубже понять исследуемую проблему. Усложненные модели используются для анализа влияния различных факторов на результаты моделирования. Такой анализ позволяет исключать некоторые факторы из рассмотрения. Сложные системы требуют разработки целой иерархии моделей, различающихся уровнем отображаемых операций. Выделяют такие уровни, как вся система, подсистемы, управляющие объекты и др.
Этапы построения математической модели. Сущность построения математической модели состоит в том, что реальная система упрощается, схематизируется и описывается с помощью того или иного математического аппарата. Можно выделить следующие основные этапы построения моделей. 1. Содержательное описание моделируемого объекта. Объекты моделирования описываются с позиций системного подхода. Исходя из цели исследования устанавливаются совокупность элементов, взаимосвязи между элементами, возможные состояния каждого элемента, существенные характеристики состояний и соотношения между ними. Например, фиксируется, что если значение одного параметра возрастает, то значение другого - убывает и т.п. Вопросы, связанные с полнотой и единственностью набора характеристик, не рассматриваются. Естественно, в таком словесном описании возможны логические противоречия, неопределенности. Это исходная естественно-научная концепция исследуемого объекта. Такое предварительное, приближенное представление системы называют концептуальной моделью. Для того чтобы содержательное описание служило хорошей основой для последующей формализации, требуется обстоятельно изучить моделируемый объект. Нередко естественное стремление ускорить разработку модели уводит исследователя от данного этапа непосредственно к решению формальных вопросов. В результате построенная без достаточного содержательного базиса модель оказывается непригодной к использованию. На этом этапе моделирования широко применяются качественные методы описания систем, знаковые и языковые модели. 2. Формализация операций. Формализация сводится в общих, чертах к следующему. На основе содержательного описания определяется исходное множество характеристик системы. Для выделения существенных характеристик необходим хотя бы приближенный анализ каждой из них. При проведении анализа опираются на постановку задачи и понимание природы исследуемой системы. После исключения несущественных характеристик выделяют управляемые и неуправляемые параметры и производят, символизацию. Затем определяется система ограничений на значения управляемых параметров. Если ограничения не носят принципиальный характер, то ими пренебрегают. Дальнейшие действия связаны с формированием целевой функции модели. В соответствии с известными положениями выбираются показатели исхода операции и определяется примерный вид функции полезности на исходах. Если функция полезности близка к пороговой (или монотонной), то оценка эффективности решений возможна непосредственно по показателям исхода операции. В этом случае необходимо выбрать способ свертки показателей (способ перехода от множества показателей к одному обобщенному показателю) и произвести саму свертку. По свертке показателей формируются критерий эффективности и целевая функция. Если при качественном анализе вида функции полезности окажется, что ее нельзя считать пороговой (монотонной), прямая оценка эффективности решений через показатели исхода операции неправомочна. Необходимо определять функцию полезности и уже на ее основе вести формирование критерия эффективности и целевой функции. В целом замена содержательного описания формальным - это итеративный процесс. 3. Проверка адекватности модели. Требование адекватности находится в противоречии с требованием простоты, и это нужно учитывать при проверке модели на адекватность. Исходный вариант модели предварительно проверяется по следующим основным аспектам: • Все ли существенные параметры включены в модель? • Нет ли в модели несущественных параметров? • Правильно ли отражены функциональные связи между параметрами? • Правильно ли определены ограничения на значения параметров? Для проверки рекомендуется привлекать специалистов, которые не принимали участия в разработке модели. Они могут более объективно рассмотреть модель и заметить ее слабые стороны, чем ее разработчики. Такая предварительная проверка модели позволяет выявить грубые ошибки. После этого приступают к реализации модели и проведению исследований. Полученные результаты моделирования подвергаются анализу на соответствие известным свойствам исследуемого объекта. Для установления соответствия создаваемой модели оригиналу используются следующие пути: • сравнение результатов моделирования с отдельными экспериментальными результатами, полученными при одинаковых условиях; • использование других близких моделей; • сопоставление структуры и функционирования модели с прототипом. Главным путем проверки адекватности модели исследуемому объекту выступает практика. Однако она требует накопления статистики, которая далеко не всегда бывает достаточной для получения надежных данных. Для многих моделей первые два пути приемлемы в меньшей степени. В этом случае остается один путь: заключение о подобии модели и прототипа делать на основе сопоставления их структур и реализуемых функций. Такие заключения не носят формального характера, поскольку основываются на опыте и интуиции исследователя. По результатам проверки модели на адекватность принимается решение о возможности ее практического использования или о проведении корректировки. 4. Корректировка модели. При корректировке модели могут уточняться существенные параметры, ограничения на значения управляемых параметров, показатели исхода операции, связи показателей исхода операции с существенными параметрами, критерий эффективности. После внесения изменений в модель вновь выполняется оценка адекватности. 5. Оптимизация модели. Сущность оптимизации моделей состоит в их упрощении при заданном уровне адекватности. Основными показателями, по которым возможна оптимизация модели, выступают время и затраты средств для проведения исследований на ней. В основе оптимизации лежит возможность преобразования моделей из одной формы в другую. Преобразование может выполняться либо с использованием математических методов, либо эвристическим путем. Вопрос №15 Ввиду разнообразия применяемых математических моделей, их общая классификация затруднена. В литературе обычно приводят классификации, в основу которых положены различные подходы. Один из таких подходов связан с характером моделируемого процесса, когда выделяют детерминированные и вероятностные модели. Наряду с такой широко распространенной классификацией математических моделей существуют и другие. Математические модели с сосредоточенными параметрами. Обычно с помощью таких моделей описывают динамику систем, состоящих из дискретных элементов. С математической стороны - это системы обыкновенных линейных или нелинейных дифференциальных уравнений. Математические модели с распределенными параметрами
Математические модели, основанные на экстремальных принципах. Основной принцип классификации математических моделей
По форме представления математических моделей различают инвариантную, алгоритмическую, аналитическую и графическую модели объекта проектирования. В инвариантной форме математическая модель представляется системой уравнений вне связи с методом решения этих уравнений. В алгоритмической форме соотношения модели связаны с выбранным численным методом решения и записаны в виде алгоритма - последовательности вычислений. Среди алгоритмических моделей выделяют имитационные, модели предназначенные для имитации физических и информационных процессов, протекающих в объекте при его функционировании под воздействием различных факторов внешней среды. Аналитическая модель представляет собой явные зависимости искомых переменных от заданных величин (обычно зависимости выходных параметров объекта от внутренних и внешних параметров). Такие модели получают на основе физических законов, либо в результате прямого интегрирования исходных дифференциальных уравнений. Аналитические математические модели позволяют легко и просто решать задачи определения оптимальных параметров. Поэтому, если представляется возможность получения модели в таком виде, ее всегда целесообразно реализовать, даже если при этом придется выполнить ряд вспомогательных процедур, Такие модели обычно получают методом планирования эксперимента (вычислительного или физического).
Вопрос №16 Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием. Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы. Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующих систему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи. Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального). В общей постановке задача линейного программирования выглядит следующим образом: Имеются какие-то переменные х = (х1, х2, … хn) и функция этих переменных f(x) = f (х1, х2, … хn), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G:
В зависимости от вида функции f(x) и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что Математическая модель любой задачи линейного программирования включает в себя: · максимум или минимум целевой функции (критерий оптимальности); · систему ограничений в форме линейных уравнений и неравенств; · требование неотрицательности переменных.
Правило приведения ЗЛП к каноническому виду: 1. Если в исходной задаче некоторое ограничение (например, первое) было неравенством, то оно преобразуется в равенство, введением в левую часть некоторой неотрицательной переменной, при чем в неравенства «≤» вводится дополнительная неотрицательная переменная со знаком «+»; в случаи неравенства «≥» - со знаком «-»
Вводим переменную
Тогда неравенство (2.10) запишется в виде:
В каждое из неравенств вводится своя “ уравнивающая ” переменная, после ч
|
||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.161.199 (0.016 с.) |

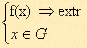
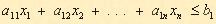
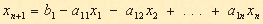 .
.



