

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Методы расчета параметров сетевой модели
Похожие статьи вашей тематики
В числе параметров сетевой модели, которые необходимо рассчитать, можно назвать продолжительность критического пути и критических работ, ранние и поздние сроки выполнения работ, ранние и поздние сроки свершения событий, резервы времени некритических работ. Следовательно, расчет сетевого графика заключается в расчете его параметров. Они могут быть получены по формулам (аналитический способ расчета), с помощью таблиц, непосредственно на графике или на базе ЭВМ.
Временные параметры сетевых графиков
Ранний срок окончания работы определяется по формуле:  
Поздний срок окончания работы определяется соотношением: t  (i,j)= (i,j)= 
А поздний срок начала этой работы – соотношением t  (i,j)= (i,j)= 
Полный резерв работы вычисляем по формуле: 
Частный резерв времени вычисляем по формуле:  
Свободный резерв времени вычисляем по формуле: 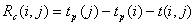 
Независимый резерв времени вычисляем по формуле: 
Критический путь
Сетевая модель сама по себе не может служить средством управления комплексом работ. Для управления комплексом работ с помощью сетевого графика необходимо располагать количественными оценками элементов сети - параметрами. Рассмотрим временн  е параметры сетевых графиков, включающие параметры событий и работ. Будем считать, что для каждой работы (i, j) задано время (продолжительность) ее выполнения - е параметры сетевых графиков, включающие параметры событий и работ. Будем считать, что для каждой работы (i, j) задано время (продолжительность) ее выполнения -  . .
При расчете параметров сети используется понятие пути. Последовательность работ, приводящая от одного события к другому и в которой каждая работа встречается не более одного раза, составляет путь. Полный путь - это путь от начального события до конечного. Продолжительность пути определяется суммой продолжительностей составляющих его работ. Полный путь, имеющий максимальную длину, называют критическим и обозначают Lкр, а его продолжительность tкр. Работы, принадлежащие критическому пути, называются критическим. Критический путь определяет общую продолжительность всего комплекса работ в целом. Изменение продолжительности работ, лежащих на критическом пути, может привести к сокращению или удлинению срока наступления конечного события, т.е. даты достижения конечной цели, определенной при планировании. Сетевой график может иметь несколько критических путей.
Соответственно в сетевом графике могут быть полные пути, которые либо вообще не совпадают с критическими, либо совпадают с ним частично. По продолжительности они меньше критического и поэтому называются ненапряженными. Ненапряженные пути обладают важным свойством: на участках, не совпадающих с критической последовательностью работ, они имеют резервы времени. Резерв времени ненапряженного пути определяется по формуле
 . .
Он показывает, на сколько в сумме могут быть увеличены продолжительности всех работ, принадлежащих этому пути. Если затянуть выполнение работ, лежащих на этом пути, на время большее чем R(L), то критический путь переместится на путь L.
| 25.
Поиск кратчайшего пути во взвешенном графе\Алгоритм Дейкстры
| Дан простой взвешенный граф G(V,E) без петель и дуг отрицательного веса. Найти кратчайшие пути от некоторой вершины a графа G до всех остальных вершин этого графа.
Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до a. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.
В качестве вышеописанных меток заведем массив D, для которого D[i] – кратчайшее на данном шаге расстояние до вершины i. Метка самой вершины a полагается равной 0, метки остальных вершин изначально заполняются а -ой строкой матрицы смежности, в которой бесконечностью (числом, заведомо большим самой большой исходной величины) обозначается отсутствие ребра или же все метки делаются бесконечными. Это означает то, что расстояния от a до других вершин пока неизвестны. Все вершины графа помечаются как непосещенные, а именно, заносятся в созданное нами множество вершин. По мере просмотра мы будем удалять их оттуда, тем самым отмечая их как просмотренные.
Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае из ещё не посещенных вершин (из нашего множества) выбирается вершина u, имеющая минимальную метку (расстояние до стартовой вершины). Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом, то есть просматриваем все вершины, которые есть в множестве и которые смежны с u. Вершины, соединенные с вершиной u ребрами, назовем соседями этой вершины. Для каждого соседа рассмотрим новую длину пути, равную сумме текущей метки для u и длины ребра, соединяющего u с этим соседом. Если полученная длина меньше метки соседа, заменим метку этой длиной. Рассмотрев всех соседей, пометим вершину u как посещенную и повторим шаг. Описанный выше процесс «обновления» метки для вершины назовем релаксацией.
Рассмотрим выполнение алгоритма на примере графа, показанного на рисунке. Пусть требуется найти расстояния от 1-й вершины до всех остальных. 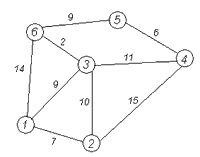
 Кружками обозначены вершины, линиями — пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначена их длина. Рядом с каждой вершиной красным будет обозначена метка — длина кратчайшего пути в эту вершину из вершины 1. Изначально это будет бесконечность, но, как уже говорилось, изначально можно заполнять D из строки a матрицы mass, это дело вкуса. В программной реализации (см. справа) заполнение будет осуществлено по второму принципу.
Первый шаг. Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6. Кружками обозначены вершины, линиями — пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначена их длина. Рядом с каждой вершиной красным будет обозначена метка — длина кратчайшего пути в эту вершину из вершины 1. Изначально это будет бесконечность, но, как уже говорилось, изначально можно заполнять D из строки a матрицы mass, это дело вкуса. В программной реализации (см. справа) заполнение будет осуществлено по второму принципу.
Первый шаг. Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6.
 Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна кратчайшему расстоянию до вершины 1 + длина ребра, идущего из 1 в 2, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, поэтому новая метка 2-й вершины равна 7.
Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна кратчайшему расстоянию до вершины 1 + длина ребра, идущего из 1 в 2, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, поэтому новая метка 2-й вершины равна 7.
 Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.
Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.
 Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Дейкстра, поэтому этот алгоритм носит его имя). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена (в программной реализации это будет удаление из множества не просмотренных вершин).
Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Дейкстра, поэтому этот алгоритм носит его имя). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена (в программной реализации это будет удаление из множества не просмотренных вершин).
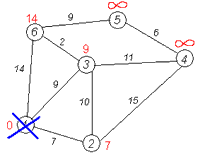 Второй шаг. Первый шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин, метка которых минимальна. Это вершина 2 с меткой 7.
Второй шаг. Первый шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин, метка которых минимальна. Это вершина 2 с меткой 7.
 Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю. Соседями вершины 2 являются 1, 3, 4. Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем. Следующий сосед вершины 2 — вершина 3. Если идти в неё через 2, то длина такого пути будет = 7 + 10 = 17. Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.
Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю. Соседями вершины 2 являются 1, 3, 4. Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем. Следующий сосед вершины 2 — вершина 3. Если идти в неё через 2, то длина такого пути будет = 7 + 10 = 17. Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.
 Ещё один сосед вершины 2 — вершина 4. Если идти в неё через 2-ю, то длина такого пути будет = кратчайшее расстояние до 2 + расстояние между вершинами 2 и 4 = 7 + 15 = 22. Поскольку 22 меньше бесконечности, устанавливаем метку вершины 4 равной 22.
Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещенную.
Ещё один сосед вершины 2 — вершина 4. Если идти в неё через 2-ю, то длина такого пути будет = кратчайшее расстояние до 2 + расстояние между вершинами 2 и 4 = 7 + 15 = 22. Поскольку 22 меньше бесконечности, устанавливаем метку вершины 4 равной 22.
Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещенную.
 Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты:
Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты:
 Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин (Это будут по порядку 6, 4 и 5).
Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин (Это будут по порядку 6, 4 и 5).
 Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда вычеркнуты все вершины. Результат его работы виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.
Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда вычеркнуты все вершины. Результат его работы виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.
 Рис. 7.22. Простой взвешенный орграф
Рассмотрим пример поиска кратчайшего пути на графе, представленного на рис. 7.22. Процесс назначения меток вершинам графа на каждом шаге удобно представить в виде таблицы рис. 7.23. Квадратами выделены окончательные метки, т.е. расстояния от них до x0. По такой таблице легко восстановить путь перемещения от z к x0, который отмечен ломаной кривой.
Рис. 7.22. Простой взвешенный орграф
Рассмотрим пример поиска кратчайшего пути на графе, представленного на рис. 7.22. Процесс назначения меток вершинам графа на каждом шаге удобно представить в виде таблицы рис. 7.23. Квадратами выделены окончательные метки, т.е. расстояния от них до x0. По такой таблице легко восстановить путь перемещения от z к x0, который отмечен ломаной кривой.
 Рис. 7.23. Результаты вычислений кратчайшего пути
26. Алгоритм Форда-Фалкерсона
Идея алгоритма заключается в следующем. Выбираем такой путь от ис-
точника с к стоку, чтобы для каждого ребра остаточная пропускная спо-
собность была строго больше нуля. При этом ребра на данном пути могут
проходиться как в прямом, так и в обратном направлении. Выбираем ми-
нимальное значение среди остаточных пропускных способностей ребер
данного пути. Увеличиваем поток на каждом из ребер данного пути на
выбранное минимальное значение. Далее ищем следующий аналогичный
путь.
Работа алгоритма продолжается до тех пор, пока удается находить
данные пути.
Сразу отметим, что данный алгоритм относится к классу недетерми-
нированных, т.е. каждый следующий шаг алгоритма определен неодно-
значно. И время работы (количество шагов) алгоритма зависит от того,
как будут выбираться шаги.
Шаги алгоритма будут отображаться пометками на графе и в специ-
альной таблице.
Каждый шаг отображается на графе пометками вида n)x=y, где n -
номер шага, x - максимальная пропускная способность ребра (не меня-
ется по ходу алгоритма), y - поток на ребре на данном шаге.
Таблица имеет 4 колонки:
1. Номер шага
2. Путь
3. Остаточные пропускные способности (ОПС) на данном пути
4. Минимальная остаточная пропускная способность на данном пути
ТИПО АЛГОРИТМ:
Потоком в сети называется некоторая функция, которая ставит в соответствие дуге некоторое число-вес дуги.
Для определения потока в сети используют алгоритм Форда-Фалкерсона:
а) ищем любую цепь из истока графа в сток;
б) каждой дуге приписываем возможный больший поток из истока в сток (записываем его через дробь с весом дуги; при этом поток не может превысить вес дуги, но может быть ему равен);
в) если поток становится равен весу дуги, то эта дуга является насыщенной, то есть через нее нельзя пройти при рассмотрении цепей в графе;
г) так перебираем все возможные цепи, пока станет невозможно попасть из истока в сток;
д) поток в сети будет равен сумме потоков всех дуг, инцидентных стоку графа (следует заметить, что сумма потоков всех дуг, инцидентных стоку графа равна сумме потоков всех дуг, инцидентных истоку графа).
27.
Матрица Кирхгофа
Матрица Кирхгофа (англ. Laplacian matrix) — одно из представлений графа с помощью матрицы. Матрица Кирхгофа используется для подсчета остовных деревьев данного графа (матричная теорема о деревьях), а также в спектральной теории графов.
Пример матрицы Кирхгофа простого графа.
Рис. 7.23. Результаты вычислений кратчайшего пути
26. Алгоритм Форда-Фалкерсона
Идея алгоритма заключается в следующем. Выбираем такой путь от ис-
точника с к стоку, чтобы для каждого ребра остаточная пропускная спо-
собность была строго больше нуля. При этом ребра на данном пути могут
проходиться как в прямом, так и в обратном направлении. Выбираем ми-
нимальное значение среди остаточных пропускных способностей ребер
данного пути. Увеличиваем поток на каждом из ребер данного пути на
выбранное минимальное значение. Далее ищем следующий аналогичный
путь.
Работа алгоритма продолжается до тех пор, пока удается находить
данные пути.
Сразу отметим, что данный алгоритм относится к классу недетерми-
нированных, т.е. каждый следующий шаг алгоритма определен неодно-
значно. И время работы (количество шагов) алгоритма зависит от того,
как будут выбираться шаги.
Шаги алгоритма будут отображаться пометками на графе и в специ-
альной таблице.
Каждый шаг отображается на графе пометками вида n)x=y, где n -
номер шага, x - максимальная пропускная способность ребра (не меня-
ется по ходу алгоритма), y - поток на ребре на данном шаге.
Таблица имеет 4 колонки:
1. Номер шага
2. Путь
3. Остаточные пропускные способности (ОПС) на данном пути
4. Минимальная остаточная пропускная способность на данном пути
ТИПО АЛГОРИТМ:
Потоком в сети называется некоторая функция, которая ставит в соответствие дуге некоторое число-вес дуги.
Для определения потока в сети используют алгоритм Форда-Фалкерсона:
а) ищем любую цепь из истока графа в сток;
б) каждой дуге приписываем возможный больший поток из истока в сток (записываем его через дробь с весом дуги; при этом поток не может превысить вес дуги, но может быть ему равен);
в) если поток становится равен весу дуги, то эта дуга является насыщенной, то есть через нее нельзя пройти при рассмотрении цепей в графе;
г) так перебираем все возможные цепи, пока станет невозможно попасть из истока в сток;
д) поток в сети будет равен сумме потоков всех дуг, инцидентных стоку графа (следует заметить, что сумма потоков всех дуг, инцидентных стоку графа равна сумме потоков всех дуг, инцидентных истоку графа).
27.
Матрица Кирхгофа
Матрица Кирхгофа (англ. Laplacian matrix) — одно из представлений графа с помощью матрицы. Матрица Кирхгофа используется для подсчета остовных деревьев данного графа (матричная теорема о деревьях), а также в спектральной теории графов.
Пример матрицы Кирхгофа простого графа.
| Помеченный граф
| Матрица Кирхгофа
| 
| 
|
Известным способом расчета потенциалов узлов является использование матрицы Кирхгофа. При таком способе потенциал i -го узла  определяется как кофактор (алгебраическое дополнение) матрицы Кирхгофа для i -го элемента. определяется как кофактор (алгебраическое дополнение) матрицы Кирхгофа для i -го элемента.
Сама матрица Кирхгофа определяется следующим образом - диагональные элементы представляют собой сумму элементов матрицы проводимостей по соответствующему столбцу (колонке), недиагональные - элементы матрицы проводимостей, взятые с отрицательным знаком.
Таким образом для матрицы проводимостей

матрица Кирхгофа будет равна:

Определитель матрицы Кирхгофа равен нулю.
Для вычисления потенциала первого узла  необходимо рассчитать определитель от минора матрицы Кирхгофа: необходимо рассчитать определитель от минора матрицы Кирхгофа:
 . .
Раскрывая определитель, получаем:

| (4)
| Выражения для  и и  можно также рассчитать по матрице Кирхгофа, а можно получить из (4) перестановкой индексов (1-2), (1-3). можно также рассчитать по матрице Кирхгофа, а можно получить из (4) перестановкой индексов (1-2), (1-3).
Особенности аналитического выражения потенциала узла U
1. Потенциал представляет собой сумму кортежей - произведений весов ребер. Количество множителей в кортеже зависит от размерности графа, - при 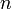 узлах размерность кортежа будет узлах размерность кортежа будет  . Количество самих кортежей . Количество самих кортежей  связано с связано с 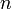 степенной зависимостью (формула Кэли): степенной зависимостью (формула Кэли):

§ Например, для графа из пяти вершин количество кортежей в выражении для потенциала составит  . .
2. Потенциал i-го узла не зависит от весов  исходящих из него ребер ( исходящих из него ребер ( не зависит от не зависит от  и и  ). ).
3. Кортеж состоит из весов ребер, которые исходят из разных узлов (из всех узлов, кроме рассчитываемого). В одном кортеже нет ребер, исходящих из одного узла.
4. В каждом кортеже обязательно присутствует вес ребра, входящего в рассчитываемый узел.
5. В выражении для потенциала не должно содержаться кортежей, образующих циклы.
§ Примеры циклических кортежей:  и т.д. и т.д.
Алгоритм Крускала
В любой момент работы алгоритма Крускала множество А выбранных рёбер (часть будущего остова) не содержит циклов. Оно соединяет вершины графа в несколько связных компонент, каждая из которых является деревом. Среди всех рёбер, соединяющих вершины из разных компонент, берётся ребро наименьшего веса. Надо проверить, что оно является безопасным.
Пусть (u, v) — такое ребро, соединяющее вершины из компонент С1 и C2- Это ребро является лёгким ребром для разреза (С1, V \C1).
Реализация алгоритма Крускала использует структуры данных для непересекающихся множеств. Элементами множеств являются вершины графа.
Алгоритм Прима
Как и алгоритм Крускала, алгоритм Прима следует общей схеме алгоритма построения минимального остова. В этом алгоритме растущая часть остова представляет собой дерево (множество рёбер которого есть А). Формирование дерева начинается с произвольной корневой вершины r. На каждом шаге добавляется ребро наименьшего веса среди рёбер соединяющих вершины этого дерева с вершинами не из дерева. По следствию такие рёбра являются безопасными для А, так что в результате получается минимальный остов.
При реализации важно быстро выбирать лёгкое ребро. Алгоритм получает на вход связный граф G и корень r минимального покрывающего дерева. В ходе алгоритма все вершины, ещё не попавшие в дерево, хранятся в очереди с приоритетами. Приоритет вершины v определяется значением [u], которое равно минимальному весу рёбер, соединяющих v с вершинами дерева А. Поле[v] для вершин дерева указывает на родителя, а для вершины v Q указывает на вершину дерева, в которую ведёт ребро веса [v] (одно из таких рёбер, если их несколько). Мы не храним множество А вершин строимого дерева явно; его можно восстановить как
A = {(v, [v]):v V \{r} \Q}.
В конец работы алгоритма очередь Q пуста, и множество
A = {(v, [v]):v V \{r}}.
есть множество ребер покрывающего дерева.
|
|





 (i,j)=
(i,j)= 
 (i,j)=
(i,j)= 


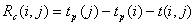

 е параметры сетевых графиков, включающие параметры событий и работ. Будем считать, что для каждой работы (i, j) задано время (продолжительность) ее выполнения -
е параметры сетевых графиков, включающие параметры событий и работ. Будем считать, что для каждой работы (i, j) задано время (продолжительность) ее выполнения -  .
. .
.
 Кружками обозначены вершины, линиями — пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначена их длина. Рядом с каждой вершиной красным будет обозначена метка — длина кратчайшего пути в эту вершину из вершины 1. Изначально это будет бесконечность, но, как уже говорилось, изначально можно заполнять D из строки a матрицы mass, это дело вкуса. В программной реализации (см. справа) заполнение будет осуществлено по второму принципу.
Первый шаг. Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6.
Кружками обозначены вершины, линиями — пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначена их длина. Рядом с каждой вершиной красным будет обозначена метка — длина кратчайшего пути в эту вершину из вершины 1. Изначально это будет бесконечность, но, как уже говорилось, изначально можно заполнять D из строки a матрицы mass, это дело вкуса. В программной реализации (см. справа) заполнение будет осуществлено по второму принципу.
Первый шаг. Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6.
 Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна кратчайшему расстоянию до вершины 1 + длина ребра, идущего из 1 в 2, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, поэтому новая метка 2-й вершины равна 7.
Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна кратчайшему расстоянию до вершины 1 + длина ребра, идущего из 1 в 2, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, поэтому новая метка 2-й вершины равна 7.
 Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.
Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.
 Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Дейкстра, поэтому этот алгоритм носит его имя). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена (в программной реализации это будет удаление из множества не просмотренных вершин).
Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Дейкстра, поэтому этот алгоритм носит его имя). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена (в программной реализации это будет удаление из множества не просмотренных вершин).
 Второй шаг. Первый шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин, метка которых минимальна. Это вершина 2 с меткой 7.
Второй шаг. Первый шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин, метка которых минимальна. Это вершина 2 с меткой 7.
 Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю. Соседями вершины 2 являются 1, 3, 4. Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем. Следующий сосед вершины 2 — вершина 3. Если идти в неё через 2, то длина такого пути будет = 7 + 10 = 17. Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.
Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю. Соседями вершины 2 являются 1, 3, 4. Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем. Следующий сосед вершины 2 — вершина 3. Если идти в неё через 2, то длина такого пути будет = 7 + 10 = 17. Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.
 Ещё один сосед вершины 2 — вершина 4. Если идти в неё через 2-ю, то длина такого пути будет = кратчайшее расстояние до 2 + расстояние между вершинами 2 и 4 = 7 + 15 = 22. Поскольку 22 меньше бесконечности, устанавливаем метку вершины 4 равной 22.
Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещенную.
Ещё один сосед вершины 2 — вершина 4. Если идти в неё через 2-ю, то длина такого пути будет = кратчайшее расстояние до 2 + расстояние между вершинами 2 и 4 = 7 + 15 = 22. Поскольку 22 меньше бесконечности, устанавливаем метку вершины 4 равной 22.
Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещенную.
 Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты:
Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты:
 Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин (Это будут по порядку 6, 4 и 5).
Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин (Это будут по порядку 6, 4 и 5).
 Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда вычеркнуты все вершины. Результат его работы виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.
Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда вычеркнуты все вершины. Результат его работы виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.
 Рис. 7.22. Простой взвешенный орграф
Рассмотрим пример поиска кратчайшего пути на графе, представленного на рис. 7.22. Процесс назначения меток вершинам графа на каждом шаге удобно представить в виде таблицы рис. 7.23. Квадратами выделены окончательные метки, т.е. расстояния от них до x0. По такой таблице легко восстановить путь перемещения от z к x0, который отмечен ломаной кривой.
Рис. 7.22. Простой взвешенный орграф
Рассмотрим пример поиска кратчайшего пути на графе, представленного на рис. 7.22. Процесс назначения меток вершинам графа на каждом шаге удобно представить в виде таблицы рис. 7.23. Квадратами выделены окончательные метки, т.е. расстояния от них до x0. По такой таблице легко восстановить путь перемещения от z к x0, который отмечен ломаной кривой.
 Рис. 7.23. Результаты вычислений кратчайшего пути
26. Алгоритм Форда-Фалкерсона
Идея алгоритма заключается в следующем. Выбираем такой путь от ис-
точника с к стоку, чтобы для каждого ребра остаточная пропускная спо-
собность была строго больше нуля. При этом ребра на данном пути могут
проходиться как в прямом, так и в обратном направлении. Выбираем ми-
нимальное значение среди остаточных пропускных способностей ребер
данного пути. Увеличиваем поток на каждом из ребер данного пути на
выбранное минимальное значение. Далее ищем следующий аналогичный
путь.
Работа алгоритма продолжается до тех пор, пока удается находить
данные пути.
Сразу отметим, что данный алгоритм относится к классу недетерми-
нированных, т.е. каждый следующий шаг алгоритма определен неодно-
значно. И время работы (количество шагов) алгоритма зависит от того,
как будут выбираться шаги.
Шаги алгоритма будут отображаться пометками на графе и в специ-
альной таблице.
Каждый шаг отображается на графе пометками вида n)x=y, где n -
номер шага, x - максимальная пропускная способность ребра (не меня-
ется по ходу алгоритма), y - поток на ребре на данном шаге.
Таблица имеет 4 колонки:
1. Номер шага
2. Путь
3. Остаточные пропускные способности (ОПС) на данном пути
4. Минимальная остаточная пропускная способность на данном пути
ТИПО АЛГОРИТМ:
Потоком в сети называется некоторая функция, которая ставит в соответствие дуге некоторое число-вес дуги.
Для определения потока в сети используют алгоритм Форда-Фалкерсона:
а) ищем любую цепь из истока графа в сток;
б) каждой дуге приписываем возможный больший поток из истока в сток (записываем его через дробь с весом дуги; при этом поток не может превысить вес дуги, но может быть ему равен);
в) если поток становится равен весу дуги, то эта дуга является насыщенной, то есть через нее нельзя пройти при рассмотрении цепей в графе;
г) так перебираем все возможные цепи, пока станет невозможно попасть из истока в сток;
д) поток в сети будет равен сумме потоков всех дуг, инцидентных стоку графа (следует заметить, что сумма потоков всех дуг, инцидентных стоку графа равна сумме потоков всех дуг, инцидентных истоку графа).
27.
Матрица Кирхгофа
Матрица Кирхгофа (англ. Laplacian matrix) — одно из представлений графа с помощью матрицы. Матрица Кирхгофа используется для подсчета остовных деревьев данного графа (матричная теорема о деревьях), а также в спектральной теории графов.
Пример матрицы Кирхгофа простого графа.
Рис. 7.23. Результаты вычислений кратчайшего пути
26. Алгоритм Форда-Фалкерсона
Идея алгоритма заключается в следующем. Выбираем такой путь от ис-
точника с к стоку, чтобы для каждого ребра остаточная пропускная спо-
собность была строго больше нуля. При этом ребра на данном пути могут
проходиться как в прямом, так и в обратном направлении. Выбираем ми-
нимальное значение среди остаточных пропускных способностей ребер
данного пути. Увеличиваем поток на каждом из ребер данного пути на
выбранное минимальное значение. Далее ищем следующий аналогичный
путь.
Работа алгоритма продолжается до тех пор, пока удается находить
данные пути.
Сразу отметим, что данный алгоритм относится к классу недетерми-
нированных, т.е. каждый следующий шаг алгоритма определен неодно-
значно. И время работы (количество шагов) алгоритма зависит от того,
как будут выбираться шаги.
Шаги алгоритма будут отображаться пометками на графе и в специ-
альной таблице.
Каждый шаг отображается на графе пометками вида n)x=y, где n -
номер шага, x - максимальная пропускная способность ребра (не меня-
ется по ходу алгоритма), y - поток на ребре на данном шаге.
Таблица имеет 4 колонки:
1. Номер шага
2. Путь
3. Остаточные пропускные способности (ОПС) на данном пути
4. Минимальная остаточная пропускная способность на данном пути
ТИПО АЛГОРИТМ:
Потоком в сети называется некоторая функция, которая ставит в соответствие дуге некоторое число-вес дуги.
Для определения потока в сети используют алгоритм Форда-Фалкерсона:
а) ищем любую цепь из истока графа в сток;
б) каждой дуге приписываем возможный больший поток из истока в сток (записываем его через дробь с весом дуги; при этом поток не может превысить вес дуги, но может быть ему равен);
в) если поток становится равен весу дуги, то эта дуга является насыщенной, то есть через нее нельзя пройти при рассмотрении цепей в графе;
г) так перебираем все возможные цепи, пока станет невозможно попасть из истока в сток;
д) поток в сети будет равен сумме потоков всех дуг, инцидентных стоку графа (следует заметить, что сумма потоков всех дуг, инцидентных стоку графа равна сумме потоков всех дуг, инцидентных истоку графа).
27.
Матрица Кирхгофа
Матрица Кирхгофа (англ. Laplacian matrix) — одно из представлений графа с помощью матрицы. Матрица Кирхгофа используется для подсчета остовных деревьев данного графа (матричная теорема о деревьях), а также в спектральной теории графов.
Пример матрицы Кирхгофа простого графа.


 определяется как кофактор (алгебраическое дополнение) матрицы Кирхгофа для i -го элемента.
определяется как кофактор (алгебраическое дополнение) матрицы Кирхгофа для i -го элемента.

 необходимо рассчитать определитель от минора матрицы Кирхгофа:
необходимо рассчитать определитель от минора матрицы Кирхгофа: .
.
 и
и  можно также рассчитать по матрице Кирхгофа, а можно получить из (4) перестановкой индексов (1-2), (1-3).
можно также рассчитать по матрице Кирхгофа, а можно получить из (4) перестановкой индексов (1-2), (1-3).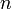 узлах размерность кортежа будет
узлах размерность кортежа будет  . Количество самих кортежей
. Количество самих кортежей  связано с
связано с 
 .
. исходящих из него ребер (
исходящих из него ребер ( и
и  ).
). и т.д.
и т.д.


