
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экономические приложения задачи линейного программирования.Содержание книги
Поиск на нашем сайте
Основная задача народнохозяйственного планирования: х= (хj) – объемы производства в отраслях народного хозяйства (т, шт. и т.д.) у – объем удовлетворения потребностей (коэффициент). Целевая функция: max y Балансы невоспроизводимых ресурсов: А1х≤b Балансы воспроизводимых ресурсов: А2х≤0 Баланс продукции: А3х≥ус; х≥0, у≥0. Где: А1 – матрица потребности в ресурсах для обеспечения единичного объема производства в каждой отрасли; строки – ресурсы, столбцы – отрасли. b – объемы непроизводственных ресурсов (земельные угодья, трудовые ресурсы, запасы полезных ископаемых и т.д.), имеющиеся в распоряжении народного хозяйства. А2 – матрица затрат (+) и выпуска (-) ресурсов при единичном объеме производства в каждой отрасли; строки – ресурсы, столбцы – отрасли. 0 – вектор, состоящий из 0 А3 – матрица выпуска(+) конечной продукции при единичном объеме производства в каждой отрасли; строки – виды продукции, столбцы – отрасли с- вектор объемов потребления каждого вида конечной продукции при единичном (стандартном) уровне удовлетворения потребностей Основная задача производственного планирования х= (хj) – объемы реализации продукции (т, шт. и т.д.) у= (ук) – объемы закупки ресурсов (т, шт. и т.д.) Целевая функция: max c1x – c2y Балансы ресурсов (например, работники, производственные помещения, оборудование, сырье, электроэнергия и т.д.): A1x ≤ y + b1 Выполнение обязательств (например, налог на имущество, возврат инвестиционного кредита и т.д.): A2x ≤ b2 х≥0, у≥0. Где: c1 – вектор цен продукции (за вычетом НДС), руб./ед. c2 – вектор цен ресурсов (включая НДС), руб./ед. A1 – матрица затрат ресурсов на производство и реализацию единицы продукции, ед.рес./ед.прод. b1 – вектор наличия (начальных запасов) ресурсов A2 – матрица объемов обязательств, выполняемых вследствие реализации единицы продукции каждого вида b2 – объемы обязательств, имеющихся у предприятия и учитываемых при оптимальном планировании (выполнение которых зависит от составленного плана).
n Два способа установки XA u Если есть права доступа к каталогу C:\WINDOWS t копируем туда файлы CXA32.DLL и CAXA32.DLL u Иначе t t после вызова файла модели нажимаем кнопку
• это действие повторяется при каждом вызове Excel n Антивирус Касперского блокирует выполнение XA t При первом вызове программы следует в ответ на предупреждение антивируса дать ему указание разрешать выполнение данной программы
22. - 21 Неопределенность — это неполнота или недостоверность информации об условиях реализации решения, наличие фактора случайности или противодействия. Таким образом, принятие решения в условиях неопределенности означает выбор варианта решения, когда одно или несколько действий имеют своим следствием множество частных исходов, но их вероятности совершенно не известны или не имеют смысла. Ситуация полной неопределенности характеризуется отсутствием какой бы то ни было дополнительной информации. Какие же существуют правила-рекомендации по принятию решений в этой ситуации? Для выбора оптимальной стратегии в ситуации неопределённости используются различные правила и критерии. Правило максимин (критерий Ваальда). В соответствии с этим правилом из альтернатив aj выбирают ту, которая при самом неблагоприятном состоянии внешней среды, имеет наибольшее значение показателя. С этой целью в каждой строчке матрицы фиксируют альтернативы с минимальным значением показателя и из отмеченных минимальных выбирают максимальное. Альтернативе а* с максимальным значением из всех минимальных даётся приоритет. Принимающий решение в этом случае минимально готов к риску, предполагая максимум негативного развития состояния внешней среды и учитывая наименее благоприятное развитие для каждой альтернативы. По критерию Ваальда лица, принимающие решения, выбирают стратегию, гарантирующую максимальное значение наихудшего выигрыша (критерия максимина). Правило максимакс В соответствии с этим правилом выбирается альтернатива с наивысшим достижимым значением оцениваемого показателя. При этом ЛПР не учитывает риска от неблагоприятного изменения окружающей среды. Альтернатива находится по формуле: а* = {аjmaxj maxi Пij } Используя это правило, определяют максимальное значение для каждой строки и выбирают наибольшее из них. Большой недостаток правил максимакса и максимина – использование только одного варианта развития ситуации для каждой альтернативы при принятии решения. Правило минимакс (критерий Севиджа) В отличие от максимина минимакс ориентирован на минимизацию не столько потерь, сколько сожалений по поводу упущенной прибыли. Правило допускает разумный риск ради получения дополнительной прибыли. Критерий Севиджа рассчитывается по формуле: min max П = mini [ maxj (maxi Xij - Xij)] где mini, maxj – поиск максимума перебором соответствующих столбцов и строк. Расчёт минимакса состоит их четырёх этапов: 1. Находится лучший результат каждой графы в отдельности, то есть максимум Xij (реакции рынка). 2. Определяется отклонение от лучшего результата каждой отдельной графы, то есть maxi Xij – Xij. Полученные результаты образуют матрицу отклонений (сожалений), так как её элементы – это недополученная прибыль от неудачно принятых решений, допущенных из-за ошибочной оценки возможности реакции рынка. 3. Для каждой сточки сожалений находим максимальное значение. 4. Выбираем решение, при котором максимальное сожаление будет меньше других. Правило Гурвица В соответствии с этим правилом правила максимакс и максимин сочетаются связыванием максимума минимальных значений альтернатив. Это правило называют ещё правилом оптимизма – пессимизма. Оптимальную альтернативу можно рассчитать по формуле: а* = maxi [(1-α) minj Пji+ α maxj Пji] где α- коэффициент оптимизма, α =1…0 при α =1 альтернатива выбирается по правилу максимакс, при α =0 – по правилу максимин. Учитывая боязнь риска, целесообразно задавать α =0,3. Наибольшее значение целевой величины и определяет необходимую альтернативу. Правило Гурвица применяют, учитывая более существенную информацию, чем при использовании правил максимин и максимакс. Таким образом, при принятии управленческого решения в общем случае необходимо:
21. положение называется частичной неопределенностью, если известны вероятности того, что реальная ситуация развивается по варианту j. 23. Сетевая модель (сетевой график) – графическое изображение плана выполнения комплекса работ внешне напоминающая сеть, состоящую из стрелок (работ) и узлов (событий), которые отражают логическую взаимосвязь всех операций. Достоинства СПУ: 1. Формировать календарный план реализации некоторого комплекса работ; 2. Выявлять и мобилизовывать резервы времени, трудовые, материальные и денежные ресурсы; 3. Осуществлять управление комплексом работ и предупреждать возможность срывов в ходе работы; 4. Повышать эффективность управления в целом. Кроме того, события можно охарактеризовать как простые и сложные в зависимости от числа входящих в них и выходящих из них работ. Простым событием называется такое событие, в которое входит и из которого выходит только одна работа. В сложное событие входят или выходят две и более работ. Путъ — это последовательность работ, соединяющих начальную и конечную точки вершины. Критический путь - это полный путь, имеющий наибольшую продолжительность всех работ. Критическими называют работы и события, расположенные на критическом пути. Вначале планируемый процесс разбивается на отдельные работы, составляется перечень работ и событий, продумывается последовательность выполнения, оценивается продолжительность каждой работы, затем составляется сетевой график. Далее рассчитывается параметры событий, работ, определяются резервы времени и критический путь. Наконец проводятся анализ и оптимизация сетевого графика, который при необходимости вычерчивается заново с пересчетом параметров событий и работ., Упорядочение сетевого графика – заключается в таком расположении событий и работ при котором для любой работы предшествующей ей события расположены левее и имеет меньший размер по сравнению с завершающим эту работу событием. Другими словами все работы – стрелки, направлены слева направо, от событий с меньшими номерами к событиям с большими номерами. При построении сетевого графика сначала разрабатывают перечень событий, который определяют производственную задачу. Затем предусматривают работы, в результате которых все необходимые события должны произойти. 24.
|
||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 574; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.27.168 (0.01 с.) |

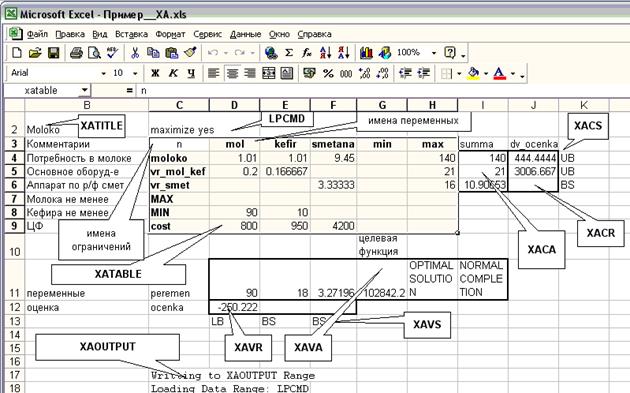
 копируем файлы CXA32.DLL и CAXA32.DLL в ту папку, в которой решаем модель
копируем файлы CXA32.DLL и CAXA32.DLL в ту папку, в которой решаем модель


