
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сетевое представление программы (сетевая модель)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сетевая модель отображает взаимосвязи между операциями и порядок их выполнения (отношение упорядочения или следования). Как правило, для представления операции используется стрелка (ориентированная дуга), направление которой соответствует процессу реализации программы во времени. Отношение упорядочения между операциями задается с помощью событий. Событие определяется как момент времени, когда завершаются одни операции и начинаются другие. Начальная и конечная точки любой операции описываются, таким образом, парой событий, которые обычно называют начальным событием и конечным событием. Операции, выходящие из некоторого события, не могут начаться, пока не будут завершены все операции, входящие в это событие. Протекание операций во времени задается путем нумерации событий, причем номер начального события всегда меньше номера конечного. Такой способ нумерации особенно удобен при выполнении вычислений на ЭВМ
Правила построения сетевой модели Правило 1. Каждая операция в сети представляется одной, только одной дугой (стрелкой). Ни одна из операций не должнa появляться в модели дважды. При этом следует различать случай, когда какая-либо операция разбивается на части; тогда каждая часть изображается отдельной дугой. Так, например, прокладку трубопровода можно расчленить на прокладку отдельных секций и рассматривать прокладку каждой секции как самостоятельную операцию. Правило 2. Ни одна пара операций не должна определяться одинаковыми начальным и конечным событиями. Возможность неоднозначного определения операций через события появляется в случае, когда две или большее число операций допустимо выполнять, одновременно. Чтобы исключить такую “ошибку” между A и конечным (начальным) событием или между В и конечным (начальным) событием вводится фиктивная операция. Рис.6.1(б) иллюстрирует различные варианты введения такой фиктивной операции D. В результате операции А и В определяются теперь однозначно парой событий, отличающихся либо номером начального, либо номером конечного события. Следует обратить внимание на то, что фиктивные операции не требуют затрат ни времени, ни ресурсов. Правило 3. При включении каждой операции в сетевую модель для обеспечения правильного упорядочения необходимо дать ответы на следующие вопросы.
а) Какие операции необходимо завершить непосредственно перед началом рассматриваемой операции? б) Какие операции должны непосредственно следовать после завершения данной операции? в) Какие операции могут выполняться одновременно с рассматриваемой?
Рис.6.1. Введение фиктивной операции
Эти правила позволяют проверять (перепроверять) отношения упорядочения в процессе построения сети.
Расчет сетевой модели
Применение методов СПУ в конечном счете должно обеспечить получение календарного плана, определяющего сроки начала и окончания каждой операции. Построение сети является лишь первым шагом на пути к достижению этой цели. Вследствие наличия взаимосвязей между различными операциями для определения сроков их начала и окончания необходимо проведение специальных расчетов. Эти расчеты можно выполнять непосредственно на сети, пользуясь простыми правилами. В результате вычислений определяются критические и некритические операции программы. Операция считается критической, если задержка ее начала приводит к увеличению срока окончания всей программы. Некритическая операция отличается тем, что промежуток времени между ее ранним началом и поздним окончанием (в рамках рассматриваемой программы) больше ее фактической продолжительности. В таком случае говорят, что некритическая операция имеет резерв, или запас, времени.
Определение критического пути
Критический путь определяет непрерывную последовательность критических операций, связывающих исходное и завершающее события сети. Другими словами, критический путь задает все критические операции программы. Метод определения такого пути иллюстрируется на численном примере. Пример. Рассмотрим сетевую модель, показанную на рис.6.2, с исходным событием 0 и завершающим событием 6. Оценки времени, необходимого для выполнения каждой операции, даны у стрелок.
Рис.6.2. Сетевая модель календарного плана
Расчет критического пути включает два этапа. Первый этап называется прямым проходом. Вычисления начинаются с исходного события и продолжаются до тех пор, пока не будет достигнуто завершающее событие всей сети. Для каждого события вычисляется одно число, представляющее ранний срок его наступления. Эти числа указаны на рис.6.2 в квадратах. На втором этапе, называемом обратным проходом, вычисления начинаются с завершающего события сети и продолжаются, пока не будет достигнуто исходное событие. Для каждого события вычисляется число, представляющее поздний срок его наступления. Эти числа даны в треугольниках.
Рассмотрим прямой проход. Пусть tрнi —ранний срок начала всех операций, выходящих из события i. Таким образом, tрнi, является также ранним сроком наступления cобытия i. Если принять i=0, т. е. считать, что номер исходного события сети равен нулю, то при расчете сети tрнo =0. Обозначим символом τ ij продолжительность операции (i, j). Тогда вычисления при прямом проходе выполняются по формуле tрнj=max{tрнi+τij} для всех операций (i,j), где tрнo==0. Следовательно, чтобы вычислить tрнj для события j, нужно сначала определить tрнi начальных событий всех операций (i, j), входящих в событие j. Применительно к рис.6.2 вычисления при прямом проходе начинаются с tрнo=0, как показано в квадрате над событием 0. Поскольку в событие 1 входит только одна операция (0, 1) продолжительностью τo1=2, tрнi=tрнo+ τ o1==0+2=2. Этот результат записан в квадрате у события 1. Рассмотрим далее событие 2. [Заметим, что событие 3 пока рассматривать нельзя, так как срок tрн2 (событие 2) еще неизвестен.] Таким образом, tрн2=tрн0+τ02=0+3=3. Поместим этот результат в квадрат у события 2. Перейдем теперь к событию 3. Поскольку в него входят две операции (1, 3) и (2, 3), tрн3 = max { tрнi + τi3} = max {2 + 2,3 + 3} = 6, i=1,2. Этот результат также записан в квадрате у события 3. Вычисления продолжаются аналогичным образом, пока не будут определены значения tрнj, для всех j. Имеем tрн4 = max {tрнi + τi4} = max {3 + 2,6 + 0} == 6, i=2, 3 tрн5 = max {tрнi + τi5} = max {6 + 3,6 + 7} == 13, i=3,4 tрн6 = max {tрнi + τi6} = max {б + 2,6 + 5,13 + 6} = 19, i=3, 4,6 На этом вычисления прямого прохода заканчиваются. Обратный проход начинается с завершающего события сети. При этом целью является определение tпоi; — поздних сроков окончания всех операций, входящих в событие i. Если принять i=n, где n — завершающее событие сети, то tпоn=tрнn является отправной точкой обратного прохода. В общем виде для любого события i tпоi=min{tпоj—τij} для всех операций (i, j). Значения tпо (указанные в треугольниках) вычисляются следующим образом: tпо6=tрн6==19, tпо5=tпо6 –τ56 = 19-3=13, tпо4=min {tпоj—τ4j}=min={13—7, 19—5}=6, i = 5,6 tпо3=min {tпоj—τ3j}=min{6—0, 13—3, 19—2} =6, i=4, 5, 6 tпо2=min {tпоj—τ2j}=min{6—3, 6—2}=3, i=3,4 tпо1 = tпо3—τ13 == 6 — 2 = 4, tпо0=min {tпоj—τ0j}==min{4—2, 3—3}==0, i=1,2 Вычисления при обратном проходе закончены. Теперь, используя результаты вычислений при прямом и обратном проходах, можно определить операции критического пути. Операция (i,j) принадлежиткритическому пути, если она удовлетворяет следующим трем условиям: tрнi=tпоi (1), tрнj=tпоj (2), tрнj—tрнi=tпоj—tпоi=τij (3). По существу, эти условия означают, что между ранним сроком начала (окончания) и поздним сроком начала (окончания) критической операции запас времени отсутствует. В сетевой модели это отражается в том, что для критических операций числа, проставленные в квадратах и треугольниках у начальных и конечных событий, совпадают, а разность между числом в квадрате (или треугольнике) у конечного события и числом у начального события равна продолжительности соответствующей операции в квадрате (или треугольнике).
На рис.6.2 критический путь включает операции (0, 2), (2, 3), (3, 4), (4, 5) и (5, 6). Критический путь определяет минимальную продолжительность всей программы в целом. Заметим, что операции (2, 4), (3, 5), (3, 6) и (4, 6) удовлетворяют условиям (1) и (2), но не условию (3). Поэтому они не являются критическими. Критический путь представляет собой непрерывную цепочку операций, соединяющую исходные события сети с завершающим. Определение резервов времени
При определении критического пути необходимо вычислить резервы времени для некритических операций. Очевидно, что резерв времени критической операции должен быть равен нулю. Поэтому она и называется критической. Прежде чем приступить к вычислению резервов времени, нужно ввести определения еще двух сроков, связанных с каждой операцией. Это срок позднего начала (tпн) и срок раннего окончания (tро), которые для любой операции (i, j) задаются соотношениями tпнij=tпоj—τij, tроij=tрнi+τij. Различают два основных вида резервов времени: полный резерв (r) и свободный резерв (ρ). Полный резерв времени операции (i,j) представляет собой разность между максимальным отрезком времени, в течение которого может быть выполнена операция (tпоj—tрнj), и ее продолжительностью τij, т. е. rij=tпоj—tрнj—τij=tпоj—tроij=tпнij—tрнi. Свободный резерв времени определяется в предположении, что все операции в сети начинаются в ранние сроки. При этом условии величина ρij для операции {i, j} представляет собой превышение допустимого отрезка времени (tрнj —tрнi) над продолжительностью операции (τij }, т. е. ρij =tрнj+tрнi-τij Результаты расчета критического пути и резервов времени некритических операций можно свести в удобную для пользования таблицу. В столбцах (1),(2),(3) и (6) приведены результаты расчета сети, рассмотренной в примере. Остальные данные легко вычислить по приведенным выше формулам. В таблице рис.6.3 приведены результаты типичного расчета сетевой модели. Она содержит всю необходимую для построения календарного плана (графика) информацию. Заметим, что только критические операции должны иметь нулевой полный резерв времени. Результаты расчета критического пути и резервов времени некритических операций можно свести в удобную для пользования таблицу, представленную на рис. 6.3. В столбцах (1),(2),(3) и (6) приведены результаты расчета рассмотренной сети. Остальные данные вычислены по приведенным выше формулам.
Таблица содержит всю необходимую информацию для построения календарного плана (графика). Заметим, что только критические операции должны иметь нулевой полный резерв времени. Когда полный резерв равен нулю, свободный резерв также должен быть равен нулю. Однако обратное неверно, поскольку свободный, резерв некритической операции также может быть нулевым. Так, например, свободный резерв времени некритической операции (0, 1) равен нулю.
Практическая работа №7
АНТАГОНИСТИЧЕСКИЕ ИГРЫ
Самым простым случаем, подробно разработанным в теории игр, является конечная парная игра с нулевой суммой, то есть игра, в которой противоборствуют две стороны А и В и выполнено условие Игроки А и В, имеют противоположные интересы: выигрыш одного равен проигрышу другого. Можно интересоваться только выигрышем игрока А. Естественно, что А хочет увеличить выигрыш, а В хочет его уменьшить. Пусть А имеет m возможных стратегий
Таблица 7.1. Матрица игры m*n
Если такая таблица составлена, то говорят, что игра приведена к матричной форме Предположим, что сторона А пытается найти наилучшую из своих стратегий, оценивая выигрыши При этом подходе отсутствует какой бы то ни было риск или расчет на возможные ошибки со стороны В. Если А будет придерживаться максиминной стратегии, то выиграет не меньше a, называемой нижней ценой игры или максиминным выигрышем. Предположим, что аналогичные рассуждения ведёт сторона В, но речь идет о проигрышах стороны А. Следовательно, произвольно взятая стратегия Оперирующие стороны могут использовать принцип гарантированного результата (минимакса) в качестве основы принятия решений и добиваться за счёт этого заранее предсказанных результатов.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 615; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.67.56 (0.01 с.) |

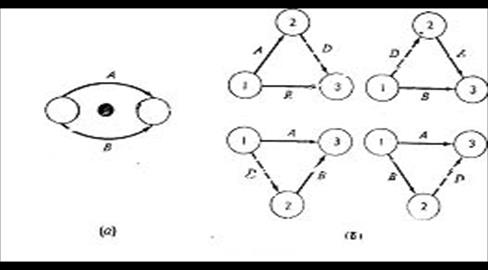
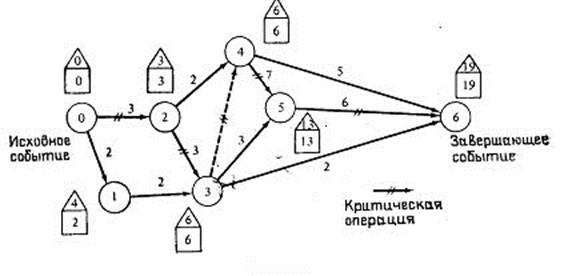
 Рис. 6.3. Итоговая таблица результатов расчетов календарного плана
Рис. 6.3. Итоговая таблица результатов расчетов календарного плана , т.е. все, что выигрывает А, проигрывает В, и наоборот. Такая игра называется антагонистической.
, т.е. все, что выигрывает А, проигрывает В, и наоборот. Такая игра называется антагонистической.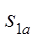 ,
,  ,...,
,..., 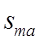 , а противник В – n, возможных стратегий
, а противник В – n, возможных стратегий  ,
,  ,...,
,...,  . Обозначим через
. Обозначим через  выигрыш стороны А, если она пользуется стратегией
выигрыш стороны А, если она пользуется стратегией 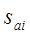 , а противник пользуется стратегией
, а противник пользуется стратегией  . В принципе мы можем составить прямоугольную матрицу, в которой перечислены стратегии игроков и соответствующие им выигрыши (табл. 7.1).
. В принципе мы можем составить прямоугольную матрицу, в которой перечислены стратегии игроков и соответствующие им выигрыши (табл. 7.1). B
А
B
А


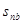
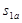

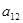


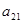
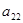
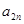
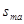
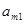

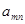
 поочерёдно для каждой своей стратегии. При использовании стратегии
поочерёдно для каждой своей стратегии. При использовании стратегии 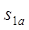 , гарантированным будет наименьшее из значений
, гарантированным будет наименьшее из значений  характеризуется показателем
характеризуется показателем 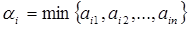
 , и наилучшей с точки зрения А является та стратегия, для которой величина
, и наилучшей с точки зрения А является та стратегия, для которой величина 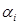 максимальна и равна a. Она называется максиминной стратегией, обеспечивающей выигрыш:
максимальна и равна a. Она называется максиминной стратегией, обеспечивающей выигрыш: 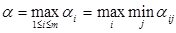 .
.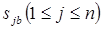 должна характеризоваться показателем
должна характеризоваться показателем 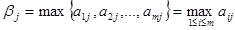 , определяющим наибольший из ожидаемых проигрышей. Очевидно лучшей стратегией становится для В, стратегия дающая минимум
, определяющим наибольший из ожидаемых проигрышей. Очевидно лучшей стратегией становится для В, стратегия дающая минимум 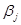 , равный b. Она называется минимаксной стратегией, так как
, равный b. Она называется минимаксной стратегией, так как  . Величина b называется верхней ценой игры или минимаксным проигрышем.
. Величина b называется верхней ценой игры или минимаксным проигрышем.


