
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Игровые модели. Графоаналитический метод решенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: Изучение теоретических и практических приёмов решения игровых моделей. Графоаналитический метод решения применим к играм вида 2 Поскольку игрок А имеет только две стратегии, то p2=1-p1 и ожидаемые выигрыши игрока А,соответствующие чистым стратегиям игрока В, представлены в таблице 7.5. Таблица 7.4. Платежная матрица игры 2 x n
Таблица 7.5. Ожидаемые выигрыши.
Отсюда видно, что ожидаемый выигрыш игрока А линейно зависит от p1. В соответствии с критерием минимакса для игр в смешанных стратегиях игрок А должен выбирать p1 так, чтобы максимизировать свой минимальный ожидаемый выигрыш. Эта задача может быть решена графически построением прямых линий, соответствующих линейным функциям от p1. Рассмотрим решение на примере (табл.7.6).
Таблица 7.6. Платежная матрица вида 2x4
Эта игра не имеет седловой точки. Ожидаемые выигрыши игрока А, соответствующие чистым стратегиям В, представлены в таблице 7.7. На рис. 7.1 изображены четыре прямые, являющиеся графиками этих функций от p1.
Таблица 7.7. Ожидаемые выигрыши.
Рис 7.1. Графическое решение игры по отношению к игроку A
Максимин достигается при p1 = ½. В этой точке пересекаются любые две из прямых 2, 3 и 4. Следовательно, оптимальной стратегией игрока А является (p1 = ½, p2 = ½) и значение игры находится подстановкой p1 в уравнение любой из прямых, проходящих через максиминную точку. Это дает ν* = 5/2. Интересно отметить, что при определении оптимальных стратегий игрока В три прямые проходят через максиминную точку. Это означает, что оптимальная стратегия В представляет собой совокупность трех стратегий. Любые две прямые, имеющие противоположные наклоны, определяют одно возможное оптимальное решение. Таким образом, из трех комбинаций (2, 3), (2, 4) и (3, 4) комбинация (2, 4) должна быть исключена как неоптимальная.
Комбинация (2, 3) дает q1=q4=0. Следовательно, q3 = 1- q2. Ожидаемые проигрыши игрока В, соответствующие чистым стратегиям А, представлены в таблице 7.8.
Таблица 7.8. Ожидаемые проигрыши
Значение q2 = ½ (соответствующее минимаксной точке) определяется из равенства –q2+3=q2+2 Отметим, что подстановкой q2 = ½ в выражение для ожидаемого проигрыша игрока В можно найти минимаксное значение, равное 5/2, совпадающее, как и должно быть, со значением игры n*. Аналогично может быть рассмотрена и комбинация (3, 4), дающая другое оптимальное решение. Любое взвешенное среднее комбинаций (2, 3) и (3, 4) также будет давать оптимальное решение, в которое входят стратегии 2, 3 и 4. Пример. Рассмотрим следующую игру вида 4x2 (табл. 7.9).
Таблица 7.9. Игра вида m x 2
Эта игра не имеет седловой точки. Пусть q1и q2(=1-q1) - смешанные стратегии игрока В. Ожидаемые проигрыши игрока B приведены в таблице 7.10. Четыре прямые из табл.7.10 изображены на рис. 7.2. Таблица 7.10. Ожидаемые проигрыши
Минимаксная точка определяется как самая нижняя точка на огибающей сверху. У\ определяет точка пересечения прямых 1 и 3, что дает q1=2/3 и n*=8/3. Прямые, пересекающиеся в минимаксной точке, соответствуют чистым стратегиям 1 и 3 игрока А. Это дает p2 = p4 = 0.Следовательно, p1 = 1- p3.
Рис. 7.2. Графическое решение игры по отношению к игроку B
Ожидаемые выигрыши игрока А, соответствующие чистым стратегиям игрока В, приведены ниже в таблице 7.11. Значение p1 = 1/3 определяется из уравнения -p1+3=2p1+2, p3=2/3, n*=8/3.
Таблица 7.11. Ожидаемые выигрыши
Варианты заданий моделей антагонистических игр приведены в таблице П.6. Найти оптимальное решение игры. Предварительно найти оценки игры и упростить игру, используя Паретовские правила отношений.
Практическая работа №8
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 818; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.73.17 (0.009 с.) |

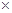 n и m
n и m  B
A
B
A





