
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретические основы решения ЗЛП (продолжение)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Как мы увидели в предыдущем пункте, при решении ЗЛП аналитическим методом имеются определённые признаки, по которым можно определить, является ли данное опорное решение оптимальным. Конечно, те признаки, которыми мы пользовались, чисто интуитивные. Мы приведём здесь научные признаки. Пусть X 1 - некоторое опорное решение ЗЛП (1.6), причём в (1.6) базисные переменные уже выражены через свободные, то есть в этой системе базисные переменные уже исключены из всех уравнений, кроме одного, в который она входит с коэффициентом 1. Например, если в X 1 базисными являются x 1, x 2, …, xn, то (1.6) имеет вид c 1 x 1+ c 2 x 2+…+ cnxn ®max(min)
Обозначим через Iб =(i 1, i 2, …, im) вектор индексов переменных, входящих в базис, а через Cб =( Величина D k = CбAk - ck = Так в ситуации (1.7) имеем D k = Пусть опорное решение X 2 получено из X 1 переводом некоторой переменной xk из свободных в базисные. Введём обозначение qk = 3.5.1. CX 2- CX 1=- qk D k. Другими словами, при переходе от опорного решения X 1 к опорному решению X 2 включением в число базисных переменных xk значение целевой функции меняется на - qk D k. Отсюда получаем, что 3.5.2. Для получения более высокого значения целевой функции (при решении задачи на максимум) необходимо включить в число базисных переменных переменную xk такую, что D k <0. Для получения более низкого значения целевой функции (при решении задачи на минимум) необходимо включить в число базисных переменных переменную xk такую, что D k >0. 3.5.3. Если в опорном решении X для всех свободных переменных xk имеет место оценка D k ≥0, то на X достигается максимум целевой функции, а если D k ≤0, то - минимум. Условия D k ≥0 для максимума и D k ≤0 для минимума называются достаточными условиями решения задачи. Если они не выполняются или для всех свободных переменных xk имеет место aik ≤0 при любом i Î Iб, то ЗЛП не имеет решений.
Симплекс-метод решения ЗЛП Алгоритм симплекс-метода Пусть имеется ЗЛП (1.6). Из предыдущего параграфа вытекает, что для нахождения решения ЗЛП достаточно последовательно перебрать угловые точки (число которых конечное) области допустимых решений задачи и выбрать ту, в которой достигается экстремум целевой функции. На этом строится симплекс-метод решения ЗЛП, алгоритм которого - следующий: 1. Привести задачу к каноническому виду. 2. С помощью метода Жордана-Гаусса найти очередное опорное решение. 3. Проверить на оптимальность очередное опорное решение. Если оно оптимальное, то задача решена. В противном случае перейти к пункту 2. Опорное решение, полученное на первом шаге, называется первоначальным опорным планом. Для нахождения первоначального опорного плана (после приведения задачи к каноническому виду) поступаем следующим образом: 1. Из векторов условий A 1, A 2, …, An включаем в базис те, которые являются стандартными единичными (то есть те, у которых все координаты нулевые, кроме одной, которая равна 1; среди них обязательно окажутся те, которые соответствуют дополнительным переменным с положительным знаком). Соответствующие переменные будут включены в базис. Если число таких векторов условий равно m, то первоначальный опорный план построен: им является решение системы ограничений, полученное приравниванием свободных переменных к 0. В противном случае идём к пункту 2. 2. Допустим, переменная xk пока не вошла в базис. Тогда выбираем уравнение, в котором отношение Если во всех уравнениях коэффициент при xk будет неположительным (то есть aik £0), то xk нельзя включать в базис. Кроме того, если минимум чисел Пример 1. Найти первоначальный опорный план задачи: -3 x 1+ x 2+2 x 3®max(min)
Решение. Решим задачу вначале «вручную». 1. Приведём задачу к каноническому виду. Для этого сначала умножим второе неравенство системы ограничений на (-1) (добиваемся, чтобы правые части всех нетривиальных ограничений имели знак «+»). Получаем систему ограничений
Теперь добавляем во второе и третье неравенства системы дополнительные переменные x 4 и x 5:
Таким образом, получаем канонический вид исходной задачи: -3 x 1+ x 2+2 x 3®max(min)
2. С помощью метода Жордана-Гаусса найдём первоначальный опорный план. Прежде всего замечаем, что дополнительная переменная x 4 входит только во второе уравнение. И она уже в базисе. Так как для x 2 min
Две базисные переменные из первого и второго уравнений выбраны. Осталось выбрать третью базисную переменную из третьего уравнения. Переменные x 3 и x 5 для этого не годятся, так как коэффициенты при них отрицательны. Остаётся только x 1. Для того, чтобы её ввести в базис необходимо, чтобы минимум отношений свободных членов к положительным коэффициентам достигался в третьем уравнении. Так оно и есть: min
Таким образом, при x 3=0, x 5=0 имеем x 1=2, x 2=4, x 4=2 и X 1=(2; 4; 0; 2; 0) - первоначальный опорный план. Ответ: X 1=(2; 4; 0; 2; 0) - первоначальный опорный план. Проверка опорного плана на оптимальность проводится по следующей схеме: 1. Находятся оценки D k = CбAk - ck = 2. Если условие оптимальности опорного плана выполнено (D k ³0 для всех k =1, …, n при поиске максимума, D k £0 для всех k =1, …, n при поиске минимума), то задача решена. В противном случае переходят к другому опорному плану. Переход к другому опорному плану проводится по следующей схеме: 1. Для всех D k, для которых нарушается условие оптимальности задачи, вычисляются qk = 2. Выбирается xk такой, что |- qk D k | является максимальным. Эту xk и вводим в базис, выводя из него xi, в которой достигается минимальное qk, по методу Жордана-Гаусса. Пример 2. Решить задачу предыдущего примера (найти экстремумы). Решение. При решении предыдущего примера канонический вид задачи и её первоначальный опорный план найдены. Проверим на оптимальность решение X 1. Для этого необходимо вычислить D k = CбAk - ck для k - индексов свободных переменных. При k =3 имеем D3= CбA 3- c 3=(1, 0, -3)× то есть D3=1≥0. В частности, в X 1 минимум не достигается. D5= CбA 5- c 5=(1, 0, -3)× то есть D5=1≥0. Так как D k ≥0 для всех k =1, 2, 3, 4, 5, то в X 1 достигается максимум целевой функции, который равен D0= CX =-3×2+4+2×0=-2. Минимум в этой точке не достигается. Перейдём к другому опорному плану. Для D3 и D5, для которых нарушается условие оптимальности, вычислим q 3 и q 5, а по ним - величины - q 3D3 и - q 5D5: q 3= - q 3D3=- q 5= - q 5D5=-4×1=-4. Так как |- q 5D5|=|-4|>|-
Получили новый опорный план X 2=(4; 6; 0; 0; 4), который проверяем на оптимальность: D3= CбA 3- c 3=(1, 0, -3)× D4= CбA 4- c 4=(1, 0, -3)× Таким образом, D3=-2<0, D4=-2<0, то есть D k ≤0 для всех k =1, 2, 3, 4, 5. Значит, X 2 - оптимальное решение задачи с точки зрения минимизации. В нём CX =-3×4+6+2×0=-6. Ответ: F min=-6, минимум достигается в точке X 2=(4; 6; 0); F max=-2, максимум достигается в точке X 1=(2; 4; 0).
Симплекс-таблицы. Все вычисления в симплекс-методе принято производить в таблицах. Прежде всего, в отдельных таблицах вида
производятся преобразования Жордана-Гаусса. Затем составляется симплекс-таблица вида
в которой D k =0 сразу проставляются для всех базисных векторов условий и D k = CбAk - ck для небазисных, столбцы qk вычисляются только для свободных переменных xk, наконец, для тех из них, для которых не выполнено условие оптимальности, вычисляются - qk D k, и из них выбирается наибольший по абсолютной величине. Тот xk, для которого достигается этот максимум, вводится в базис. Продемонстрируем применение таблиц при решении нашего предыдущего примера. I этап. Нахождение первоначального опорного плана:
Напоминаем, что в базис включаем x 2. Имеем, что минимум min В Табл.3 в базис включаем x 1. Имеем min II этап. Применение симплекс-метода.
Комментарии опустим, предложив читателю восстановить применение метода к таблицам. 4.3. Упражнение. Решить задачи линейного программирования Упражнения 1.3 симплекс-методом.
Метод искусственного базиса
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 556; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.013 с.) |

 (1.7)
(1.7) ,
,  , …,
, …,  ) - вектор коэффициентов целевой функции при базисных переменных. Например, если мы имеем ситуацию (1.7), то Iб =(1, 2, …, m), Cб =(c 1, c 2, …, cm).
) - вектор коэффициентов целевой функции при базисных переменных. Например, если мы имеем ситуацию (1.7), то Iб =(1, 2, …, m), Cб =(c 1, c 2, …, cm). - ck называется оценкой разложения вектора условий Ak по базису опорного решения.
- ck называется оценкой разложения вектора условий Ak по базису опорного решения. - ck. Ясно, что если k Î Iб (то есть если переменная xk - базисная), то D k =0.
- ck. Ясно, что если k Î Iб (то есть если переменная xk - базисная), то D k =0. Можно доказать, что тогда
Можно доказать, что тогда (где aik >0) будет минимальным. Это (i -е) уравнение будет ведущим: разделив его на коэффициент aik при xk, добиваемся, чтобы коэффициент при xk стал равным 1, а из остальных уравнений xk исключаем (применяем метод Жордана-Гаусса). Процесс продолжаем до тех пор, пока базис не будет содержать m переменных.
(где aik >0) будет минимальным. Это (i -е) уравнение будет ведущим: разделив его на коэффициент aik при xk, добиваемся, чтобы коэффициент при xk стал равным 1, а из остальных уравнений xk исключаем (применяем метод Жордана-Гаусса). Процесс продолжаем до тех пор, пока базис не будет содержать m переменных.

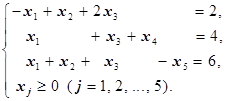
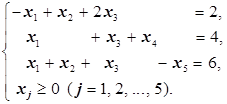
 =2 достигается в первом уравнении (при определении этого min второе уравнение не участвует, так как коэффициент при x 2 в нём равен 0), то x 2 включаем в базис, исключив его из третьего уравнения (для этого первое уравнение вычитаем из третьего):
=2 достигается в первом уравнении (при определении этого min второе уравнение не участвует, так как коэффициент при x 2 в нём равен 0), то x 2 включаем в базис, исключив его из третьего уравнения (для этого первое уравнение вычитаем из третьего):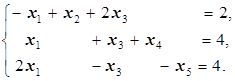
 =2 достигается в третьем уравнении. Поэтому третье уравнение делим на 2, затем прибавляем его к первому и вычитаем из второго:
=2 достигается в третьем уравнении. Поэтому третье уравнение делим на 2, затем прибавляем его к первому и вычитаем из второго:
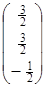 -2=1×
-2=1×  +0×
+0×  -2=1,
-2=1, -0=1×
-0=1× 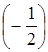 +0×
+0×  +(-3)×
+(-3)×  =
= 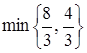 =
=  (достигается при x 4),
(достигается при x 4), =
=  =4, (достигается снова при x 4, то есть в любом случае x 4 будем выводить из базиса),
=4, (достигается снова при x 4, то есть в любом случае x 4 будем выводить из базиса),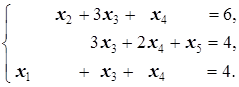
 -2=1×3+0×3+(-3)×1-2=-2,
-2=1×3+0×3+(-3)×1-2=-2, -0=1×1+0×2+(-3)×1-0=-2.
-0=1×1+0×2+(-3)×1-0=-2.


 =2 в третьей строке. Третью строку Табл.2 делим на 2 - получаем третью строку Табл.3. Затем третью строку прибавляем к первой строке и вычитаем из второй строки Табл.2. Получаем первую и вторую строки Табл.3.
=2 в третьей строке. Третью строку Табл.2 делим на 2 - получаем третью строку Табл.3. Затем третью строку прибавляем к первой строке и вычитаем из второй строки Табл.2. Получаем первую и вторую строки Табл.3.


