
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая интерпретация ЗЛПСодержание книги
Поиск на нашем сайте
Приведём геометрическую интерпретацию ЗЛП. Пусть дана ЗЛП от двух переменных: c 1 x 1+ c 2 x 2 ® max
Из 3.1.1 и 3.1.2 получаем 3.2.1. Область допустимых решений ЗЛП (3.1) является выпуклым многоугольником (возможно, бесконечным) в R 2 с конечным числом вершин. 3.2.2. Целевая функция ЗЛП (3.1) достигает экстремума в вершине многоугольника допустимых решений. При этом, если целевая функция достигает экстремума в двух вершинах многоугольника решений, то она также достигает экстремума на всей стороне (в любой точке стороны) с концами в этих вершинах. Наконец, из 3.3.1 вводной Главы 0 получаем 3.2.3. При перемещении линий уровня c 1 x 1+ c 2 x 2= a относительно начала координат в направлении вектора нормали Действительно, при перемещении линий уровня c 1 x 1+ c 2 x 2= a относительно начала координат в направлении вектора нормали На фактах 3.2.1 - 3.2.3 основывается геометрический метод решения задачи (3.1), который заключается в следующем: 1. Построить область (многоугольник) допустимых решений ЗЛП (3.1). 2. Найти крайние положения прямых уровня c 1 x 1+ c 2 x 2= a относительно ОДР. Эти положения будут либо в угловой точке (вершине), либо на стороне ОДР (многоугольника), либо таких точек не существует. 3. По направлению вектора нормали Пример. Решить геометрически ЗЛП: 4 x 1+ x 2 ® max
Решение. 1. Построим область допустимых решений задачи. Для этого построим полуплоскости, определяемые неравенствами системы ограничений. В свою очередь, для построения полуплоскости, определяемой неравенством a 1 x 1+ a 2 x 2≤ b, достаточно построить границу полуплоскости - прямую a 1 x 1+ a 2 x 2= b, и определить, которая из двух полуплоскостей относительно этой прямой является искомой. Для этого подставляем координаты какой-нибудь точки, не лежащей на прямой a 1 x 1+ a 2 x 2= b, в интересующее нас неравенство. Если получается верное числовое неравенство, то та сторона от прямой, в которой лежит точка, является искомой полуплоскостью. Построим полуплоскость 2 x 1+3 x 2≤24. Прямая 2 x 1+3 x 2=24 пересекает оси Ox 1 и Ox 2 в точках (0, 8) и (12, 0). Подставим координаты начала координат в неравенство: 2×0+3×0≤24. Так как получилось верное неравенство, то начало координат лежит в искомой полуплоскости. Это означает, что та сторона относительно прямой, в которой лежит начало координат О, является полуплоскостью 2 x 1+3 x 2≤24. Цифрами в скобках нумеруем границы полуплоскостей в
Строим полуплоскость -8 x 1+3 x 2≤24. Точки (0, 8), (-3, 0) - точки пересечения границы полуплоскости -8 x 1+3 x 2≤24 с осями координат. Далее, -8×0+3×0≤24 - верное числовое неравенство. Значит, искомая полуплоскость - та, в которой лежит начало координат (Рис. 2). Наконец, (0, -4), (6, 0) - точки пересечения прямой 2 x 1-3 x 2≤12 с осями координат, 2×0-3×0≤12. Четырёхугольник OABC - ОДР задач. (Рис. 3). 2. Найдём крайние положения прямых уровня 4 x 1+ x 2= a относительно ОДР. Эти прямые перпендикулярны вектору
f min= f (0, 0)=0, f max=4×9+2=38. Ответ: При x 1= x 2=0 достигается минимум целевой функции, равной 0; при x 1=9, x 1=2 достигается максимум, равный 38. 3.3. Упражнение. Задания 2) и 3) Упражнения 1.3 решить геометрическим методом.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 453; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.71.13 (0.006 с.) |

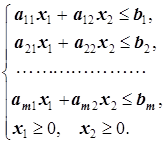 (3.1)
(3.1) =(c 1, c 2) этих (прямых) линий значение a возрастает, в противоположном направлении a убывает.
=(c 1, c 2) этих (прямых) линий значение a возрастает, в противоположном направлении a убывает.
 в порядке их следования в системе ограничений (Рис.1).
в порядке их следования в системе ограничений (Рис.1). Координаты B находим как координаты точки пересечения прямых (1) и (3), составив и решив систему из их уравнений:
Координаты B находим как координаты точки пересечения прямых (1) и (3), составив и решив систему из их уравнений: Û
Û 



