
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типичные злп и их математические моделиСодержание книги
Поиск на нашем сайте
1. Задача об использовании сырья. Некоторое производство выпускает n видов продукции с использованием m видов сырья. Известны: aij - количество i -го вида сырья, затрачиваемого на выпуск единицы продукции j -го вида; bi - запасы i -го вида сырья; cj - прибыль от реализации единицы продукции j -го вида. Составить план производства продукции (то есть определить, в каком количестве выпустить каждого вида продукции), обеспечивающий максимальную прибыль. Составим математическую модель задачи. Обозначим через xj количество выпускаемой продукции j -го вида; x 1 - количество выпускаемой продукции 1-го вида, x 2 - количество выпускаемой продукции 2-го вида и т.д. Тогда c 1 x 1 - прибыль от реализации всей произведённой продукции 1-го вида, и, вообще, cjxj - прибыль от реализации всей произведённой продукции j -го вида, c 1 x 1+ c 2 x 2+…+ cnxn - общая прибыль от реализации всей произведённой продукции. Это - целевая функция, максимум которой мы должны получить: c 1 x 1+ c 2 x 2+…+ cnxn ®max. Количество сырья первого вида, затрачиваемого на выпуск единицы продукции первого вида, равно a 11, x 1 - количество выпускаемой продукции первого вида. Поэтому всего сырья первого вида на выпуск всей продукции первого вида уйдёт в количестве a 11 x 1. Аналогично, a 12 x 2 - общее количество сырья первого вида, которое уйдёт на впуск всей продукции второго вида и т.д. Всего же количество сырья первого вида, которое уйдёт на производство всех видов продукции, равно a 11 x 1+ a 12 x 2+…+ a 1 nxn, и оно не может превосходить общие запасы сырья первого вида, то есть b 1: a 11 x 1+ a 12 x 2+…+ a 1 nxn ≤ b 1. Аналогично рассуждая в общем случае относительно i -го вида сырья, получим неравенство ai 1 x 1+ ai 2 x 2+…+ ainxn ≤ bi (i =1, 2, …, m). Наконец, количество выпускаемой продукции j -го вида не может быть отрицательным: xj ≥0 (j =1, 2, …, n). И мы приходим к следующей математической модели задачи: c 1 x 1+ c 2 x 2+…+ cnxn ®max
2. Задача о составлении рациона (задача о диете). Сельхозпредприятие занимается откормом скота. В откормочный рацион входит n видов продуктов, которые содержат m видов питательных веществ. Известны: aij - количество i -го вида питательного вещества в единице продукта j -го вида; bi - необходимое количество питательного вещества i -го вида, содержащегося в рационе; cj - стоимость единицы продукта j -го вида. Составить рацион (то есть определить, в каком количестве включить в рацион продукта каждого вида), при котором достигается минимальная стоимость рациона. Составим математическую модель задачи. Обозначим через xj количество продуктов j -го вида, включаемого в рацион. Тогда c 1 x 1+ c 2 x 2+…+ cnxn - общая стоимость рациона, которая должна быть минимальной: c 1 x 1+ c 2 x 2+…+ cnxn ®min. Количество питательного вещества первого вида, входящего в единицу продукта первого вида, равно a 11, x 1 - количество продукта первого вида, входящего в рацион. Поэтому всего питательного вещества первого вида, входящего в рацион с продуктами первого вида, составит a 11 x 1. Аналогично, a 12 x 2 - общее количество питательного вещества второго вида, входящего в рацион с продуктами второго вида, и т.д. Всего же количество питательного вещества первого вида, которое поступит в рацион со всеми видами продуктов, равно a 11 x 1+ a 12 x 2+…+ a 1 nxn, и оно не может быть меньше положенного количества, то есть b 1: a 11 x 1+ a 12 x 2+…+ a 1 nxn ≥ b 1. Аналогично рассуждая в общем случае относительно i -го вида питательных веществ, получим неравенство ai 1 x 1+ ai 2 x 2+…+ ainxn ≥ bi (i =1, 2, …, m). Наконец, количество продуктов, входящих в рацион, не может быть отрицательным: xj ≥0 (j =1, 2, …, n). И мы приходим к следующей математической модели задачи: c 1 x 1+ c 2 x 2+…+ cnxn ®min
Упражнения. 1) Какие из следующих задач являются задачами линейного программирования, какие нет: а) -2 x 1+ x 2+8 x 3-2 x 4®min б) -2 x 1+
в) -3 x 1-2 x 2+ x 3®min(max) г) 4 x 1+ x 2®min(max)
д) -3 x 1-2 x 2+ x 3®min(max) е) 4 x 1+ x 2®min(max)
ж) -3 x 1+ x 2+2 x 3®max(min) з) -3 x 1+2 x 2+2 x 3®max(min)
Решение. а) задача является задачей линейного программирования, так как и целевая функция -2 x 1+ x 2+8 x 3-2 x 4, и функции б) Задача не является задачей линейного программирования, так как целевая функция не является линейной - переменная x 2 входит в функцию в квадрате: Составить математические модели следующих задач: 2) При производстве двух видов продукции используется три вида сырья. Составить план выпуска продукции, обеспечивающий максимум прибыли. Исходные данные приводятся в таблицах:
3) В рационе животных используется два вида кормов. Животные должны получать три вида питательных веществ. Составить рацион наименьшей стоимости. Исходные данные приводятся в таблицах:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 438; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.006 с.) |

 (1.4)
(1.4) (1.5)
(1.5) +8 x 3-2 x 4®min
+8 x 3-2 x 4®min





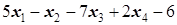 и
и  в ограничениях линейные.
в ограничениях линейные.


