Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пара несимметричных двойственных задачСодержание книги
Поиск на нашем сайте
Пара двойственных задач может также быть несимметричной. Несимметричная пара двойственных задач удовлетворяет следующим условиям: 1. Матрицы систем ограничений задач транспонированы по отношению к друг другу. 2. Каждому ограничению одной задачи соответствует переменная во второй задаче; при этом переменная, соответствующая ограничению-неравенству в одной задаче, удовлетворяет условию неотрицательности в другой, а переменная, соответствующая ограничению-равенству, может быть любого знака. 3. Коэффициенты при переменных в целевой функции одной задачи являются свободными членами соответствующих ограничений другой. При этом свободные члены целевых функций задач совпадают. 4. Целевые функции задач оптимизируются противоположным образом, то есть если одна из задач - на максимум, то вторая - на минимум, а если одна из задач на минимум, то вторая - на максимум. 5. Если целевая функция задачи максимизируется, то знаки неравенств в ограничениях задачи имеют вид «£», а если минимизируется, то имеют вид «³». 6. Во всех ограничениях задач свободные члены находятся в правой части, а члены с переменными - в левой. Наконец, условия 1 - 6 называются условиями двойственности. Таким образом, симметричная и несимметричная пары двойственных задач отличаются только 2-м условием. Пример 1. Составить двойственные к задачам: а) 2 x 1+2 x 2-5 x 3 ® max(min); б) 2 x 1+2 x 2-5 x 3 ® min
Решение. а) Сначала составим двойственную к задаче на максимум (max). Двойственная - следующая: 12 y 1-2 y 2+24 y 3 ® min
Покажем, что действительно получили двойственную задачу. Для этого покажем, что для пары 2 x 1+2 x 2-5 x 3 ® max 12 y 1-2 y 2+24 y 3 ® min
задач выполнены все условия двойственности. 1. Матрицы систем ограничений задач транспонированы по отношению к друг другу:
2. В каждой задаче по три ограничения и три переменные, то есть каждому ограничению одной задачи соответствует переменная в другой задаче. При этом все переменные одной задачи соответствуют ограничениям-неравенствам другой, и поэтому удовлетворяют условиям неотрицательности. 3. Коэффициенты 2, 2, -5 при переменных в целевой функции первой задачи являются свободными членами соответствующих ограничений второй и, наоборот, коэффициенты 12, -2, 24 при переменных в целевой функции второй задачи являются свободными членами соответствующих ограничений первой. При этом свободные члены целевых функций задач совпадают (оба равны 0). 4. Целевые функции задач оптимизируются противоположным образом: исходная задача - на максимум, а вторая - на минимум. 5. Выдержаны требования к соответствию типа экстремума целевой функции к типам неравенств в ограничениях: если целевая функция задачи максимизируется, то знаки неравенств в ограничениях задачи имеют вид «£», а если минимизируется, то имеют вид «³». Теперь составим двойственную к задаче на минимум (min). Тогда исходную необходимо переписать согласно виду экстремума целевой функции - минимума. Это означает, что все нетривиальные неравенства в исходной задаче должны принять вид «³». Для этого достаточно эти неравенства умножить на -1: а) 2 x 1+2 x 2-5 x 3 ® min
Двойственная - следующая: -12 y 1+2 y 2-24 y 3 ® max
Убеждаемся в этом точно так же, как и в предыдущем случае. б) Двойственная - следующая: 12 y 1-2 y 2+24 y 3 ® max
Покажем, что действительно получили двойственную задачу. Для этого покажем, что для пары 2 x 1+2 x 2-5 x 3 ® min 12 y 1-2 y 2+24 y 3 ® max
задач выполнены все условия двойственности. 1. Матрицы систем ограничений задач транспонированы по отношению к друг другу:
2. В каждой задаче по три ограничения и три переменные, то есть каждому ограничению одной задачи соответствует переменная в другой задаче. При этом переменные x 1, x 2, x 3, y 1, y 2, соответствующие ограничениям-неравенствам в одной задаче, удовлетворяет условиям неотрицательности в другой, а переменная y 3, соответствующая ограничению-равенству в первой, может быть любого знака (на неё ограничение неотрицательности не накладывается). 3. Коэффициенты 2, 2, -5 при переменных в целевой функции первой задачи являются свободными членами соответствующих ограничений второй и, наоборот, коэффициенты 12, -2, 24 при переменных в целевой функции второй задачи являются свободными членами соответствующих ограничений первой. При этом свободные члены целевых функций задач совпадают (оба равны 0). 4. Целевые функции задач оптимизируются противоположным образом: исходная задача - на минимум, а вторая - на максимум. 5. Выдержаны требования к соответствию типа экстремума целевой функции к типам неравенств в ограничениях: если целевая функция задачи максимизируется, то знаки неравенств в ограничениях задачи имеют вид «£», а если минимизируется, то имеют вид «³». Во всех ограничениях задач свободные члены находятся в правой части, а члены с переменными - в левой. Теоремы двойственности 1.4.1. Теорема (первая теорема двойственности). Значения целевых функций пары двойственных задач на их оптимальных планах совпадают. 1.4.2. Теорема (вторая теорема двойственности). Пусть X 0=(
В силу данной теоремы для решения пары двойственных задач (1.1) и (1.2) достаточно поступить следующим образом: сначала решить одну из них, например (1.1), и по её решению X 0=( Теоремы эти справедливы также и для пары несимметричных двойственных задач. Так что они также применимы и при нахождении решения одной из двух несимметричных двойственных задач при условии, что решение другой известно. Пример 2. Составить двойственную и по решению исходной найти её решение: 2 x 1+2 x 2-5 x 3®min
Решение. Двойственная - следующая: 12 y 1-2 y 2+24 y 3 ® max
(См. Пример 1б)). Находим решение исходной симлекс-методом или методом искусственного базиса. Решение возможно и на компьютере, например, в оболочке Excel: X 0=(0, 28, 26), F min=-74 - решение исходной задачи. Составим систему (1.3) для нашей задачи (и решим её), которая в случае n = m =3 имеет вид:
Из третьего уравнения последней системы получаем
Решим эту систему, например, правилом Крамера. Как известно, согласно правила Крамера Ответ: Двойственная и её решение: 12 y 1-2 y 2+24 y 3 ® max
Y 0=(0, 1, -3), Упражнения. 1) По решению исходной найти решение двойственной к задачам из Примера 1а). 2) Составить двойственные и по решениям исходных найти их решения для ЗЛП из Упражнения 1.3 Главы I.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.17.137 (0.009 с.) |




 =
=  .
.

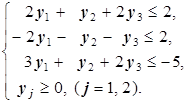

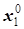 ,
, 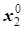 , …,
, …, 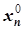 ) и Y 0=(
) и Y 0=( ,
,  , …,
, …,  ) - решения соответственно задач (1.1) и (1.2). Тогда они связаны соотношениями
) - решения соответственно задач (1.1) и (1.2). Тогда они связаны соотношениями (1.3)
(1.3)
 Û
Û Û
Û 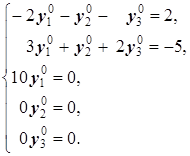
 , подставляя которое в первые два, приходим к системе
, подставляя которое в первые два, приходим к системе
 =
=  ,
,  =
=  где D - определитель системы, D1 и D2 - определители, полученные из D заменой на столбец свободных членов соответсвенно первого и второго столбцов. Имеем D=
где D - определитель системы, D1 и D2 - определители, полученные из D заменой на столбец свободных членов соответсвенно первого и второго столбцов. Имеем D=  =-1, D1=
=-1, D1= 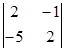 =-1, D2=
=-1, D2=  =3. Поэтому
=3. Поэтому  =1,
=1,  =-3. Окончательно имеем Y 0=(0, 1, -3),
=-3. Окончательно имеем Y 0=(0, 1, -3),  =-74.
=-74.