
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приводим задачу к каноническому виду.Содержание книги
Поиск на нашем сайте
Если в системе ограничений задачи присутствуют только уравнения, а свободные члены в системе ограничений задачи являются неотрицательными, то говорят, что задача имеет канонический вид. Любая смешанная система приводится к системе уравнений добавлением дополнительных неотрицательных переменных со знаком «+» в неравенства типа «≤» и со знаком «-» в неравенства типа «≥». Поэтому для приведения к каноническому виду задачи линейного программирования поступаем следующим образом: 1) Если в системе ограничений задачи имеется ограничение с отрицательной правой частью, то умножаем его на -1. 2) Добавляем в каждое неравенство дополнительные неотрицательные переменные: со знаком «+» в неравенства типа «≤» и со знаком «-» в неравенства типа «≥». Применительно к нашей системе: сначала умножим второе неравенство системы ограничений на (-1) (добиваемся, чтобы правые части всех нетривиальных ограничений имели знак «+»). Получаем систему ограничений
Теперь добавляем во второе и третье неравенства системы дополнительные переменные x 4 и x 5:
Таким образом, получаем канонический вид исходной задачи: -3 x 1+ x 2+2 x 3®max(min)
2. С помощью метода Жордана-Гаусса находим очередное опорное решение. Самое первое опорное решение носит название первоначального опорного плана. Для нахождения первоначального опорного плана (после приведения задачи к каноническому виду) поступаем следующим образом: 3. Из векторов условий A 1, A 2, …, An включаем в базис те, которые являются стандартными единичными (то есть те, у которых все координаты нулевые, кроме одной, которая равна 1; среди них обязательно окажутся те, которые соответствуют дополнительным переменным с положительным знаком). Соответствующие переменные будут включены в базис. Если число таких векторов условий равно m, то первоначальный опорный план построен: им является решение системы ограничений, полученное приравниванием свободных переменных к 0. В противном случае идём к пункту 2. 4. Допустим, переменная xk пока не вошла в базис. Тогда выбираем уравнение, в котором отношение
Если во всех уравнениях коэффициент при xk будет неположительным (то есть aik £0), то xk нельзя включать в базис. Кроме того, если минимум чисел Применительно к нашей задаче прежде всего замечаем, что дополнительная переменная x 4 входит только во второе уравнение. И она уже в базисе. Так как для x 2 min
Две базисные переменные из первого и второго уравнений выбраны. Осталось выбрать третью базисную переменную из третьего уравнения. Переменные x 3 и x 5 для этого не годятся, так как коэффициенты при них отрицательны. Остаётся только x 1. Для того, чтобы её ввести в базис необходимо, чтобы минимум отношений свободных членов к положительным коэффициентам достигался в третьем уравнении. Так оно и есть: min
Таким образом, при x 3=0, x 5=0 имеем x 1=2, x 2=4, x 4=2 и X 1=(2; 4; 0; 2; 0) - первоначальный опорный план. 3. Проверим на оптимальность очередное опорное решение. Если оно оптимальное, то задача решена. В противном случае перейдём к пункту 2. Проверка опорного плана на оптимальность проводится по следующей схеме: 3. Находятся оценки D k = CбAk - ck = 4. Если условие оптимальности опорного плана выполнено (D k ³0 для всех k =1, …, n при поиске максимума, D k £0 для всех k =1, …, n при поиске минимума), то задача решена. В противном случае переходят к другому опорному плану.
Данные вычислений принято вносить в так называемые симплекс таблицы вида
В нашем примере мы можем заполнить эту таблицу с учётом (*):
Итак, для проверки оптимальности опорного плана вычисляем D k = CбAk - ck для k - индексов свободных переменных, заполняя соответствующие клетки таблицы:
Приведём сами вычисления: имеем D3= CбA 3- c 3=(1, 0, -3)× то есть D3=1≥0. В частности, в X 1 минимум не достигается. D5= CбA 5- c 5=(1, 0, -3)× то есть D5=1≥0. Так как D k ≥0 для всех k =1, 2, 3, 4, 5, то в X 1 достигается максимум целевой функции, который равен D0= CX =-3×2+4+2×0=-2. Минимум в этой точке не достигается. Значит, необходимо перейти к другому опорному плану. Переход к другому опорному плану проводится по следующей схеме: 3. Для всех D k, для которых нарушается условие оптимальности задачи, вычисляются qk = 4. Выбирается xk такой, что |- qk D k | является максимальным. Эту xk и вводим в базис, выводя из него xi, в которой достигается минимальное qk, по методу Жордана-Гаусса. В нашем примере для D3 и D5, для которых нарушается условие оптимальности, вычислим q 3 и q 5, а по ним - величины - q 3D3 и - q 5D5: q 3= - q 3D3=- q 5= - q 5D5=-4×1=-4. Наша таблица окончательно принимает вид
Так как |- q 5D5|=|-4|>|-
Получили новый опорный план X 2=(4; 6; 0; 0; 4). Находим для неё оценки D k для всех k =1, 2, 3, 4, 5:
Таким образом, D3=-2<0, D4=-2<0, то есть D k ≤0 для всех k =1, 2, 3, 4, 5. Значит, X 2 - оптимальное решение задачи с точки зрения минимизации. В нём CX =-3×4+6+2×0=-6. 1б) Метод искусственного базиса заключается в том, что симплекс-метод применяется к так называемой вспомогательной задаче. Пусть задача приведена к каноническому виду, в котором в некоторых уравнениях, скажем в i 1-м, i 2-м, …, is -м, явно не выделяются базисные переменные. Добавим в эти уравнения искусственные переменныеxm +1, xm +2, …, xm + s, а в целевую функцию - слагаемые ± Mxm +1, ± Mxm +2, …, ± Mxm + s, где M >>1 (M - достаточно большое положительное число) причём «±» - это «+», если решается задача на min, и «±» - это «-», если решается задача на max. Получается новая задача, которая называется дополнительной или вспомогательной. Алгоритм метода - следующий: 4. Привести задачу к каноническому виду. 5. Если в задаче в каноническом виде нет базиса из единичных векторов, то составить вспомогательную задачу (если в задаче в каноническом виде имеется базис из единичных векторов, то задача решается обычным симплекс-методом). 6. Решить вспомогательную задачу, и если ( При этом к вспомогательной задаче применяется обычный симплекс-метод с некоторыми своими особенностями: 4. Так как целевая функция вспомогательной задачи имеет слагаемые с коэффициентами ± M, то оценки D k имеют вид 5. Искусственные переменные по мере их выведения из базиса исключаются из дальнейшего рассмотрения. 6. После того, как все искусственные переменные будут выведены из базиса, коэффициенты D k при M будут равны нулю, в таблице остаётся только строка Применяем к нашей задаче описанный алгоритм: 1. Приведём задачу к каноническому виду:
-3 x 1+ x 2+2 x 3 ® max(min)
2. В базис в виде единичного вектора входит только вектор при x 4, то есть переменная во втором уравнении. В первое и третье уравнения системы ограничений вводим искусственные переменные x 6 и x 7:
В целевую функцию они войдут с коэффициентами M или - M в зависимости от того, решается задача на min или на max. Решим задачу на максимум. Тогда вспомогательная задача - следующая: -3 x 1+ x 2+2 x 3- Mx 6- Mx 7 ® max
3. Решаем полученную вспомогательную задачу с применением симплекс-таблиц:
Здесь D2=-2 M -1, D3=-3 M -2. Коэффициенты при M записаны в строке
Так как D k <0 только для одного значения k =1, а именно, D1=-2 M +2<0 (напоминаем, что M - достаточно большое число, так что -2 M <2 и D1<0), то ищем только отношения q 1. Минимум этих отношений достигается в строке x 7: min Искусственные переменные теперь исключены из базиса. Поэтому дальше работаем с обычной симплекс-таблицей, в которой новая третья строка (соответствующая переменной x 1) получается делением старой третьей строки на 2. Затем эту новую третью прибавляем к старой первой и вычитаем из старой второй. В результате в новой таблице в столбце x 1 появятся соответственно 0, 0 и 1:
В полученной таблице D k ³0 для всех k =1, 2, …, 5, то есть критерий оптимальности выполнен. Поэтому X 0=(2; 4; 0) является оптимальным решением, при котором значение целевой функции равно -2 (x 4 в окончательном ответе не учитывается, так как она является дополнительной переменной, и не входит в первоначальную задачу). Решим задачу на минимум (min). Тогда вспомогательная задача - следующая: -3 x 1+ x 2+2 x 3- Mx 6- Mx 7 ® max
Как и выше, решаем полученную вспомогательную задачу с применением симплекс-таблицы:
Критерий оптимальности нарушается для переменных x 2 и x 3: D2=2 M -1>0, D3=3 M -2>0. Так как - q 2D2=-4 M +2 по абсолютной величине превосходит - q 3D3=-3 M +2, то в базис включаем x 2. При этом min
Теперь D1>0. Поэтому переход к новой таблице аналогичен соответствующему переходу при решении задачи на max: в базис вводится x 1 вместо x 7:
Имеем D3=1>0 и D5=1>0. Так как |- q 5D5|=|- q 3D3|, то вводим в базис x 5 (вместо x 4): сначала умножаем 2-ю строку на 2, а затем новую вторую строку, умноженную на ½, прибавляем к первой и третьей (фактически вторую старую прибавляем к первой и третьей):
В полученной таблице D k £0 для всех k =1, 2, …, 5, то есть критерий оптимальности выполнен. Поэтому X 0=(4; 6; 0) является оптимальным решением, при котором значение целевой функции равно -6. 2) Несимметричная пара двойственных задач удовлетворяет следующим условиям: 1. Матрицы систем ограничений задач транспонированы по отношению к друг другу. 2. Каждому ограничению одной задачи соответствует переменная во второй задаче; при этом переменная, соответствующая ограничению-неравенству в одной задаче, удовлетворяет условию неотрицательности в другой, а переменная, соответствующая ограничению-равенству, может быть любого знака. 3. Коэффициенты при переменных в целевой функции одной задачи являются свободными членами соответствующих ограничений другой. При этом свободные члены целевых функций задач совпадают. 4. Целевые функции задач оптимизируются противоположным образом, то есть если одна из задач - на максимум, то вторая - на минимум, а если одна из задач на минимум, то вторая - на максимум. 5. Если целевая функция задачи максимизируется, то знаки неравенств в ограничениях задачи имеют вид «£», а если минимизируется, то имеют вид «³». 6. Во всех ограничениях задач свободные члены находятся в правой части, а члены с переменными - в левой. Условия 1 - 6 называются условиями двойственности. Применительно к нашей задаче сначала составим двойственную к задаче на max: -3 x 1+ x 2+2 x 3 ® max
Согласно условию 5 для пары несимметричных двойственных задач, если целевая функция задачи максимизируется, то знаки неравенств в ограничениях задачи имеют вид «£». Поэтому умножаем второе и третье неравенства системы ограничений на -1: -3 x 1+ x 2+2 x 3 ® max
Двойственная - следующая: 2 y 1+4 y 2-6 y 3 ® min
Покажем, что действительно получили двойственную задачу. Для этого покажем, что для пары -3 x 1+ x 2+2 x 3 ® max 2 y 1+4 y 2-6 y 3 ® min
задач выполнены все условия двойственности. 1. Матрицы систем ограничений задач транспонированы по отношению к друг другу:
2. В каждой задаче по три ограничения и три переменные, то есть каждому ограничению одной задачи соответствует переменная в другой задаче. При этом все вторая и третья переменные второй задачи соответствуют второму и третьему ограничениям-неравенствам первой, и поэтому удовлетворяют условиям неотрицательности. Наоборот, все переменные первой задачи удовлетворяют условиям неотрицательности, и поэтому все ограничения второй имеют тип неравенств. 3. Коэффициенты -3, 1, 2 при переменных в целевой функции первой задачи являются свободными членами соответствующих ограничений второй и, наоборот, коэффициенты 2, 4, -6 при переменных в целевой функции второй задачи являются свободными членами соответствующих ограничений первой. При этом свободные члены целевых функций задач совпадают (оба равны 0). 4. Целевые функции задач оптимизируются противоположным образом: исходная задача - на максимум, а вторая - на минимум. 5. Выдержаны требования к соответствию типа экстремума целевой функции к типам неравенств в ограничениях: если целевая функция задачи максимизируется, то знаки неравенств в ограничениях задачи имеют вид «£», а если минимизируется, то имеют вид «³». Теперь составим двойственную к задаче на минимум (min): -3 x 1+ x 2+2 x 3 ® min
Условие 5 для исходной задачи выдержано: если целевая функция задачи минимизируется, то знаки неравенств в ограничениях задачи имеют вид «³». Двойственная - следующая: 2 y 1+4 y 2-6 y 3 ® max
Убеждаемся в этом точно так же, как и в предыдущем случае. При нахождении решения одной из двух двойственных задач по решению другой используют следующие теоремы двойственности, вторую из которых для удобства мы сформулируем для пары симметричных двойственных задач: Теорема 1 (первая теорема двойственности). Значения целевых функций пары двойственных задач на их оптимальных планах совпадают. Теорема 2 (вторая теорема двойственности). Пусть X 0=( c 1 x 1+ c 2 x 2+…+ cnxn ® max b 1 y 1+ b 2 y 2+…+ bmym ® min
Тогда они связаны соотношениями
В силу второй теоремы для решения пары двойственных задач (1) и (2) достаточно поступить следующим образом: сначала решить одну из них, например (1), и по её решению |




 (где aik >0) будет минимальным. Это (i -е) уравнение будет ведущим: разделив его на коэффициент aik при xk, добиваемся, чтобы коэффициент при xk стал равным 1, а из остальных уравнений xk исключаем (применяем метод Жордана-Гаусса). Процесс продолжаем до тех пор, пока базис не будет содержать m переменных.
(где aik >0) будет минимальным. Это (i -е) уравнение будет ведущим: разделив его на коэффициент aik при xk, добиваемся, чтобы коэффициент при xk стал равным 1, а из остальных уравнений xk исключаем (применяем метод Жордана-Гаусса). Процесс продолжаем до тех пор, пока базис не будет содержать m переменных. =2 достигается в первом уравнении (при определении этого min второе уравнение не участвует, так как коэффициент при x 2 в нём равен 0), то x 2 включаем в базис, исключив его из третьего уравнения (для этого первое уравнение вычитаем из третьего):
=2 достигается в первом уравнении (при определении этого min второе уравнение не участвует, так как коэффициент при x 2 в нём равен 0), то x 2 включаем в базис, исключив его из третьего уравнения (для этого первое уравнение вычитаем из третьего):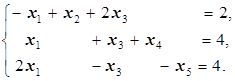
 =2 достигается в третьем уравнении. Поэтому третье уравнение делим на 2, затем прибавляем его к первому и вычитаем из второго:
=2 достигается в третьем уравнении. Поэтому третье уравнение делим на 2, затем прибавляем его к первому и вычитаем из второго: (*)
(*) - ck для всех k =0, 1, …, n. При этом D0 - это значение целевой функции при данном опорном плане, и D k =0 для всех базисных переменных xk (то есть последние вычислять необязательно, а достаточно сразу положить D k =0).
- ck для всех k =0, 1, …, n. При этом D0 - это значение целевой функции при данном опорном плане, и D k =0 для всех базисных переменных xk (то есть последние вычислять необязательно, а достаточно сразу положить D k =0).
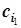



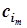
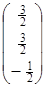 -2=1×
-2=1×  +0×
+0×  -2=1,
-2=1, -0=1×
-0=1× 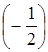 +0×
+0×  +(-3)×
+(-3)×  , а по ним - величины - qk D k.
, а по ним - величины - qk D k. =
= 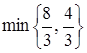 =
=  (достигается при x 4),
(достигается при x 4), =
=  =4, (достигается снова при x 4, то есть в любом случае x 4 будем выводить из базиса),
=4, (достигается снова при x 4, то есть в любом случае x 4 будем выводить из базиса), ,
,  , …,
, …,  ,
,  , …,
, …,  ) - оптимальное решение вспомогательной задачи, где x 1, x 2, …, xm - основные и дополнительные переменные (из задачи в каноническом виде), xm +1, xm +2, …, xm + s - искусственные переменные то (
) - оптимальное решение вспомогательной задачи, где x 1, x 2, …, xm - основные и дополнительные переменные (из задачи в каноническом виде), xm +1, xm +2, …, xm + s - искусственные переменные то ( ±
±  M, причём M - достаточно большое число. Поэтому при
M, причём M - достаточно большое число. Поэтому при 
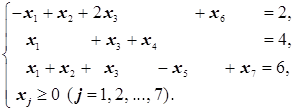
 =2. Поэтому искусственная переменная исключается из базиса, а вместо неё в базис включается x 1.
=2. Поэтому искусственная переменная исключается из базиса, а вместо неё в базис включается x 1.



 =
=  .
.
 ,
,  , …,
, …,  ) и Y 0=(
) и Y 0=( ,
,  , …,
, …,  ) - решения соответственно задач
) - решения соответственно задач (1) и
(1) и  (2).
(2). (3)
(3)


