
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Транспортная задача на min времениСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: Изучение теоретических и практических приёмов решения транспортных задач с нелинейной целевой функцией. Заменяя в транспортной задаче стоимость доставки на время доставки ti j и введя критерий min времени: min T=max{ t i j}, получим новую модель транспортной задачи с нелинейной целевой функцией. Задачу можно свести к обычной транспортной, применив метод запрещенных клеток. Метод запрещённых клеток.
Состоит из следующих шагов: 1. Находим опорное решение. 2. Из базисных клеток находим T = max ti j, и все клетки с большим временем – запрещаем для использования, 3. Улучшение плана распределительным методом. Достигается циклическим переносом из клеток xij с ti j= T в свободные клетки с меньшим временем. Допускается вхождение в цикл нескольких свободных клеток, помеченных знаком «+». 4. Переход ко второму пункту до тех пор, пока будет возможно построить цикл. Покажем решение задачи на минимум времени на примере. Пусть задана матрица перевозок и построен опорный план методом северо-западного угла (таблица 2.1).
Таблица 2.1. Опорное решение задачи на min T
T=max{ t i j}= t11 =10 и все клетки с большим временем запрещаем для использования, у нас это клетка x41 с t41=11. Цикл, включающий клетку x11, следующий: x21® x22® x12® x11® x21, после переноса по циклу получим новую таблицу 2.2 и время T=max{ t i j}= t45 =9 и к запрещенным добавляется клетка x11. Перенос по циклу x35® x45® x44® x34® x45, а затем x43® x45® x35® x33® x43 даёт следующую таблицу 9 с T=max{ t i j}= t44 =8 и клетки x45 и x25 включаются в число запрещенных.
Таблица 2.2. Промежуточное решение с T=9
Таблица 2.3. Промежуточное решение с T=8
Перенос по циклу x14® x12® x42® x44® x14, а затем x13® x12® x42® x43® x13, затем x32® x12® x35® x33® x32, затем x31® x32® x22® x21® x31 даёт следующую таблицу 10 с T=max{ t i j}= t33 =7 и клетки x12, x32, x34, x44, включается в число запрещенных. Попытка построить улучшающий цикл к успеху не приводит. Решение закончено. Таблица 2.4. Оптимальное решение, T=7
Практическая работа №3
ЗАДАЧА О НАЗНАЧЕНИЯХ
Цель работы: Изучение теоретических и практических приёмов решения транспортных задач с булевскими переменными. Если в обычной транспортной задаче положить запасы и потребности единичными (булевскими переменными), то получим специальный класс задач о назначениях. Задачу можно рассматривать как частный случай транспортной. Предложение и спрос в каждом пункте равно 1, т. е. ai=1, для всех i, bj=1 для всех j. Стоимость «перевозки» (прикрепления работы i к станку j) равна cij. Ниже в таблице 3.1 иллюстрируется общая структура задачи о назначениях. Прежде чем решать задачу методами, ассоциированными с транспортной моделью, необходимо «ликвидировать» дисбаланс, так что Задачу о назначениях можно представить следующим образом. Пусть xij =0, если j -я работа не выполняется i -м станком, xij =1, если j -я работа выполняется i -м станком. Теперь задача будет формулироваться так: найти min
Таблица 3.1. Задача о назначениях
Для иллюстрации задачи о назначениях рассмотрим пример с тремя работами и тремя станками (табл. 3.2). Исходное решение (полученное по правилу северо-западного угла) будет, очевидно, вырожденным. Таблица 3.2. Опорное решение
Эта особенность характерна для задачи о назначениях независимо от метода, используемого при получении начального базиса. Специфическая структура задачи о назначениях позволяет разработать эффективный метод ее решения. Покажем, как реализуется этот метод на примере приведенной выше задачи.
Решение через нуль-базис
Оптимальное решение задачи о назначениях не изменится, если к любой строке или столбцу матрицы стоимостей прибавить (или вычесть) постоянную величину. Этот факт можно доказать следующим образом. Если
Поскольку Приведенное соображение показывает, что если можно построить новую Если сначала рассмотреть строки табл. 3.2, то получим Заштрихованными квадратами в табл. 3.4 помечены элементы, соответствующие допустимому (и, следовательно, оптимальному) назначению (1, 1), (2, 3) и (3, 2) со стоимостью 5+12+13=30. Заметим, что эта стоимость равна p1+p2+p3+q3.
Таблица 3.3. Матрица стоимостей Таблица 3.4. Решение
К сожалению, не всегда удается определить допустимое назначение столь просто, как в приведенном примере. Поэтому требуются другие правила для нахождения оптимального решения. Пусть надо решить задачу о назначениях, в которой стоимость работ представлена в виде некоторой матрицы. Задача распределения работ сводится к построению математического аналога единичной матрицы, роль единиц в которой будут играть нули. Просматривая строки и столбцы, вычитаем минимальный элемент. Если в полученной матрице удаётся выделить нуль-базис, то решение закончено. Чтобы выделить нуль-базис нужно применить процедуру min-покрытия нулей. Для этого вычеркиваем нули матрицы min-количеством прямых, если количество прямых равно размерности матрицы стоимостей, то они и задают базис, если это не выполнено, то выбирается наименьший не вычеркнутый элемент. Этот элемент вычитается из всех не вычеркнутых и прибавляется к элементам на пересечении прямых, и процедура покрытия повторяется. После получения базиса: Z=åpi + åqj + å Wk, где pi - минимальные элементы по строкам, qj - минимальные элементы по столбцам, Wk- наименьшие не вычеркнутые элементы. Чтобы получить требуемое распределение работ можно применить следующую процедуру. В матрице определить минимальное количество нулей в строке и в столбце. Выбранный элемент распределяем, вычеркивая строку и столбец. К оставшейся матрице вновь применить указанную процедуру. Данная процедура одновременно отвечает на вопрос о размерности матрицы стоимостей. Если все работы распределены, то решение получено и оптимально.
Эти правила иллюстрируются на примере, приведенном в таблице 3.5. Выполняя те же начальные шаги, что и раньше, получим таблицу 3.6. В этом случае невозможно найти допустимое решение, состоящее из нулей. Дальнейшая процедура состоит в проведении минимального числа прямых через некоторые строки и столбцы с тем, чтобы все нули оказались вычеркнутыми. В табл.3.7 показано, как используется это правило. На следующем шаге выбирается наименьший не вычеркнутый элемент (C32=1). Этот элемент вычитается из каждого не вычеркнутого элемента и прибавляется к каждому элементу, стоящему на пересечении проведенных прямых. Таблица. 3.5. Исходная задача Таблица 3.6. Матрица с нулями
В результате получается табл. 3.8, которая соответствует оптимальному назначению (1, 1), (2, 3), (3, 2) и (4, 4). Суммарные затраты равны 1+10+5+5=21. Табл. 3.7. Покрытие нулей Табл. 3.8. Оптимальное решение
Заметим, что если на последнем шаге оптимальное решение не достигнуто, то процедуру проведения прямых следует повторять до тех пор, пока не будет получено допустимое решение. Практическая работа №4
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 822; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.103.119 (0.007 с.) |


 .
.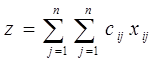 при ограничениях
при ограничениях
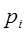 и
и  вычитаются из i -й строки и j -го столбца, то новые стоимости имеют вид
вычитаются из i -й строки и j -го столбца, то новые стоимости имеют вид  . Отсюда получается новая целевая функция:
. Отсюда получается новая целевая функция:
 , то
, то  . Отсюда следует, что минимизация исходной целевой функции z приводит к такому же решению, как минимизация z '.
. Отсюда следует, что минимизация исходной целевой функции z приводит к такому же решению, как минимизация z '. -матрицу с нулевыми элементами и эти нулевые элементы или их подмножество соответствуют допустимому решению, то такое решение будет оптимальным, поскольку стоимость не может быть отрицательной.
-матрицу с нулевыми элементами и эти нулевые элементы или их подмножество соответствуют допустимому решению, то такое решение будет оптимальным, поскольку стоимость не может быть отрицательной. -матрицу, представленную в табл.3.3. Вычитая
-матрицу, представленную в табл.3.3. Вычитая  из третьего столбца, последнюю матрицу можно преобразовать так, чтобы она имела больше нулей (табл. 3.4).
из третьего столбца, последнюю матрицу можно преобразовать так, чтобы она имела больше нулей (табл. 3.4).



