
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение задач линейного программирования с помощью игровых моделейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: Изучение теоретических и практических приёмов составления игровых моделей для задач линейного программирования.
Если игровая модель всегда сводится к паре моделей задач линейного программирования, то обратное утверждение неверно. Рассмотрим перевод задачи линейного программирования к игровой модели. В общем случае целевая функция z=∑ ci * xi Заменой переменных (ci * xi) / z= pi целевая функция приводится к виду 1=∑ pi, это основное условие перехода к игровой модели. Так как pi ≥ 0, то должно быть выполнено требование (ci * xi) / z ≥ 0 и z ≠ 0 ввиду невозможности деления на нуль. При xi ≥ 0, что обычно ставится одним из условий задач линейного программирования, основным требованием является sign(ci) * sign(z) ≥ 0. Если условие не выполняется, то можно построить неполную модель игры, принимая отрицательные pi равными нулю и тем самым полагая равными нулю соответствующие исходные переменные. Неполная модель дает верхнюю оценку целевой функции. Далее будем считать, что требование неотрицательности коэффициентов в целевой функции выполнено. Рассмотрим отдельно задачи на min и max. Пусть целевая функция min z=∑ ci * xi В ограничения вида
подставим xi =(pi * z) / ci, левые и правые части ограничений разделим на z и нормируем ограничения поделив каждое на bi (по условию bi положительно определённые коэффициенты). Ограничения с bj =0 из системы исключаем в дополнительные условия, которым должно удовлетворять конечное решение. Очевидно, что нормировка правой части ограничений может быть выполнена и в начале. В результате получим игровую модель
Учитывая, что в исходной задаче z → min, то η → max, так что здесь реализуется максиминный критерий для игрока А. Аналогично для линейной модели на max z=∑ ci * xi с ограничениями вида
подстановка и нормировка приводят к следующей игровой модели
Учитывая, что в исходной задаче z → max, то η → min, так что здесь реализуется минимаксный критерий для игрока B. Необходимо отметить, что вид экстремума меняется в двойственной задаче с одновременной заменой знака отношений в ограничениях. Игровая модель (матрица игры) одна и та же как для прямой, так и для двойственной задач, так как решения для игроков как раз и определяют свойство двойственности.
После решения игры (например, методом итераций) определяем решение исходной задачи линейного программирования с помощью восстановления цепочки замены переменных. Рассмотрим решение на примере известной из раздела линейного программирования задачи: найти max z= 2 x1 +3 x2 при ограничениях
Сравнивая вид неравенств в ограничениях с игровыми моделями выше, видим, что модель игры нужно строить как минимаксную для игрока B. Разделим целевую функцию на z и положим ее равной единице, т.е. 1=q1 + q2, откуда x1=(1/2) q1 z, x2=(1/3) q2 z и подстановка в ограничения после нормировки и деления на z даёт следующую игровую модель
На рисунке 9.1 приведено графическое решение игровой модели.
Экстремальная точка определяется первым и вторым уравнением. С учетом условия нормировки вероятностей имеем три уравнения для трех переменных. Их решение дает q1 = 4/19 q2 = 15/19, ν = 3/38, обратная подстановка приводит к исходным данным: x1 = 4/3, x2 = 10/3, z = 38/3, что совпадает с ранее найденным решением. Заметим, что результирующая матрица игры состоит всего из двух первых строк. Рассмотрим теперь двойственную задачу. Модель для нее: min z=6y1+8y2+y3+2y4 при ограничениях
После нормировки
т.е. имеем maxmin и модель для игрока A. Из z y1=1/6p1z, y2=1/8p2z, y3=p3z, y4=1/2p4z и подстановка в ограничения после деления на z дает следующие соотношения
Соответствующая матрица игры совпадает с ранее найденной.
Модель с положительными и отрицательными коэффициентами в целевой функции
Оценка решения
Наиболее просто отыскивается оценка решения. Считая, что в целевой функции должны быть положительные слагаемые (так как соответствующие им вероятности есть положительные числа), можно положить равными нулю переменные с отрицательными слагаемыми и решить полученную задачу. Рассмотрим модель с положительными и отрицательными коэффициентами в целевой функции. Пусть задана линейная модель в виде: Min z = 5x1-2x3, ограничения По виду ограничений соответствующая игровая модель - minmax для игрока B, поэтому вид экстремума нужно изменить. Так как min z = max(-z), то получим целевую функцию в виде max z = -5x1+2x3. Первый коэффициент отрицательный, поэтому адекватную линейной модели игровую модель построить нельзя. Полагая q1=0, и, следовательно, x1=0, получим q2=0, q4=0, x2=0,x4=0 соответствующая игровая модель
Минимальный проигрыш соответствует нижнему элементу матрицы, решение получено в чистых стратегиях: q3 = 1, ν = 1/10, max(-z)=10, x1 =0, x3=1/2 q3 * 10 = 5, z = -10. Подставим найденное решение в исходную систему ограничений: -x2 + 2*5 ≤ 2, 5 +x4 ≤ 5. Отсюда x4 =0, x2 = 8. Решив задачу симплекс-методом, получим X = (0, 8, 5, 0, 0, 0, 7), min z = -10. В общем случае нужно помнить, что мы получаем оценку решения, но, заметьте, насколько прост метод.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 547; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.236.144 (0.007 с.) |

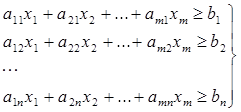
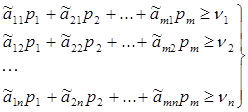 , ∑ pi =1.
, ∑ pi =1.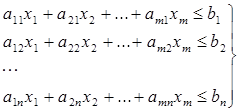
 , ∑ qi =1.
, ∑ qi =1. ,
,  .
.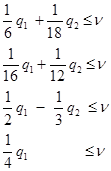 , соответствующая матрица игры A=
, соответствующая матрица игры A= 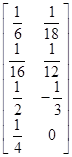
 Рис 9.1. Графическое решение задачи
Рис 9.1. Графическое решение задачи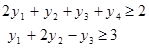 ,
, 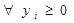 .
.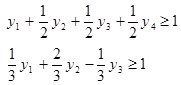 ,
,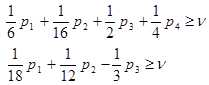 .
. ,
, 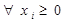 .
.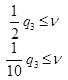 и матрица игры A=
и матрица игры A=  .
.


