
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи теории игр в экономике, финансах и бизнесеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Задачи теории игр в экономике, финансах и бизнесе Теория игр – раздел современной математики, изучающий математические модели принятия решений в т.н. конфликтных ситуациях. Во многих задачах финансово-экономической сферы возникает необходимость принятия решения. Проблема принятия решения осложняется тем, что ее приходится решать в условиях неопределенности. В условиях полной определенности теоретические и практические выводы носят однозначный характер и, таким образом, представляют четкое описание ситуации в рамках рассматриваемой задачи. В условиях же недостаточной информированности или полной неопределенности результаты анализа уже не обладают такой четкостью и однозначностью. Попытка количественного анализа финансово-экономических ситуаций и принятия на их основе решения привела к созданию специальных экономико-математических методов обоснования выбора решений в условиях рыночной неопределенности. Эти методы позволяют находить количественные характеристики экономических процессов, что влечет за собой возможность наиболее полного сравнения исследуемых явлений. При выборе решения в условиях неопределенности всегда присутствует фактор действия наудачу без обоснованной уверенности в успехе. Он неизбежно присутствует в различных хозяйственных операциях (коммерческий риск), в выполнении предприятием определенного заказа (производственный риск), в выполнении фирмой финансовых обязательств перед инвестором (кредитный риск), в решении купить акции или другие ценные бумаги (инвестиционный риск), в решениях положить деньги в банк (финансовый риск). Математические методы обоснования решений дают возможность анализа вариантов решения с целью уменьшения риска, которое иногда достигается за счет получения дополнительной информации. Математизация содержательных финансово-экономических задач о принятии решениях в условиях неопределенности приводит к соответствующим экономико-математическим моделям и методам, теоретический аспект которых составляет теорию игр. Таким образом, задачами теории игр в экономике являются задачи о выборе решений в условиях экономической неопределенности.
2. Основные понятия и определения теории игр Конфликтная ситуация характеризуется следующими чертами: · наличие заинтересованных сторон (в качестве которых могут выступать потребители, фирмы, отдельные страны, различные таможенные, торговые, финансовые и экономические союзы) · существование возможных действий каждой из сторон (выбор объема потребления, выбор дивидендной политики, различные способы комплектования инвестиционного портфеля, выбор объемов выпуска, недопущение на национальный рынок некоторых товаров по политическим или экономическим соображениям) · интересы сторон (удовлетворение различных политических, финансовых, экономических потребностей, монопольные прибыли, вытеснение конкурентов с рынка сбыта) Стратегия – любое возможное действие игрока. Игровая ситуация – результат выбора каждым из игроков своей стратегии. Множество игровых ситуаций – все возможные варианты игровых ситуаций. Образует ситуационное пространство игры. Игра – упрощенная, формализованная модель конфликта. Важным отличием игры от реального конфликта является наличие жёстко определённых правил поведения. Игроки – заинтересованные в конфликте стороны. Платежная матрица – матрица, элементами корой являются выигрыши (проигрыши) игрока. Антагонистическая игра – игра с нулевой суммой, в которой выигрыш одного игрока равен проигрышу другого. FA=-FB, где F – функция выигрыша. Антагонистические игроки Страховщик и страхователь На рынке есть страховщик и страхователь. Эта игра антагонистическая, так как выигрыш одного игрока равен проигрышу другого. Взаимодействие этих сторон можно рассматривать, как игру, потому что есть конфликт интересов. У каждого игрока есть свои стратегии. И они нацелены на максимизацию своего выигрыша, либо минимизацию проигрыша.
Игра» - математическая модель антагонистической ситуации
Понятие смешанной стратегии Смешанная стратегия игрока – стратегия игрока, состоящая в случайном выборе им одной из своих чистых стратегий с определённой вероятностью. Таким образом, смешанная стратегия игрока представляет собой дискретную случайную величину, значениями которой являются номера его чистых стратегий. При условии, что множество
То же относится и к смешанным стратегиям игрока В:
Каждую чистую стратегию 𝐴𝑖, 𝑖 = 1,..., 𝑚, игрока 𝐴 можно рассматривать как смешанную стратегию (1)
в которой чистая стратегия 𝐴𝑖 выбирается с вероятностью 𝑝𝑖= 1, а все остальные чистые стратегии с вероятностью, равной нулю. Поэтому конечное множество Каждую смешанную стратегию можно представить линейной комбинацией чистых стратегий с коэффициентами, являющимися координатами данной смешанной стратегии: 𝑃 = (𝑝1,...,𝑝𝑚) = ∑𝑚𝑖=1 𝑝𝑖𝐴𝑖. (2) Показатель эффективности смешанной стратегии игрока А относительно множества чистых стратегий игрока В. соотношение между показателями эффективности смешанной стратегии игрока А относительно множеств смешанных и чистых стратегий игрока В
Число
называется показателем эффективности смешанной стратегии Теорема. Показатели эффективности любой смешанной (в частности, чистой) стратегии
Доказательство. Так как И, следовательно
Докажем противоположное неравенство. Пусть
Тогда используя формулы
Для любых
Последнее неравенство и
противоположны, следовательно Показатель неэффективности смешанной стратегии игрока В относительно множества чистых стратегий игрока В. Соотношение между показателями неэффективности смешанной стратегии игрока В относительно множеств смешанных и чистых стратегий игрока А
Число
называется показателем неэффективности смешанной стратегии Q игрока B относительно множества Теорема. Показатели неэффективности любой смешанной (в частности, чистой) стратегии
Доказательство. Так как И, следовательно
Докажем противоположное неравенство. Пусть Тогда используя формулы
Для любых
Последнее неравенство и
противоположны, следовательно Теорема Пусть V-цена игры, Н(Р,Q) – выигрыш-функция, Для того чтобы стратегия Р0 игрока А была оптимальной, необходимо и достаточно, чтобы Н(Р0, Док-во: Достаточно установить эквивалентность нер-в Пусть справедливо нер-во (2). Т.к. это нер-во имеет место для любой стр-гии Q Теперь пусть имеет место быть нер-во (1). Тогда по ф-ле с учетом того, что
Теорема Пусть V-цена игры, Н(Р,Q) – выигрыш-функция, Для того чтобы стратегия Q0 игрока B была оптимальной, необходимо и достаточно, чтобы Док-во: Достаточно установить эквивалентность нер-в Пусть справедливо нер-во (2). Т.к. это нер-во имеет место для любой стр-гии P Теперь пусть имеет место быть нер-во (1). Тогда по ф-ле с учетом того, что
Определения активных и пассивных чистых стратегий и теорема об активных стратегиях Пусть 𝑃0=(𝑝10,…,𝑝m0) – оптимальная смешанная стратегия игрока А. В общем случае, некоторые из вероятностей 𝑝10,…,𝑝m0 могут быть равными нулю. Если 𝑝i0=0, где i – одно из чисел 1,…,m, то в оптимальной смешанной стратегии 𝑃0=(𝑝10,…,𝑝m0) чистая стратегия 𝐴𝑖 не участвует и потому называется пассивной. Чистые стратегии 𝐴𝑖, входящие в оптимальную стратегию 𝑃0 с положительной вероятностью 𝑝i0>0, называются активными стратегиями игрока А. Аналогично определяются активные стратегии игрока В. Теорема (об активных стратегиях). Пусть V – цена игры и 𝑃0=(𝑝10,…,𝑝m0), 𝑄0=(𝑞10,…,𝑞n0) - оптимальные стратегии соответственно игроков А и В. Тогда справедливы следующие утверждения. 1. Для любой активной стратегии 𝐴k,(𝑘𝜖{1,…,𝑚}) игрока А выполняется равенство 𝐻(𝐴k,𝑄0)=𝑉 2. Для любой активной стратегии 𝐵l (𝑙𝜖{1,…,𝑛}) игрока В выполняется равенство 𝐻(𝑃0,𝐵l)=𝑉 Основные понятия игры с природой. Матрица выигрышей сознательного игрока Во многих задачах финансово-экономической сферы принятие решения осложняется наличием неопределенности, заключающейся в неполноте информации об окружающей среде. Такую неопределенность могут порождать различные причины. Поэтому в таких задачах принятие решения зависит от реальных условий, которые называют в соответствующей математической модели «природой». Саму же модель называют «игрой с природой». «Природа» может выступать как антагонистическая сторона, а может как кооперативная среда. Игру с природой можно определить как парную игру, в которой сознательный игрок А, заинтересованный в наиболее выгодном для него исходе игры, выступает против участника, совершенно безразличного к результату – природа (обозначим его П). Игра с природой — математическая модель ситуаций, когда осознанно действует только один игрок (обозначим его через А), принимающий решение, и когда исход игры зависит не только от решений игрока А, но и от состояния “природы” (обозначим через П), т. е. не от сознательно противодействующего противника, а от объективной, невраждебной действительности. Природа – это: 1. объективная действительность; 2. игрок, но не противник игрока А, потому что не действует осознанно против игрока А, а принимает неопределенным образом то или иное свое состояние, не преследуя конкретной цели и безразлично к результату игры. Статистик – игрок в игре с природой, действующий осознанно, т.е. лицо, принимающее решение (игрок А). Одним из важных предположений в теории игр с природой является предположение о том, что в любой момент времени природа П может находиться только в одном (но неизвестно, в каком) из n состояний П1, П2, …, Пn, то есть состояния природы разделены между собой во времени. Совокупность Для описания игры с природой необходимо также множество стратегий игрока A: Показателем благоприятности состояния Риском Матрица рисков Пример для матрицы выигрышей.
Из наибольшего числа каждого столбца вычитаем каждое число данного столбца. Стратегия S1 является оптимальной по критерию Байеса относительно рисков, так как именно у этой стратегии наименьший показатель неэффективности (0,6).
Пример для матрицы выигрышей.
Из наибольшего числа каждого столбца вычитаем каждое число данного столбца. Стратегия S1 является оптимальной по критерию Байеса относительно рисков, так как наименьший показатель неэффективности именно у этой стратегии (0,6).
Стр 145
Стр 167 Стр 177 Задачи теории игр в экономике, финансах и бизнесе Теория игр – раздел современной математики, изучающий математические модели принятия решений в т.н. конфликтных ситуациях. Во многих задачах финансово-экономической сферы возникает необходимость принятия решения. Проблема принятия решения осложняется тем, что ее приходится решать в условиях неопределенности. В условиях полной определенности теоретические и практические выводы носят однозначный характер и, таким образом, представляют четкое описание ситуации в рамках рассматриваемой задачи. В условиях же недостаточной информированности или полной неопределенности результаты анализа уже не обладают такой четкостью и однозначностью. Попытка количественного анализа финансово-экономических ситуаций и принятия на их основе решения привела к созданию специальных экономико-математических методов обоснования выбора решений в условиях рыночной неопределенности. Эти методы позволяют находить количественные характеристики экономических процессов, что влечет за собой возможность наиболее полного сравнения исследуемых явлений. При выборе решения в условиях неопределенности всегда присутствует фактор действия наудачу без обоснованной уверенности в успехе. Он неизбежно присутствует в различных хозяйственных операциях (коммерческий риск), в выполнении предприятием определенного заказа (производственный риск), в выполнении фирмой финансовых обязательств перед инвестором (кредитный риск), в решении купить акции или другие ценные бумаги (инвестиционный риск), в решениях положить деньги в банк (финансовый риск). Математические методы обоснования решений дают возможность анализа вариантов решения с целью уменьшения риска, которое иногда достигается за счет получения дополнительной информации. Математизация содержательных финансово-экономических задач о принятии решениях в условиях неопределенности приводит к соответствующим экономико-математическим моделям и методам, теоретический аспект которых составляет теорию игр. Таким образом, задачами теории игр в экономике являются задачи о выборе решений в условиях экономической неопределенности.
2. Основные понятия и определения теории игр Конфликтная ситуация характеризуется следующими чертами: · наличие заинтересованных сторон (в качестве которых могут выступать потребители, фирмы, отдельные страны, различные таможенные, торговые, финансовые и экономические союзы) · существование возможных действий каждой из сторон (выбор объема потребления, выбор дивидендной политики, различные способы комплектования инвестиционного портфеля, выбор объемов выпуска, недопущение на национальный рынок некоторых товаров по политическим или экономическим соображениям) · интересы сторон (удовлетворение различных политических, финансовых, экономических потребностей, монопольные прибыли, вытеснение конкурентов с рынка сбыта) Стратегия – любое возможное действие игрока. Игровая ситуация – результат выбора каждым из игроков своей стратегии. Множество игровых ситуаций – все возможные варианты игровых ситуаций. Образует ситуационное пространство игры. Игра – упрощенная, формализованная модель конфликта. Важным отличием игры от реального конфликта является наличие жёстко определённых правил поведения. Игроки – заинтересованные в конфликте стороны. Платежная матрица – матрица, элементами корой являются выигрыши (проигрыши) игрока. Антагонистическая игра – игра с нулевой суммой, в которой выигрыш одного игрока равен проигрышу другого. FA=-FB, где F – функция выигрыша. Антагонистические игроки Страховщик и страхователь На рынке есть страховщик и страхователь. Эта игра антагонистическая, так как выигрыш одного игрока равен проигрышу другого. Взаимодействие этих сторон можно рассматривать, как игру, потому что есть конфликт интересов. У каждого игрока есть свои стратегии. И они нацелены на максимизацию своего выигрыша, либо минимизацию проигрыша.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1486; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.012 с.) |



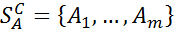 чистых стратегий игрока А известно, каждая его смешанная стратегия Р определяется вероятностями
чистых стратегий игрока А известно, каждая его смешанная стратегия Р определяется вероятностями  , с которыми выбираются игроком А соответствующие чистые стратегии. Поэтому смешанную стратегию Р можно отождествить с m-мерными вектором (
, с которыми выбираются игроком А соответствующие чистые стратегии. Поэтому смешанную стратегию Р можно отождествить с m-мерными вектором ( , т.е.
, т.е.

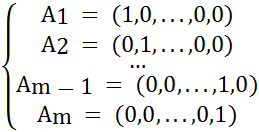
 , состоящее из 𝑚 чистых стратегий игрока 𝐴, является собственным при (𝑚 ≥ 2) подмножеством бесконечного множества его смешанных стратегий 𝑆А.
, состоящее из 𝑚 чистых стратегий игрока 𝐴, является собственным при (𝑚 ≥ 2) подмножеством бесконечного множества его смешанных стратегий 𝑆А.
 игрока А относительно множества
игрока А относительно множества  чистых стратегий игрока В. В частности, если
чистых стратегий игрока В. В частности, если  – чистая стратегия, то
– чистая стратегия, то  - показатель эффективности чистой стратегии
- показатель эффективности чистой стратегии  (относительно множества
(относительно множества  и
и 
 то
то 

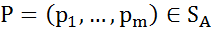 и
и
 и
и  и
и  , получим неравенство
, получим неравенство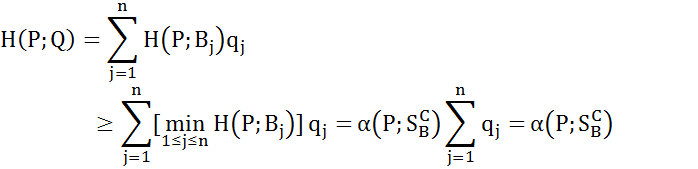
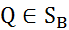 . Так как правая часть этого неравенства не зависит от Q, то из него с учетом
. Так как правая часть этого неравенства не зависит от Q, то из него с учетом  будем иметь
будем иметь


 чистых стратегий игрока A. В частности, если
чистых стратегий игрока A. В частности, если  – чистая стратегия, то
– чистая стратегия, то  - показатель неэффективности чистой стратегии
- показатель неэффективности чистой стратегии 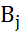 (относительно множества
(относительно множества  и
и 
 то
то 

 и
и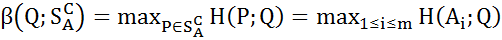 и
и  , получим неравенство
, получим неравенство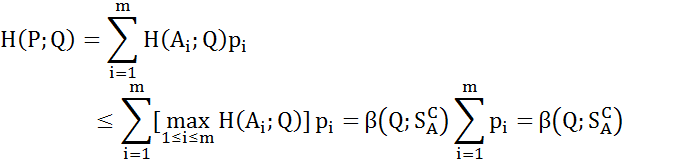
 будем иметь
будем иметь

 =
=  – множества чистых стратегий игрока В.
– множества чистых стратегий игрока В. )
)  V, j=1,…,n (1)
V, j=1,…,n (1) SB (2)
SB (2) SB игрока В, то оно, в частности, будет справедливым и для его чистых стратегий Вj
SB игрока В, то оно, в частности, будет справедливым и для его чистых стратегий Вj  , j=1,…,n, т.е. нер-во (1) имеет место =>
, j=1,…,n, т.е. нер-во (1) имеет место => 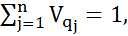 получим
получим Q
Q  – – мн-ва чистых стратегий игрока А.
– – мн-ва чистых стратегий игрока А. V для любого P
V для любого P  SA игрока A, то оно, в частности, будет справедливым и для его чистых стратегий Ai
SA игрока A, то оно, в частности, будет справедливым и для его чистых стратегий Ai  , i=1,…,m, т.е. нер-во (1) имеет место =>
, i=1,…,m, т.е. нер-во (1) имеет место =>  получим
получим P
P 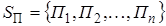 состояний природы П формируется либо на основе имеющегося опыта анализа состояний природы, либо в результате предположений и интуиции экспертов.
состояний природы П формируется либо на основе имеющегося опыта анализа состояний природы, либо в результате предположений и интуиции экспертов.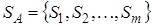 .
.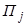 природы для увеличения выигрыша называется наибольший выигрыш при этом состоянии, т.е. наибольший элемент в j-м столбце матрицы игры:
природы для увеличения выигрыша называется наибольший выигрыш при этом состоянии, т.е. наибольший элемент в j-м столбце матрицы игры: 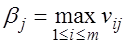 ,
, 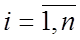 ,
, 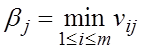
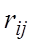 игрока A при выборе им стратегии
игрока A при выборе им стратегии 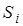 в условиях состояния
в условиях состояния 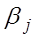 состояния природы
состояния природы 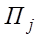 и выигрышем
и выигрышем 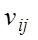
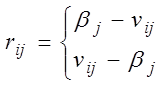
 ,
, 
 ,
, 
 ,
, 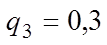
 ,
, 

 ,
, 






