
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ситуация равновесия. Седловая точка выигрыш-функции игрока А. Седловая точка матрицы выигрышей (платежной матрицы)Содержание книги
Поиск на нашем сайте
Ситуация (Ak, Bl) называется равновесной, если она удовлетворительна для каждого из игроков А и В то есть если выполняются неравенства Таким образом, двойное нер-во (1) и двойное равенство (2) эквивалентны. Выигрыш Матрица игры может обладать несколькими седловыми точками или не обладать ими в целом. Свойство равнозначности седловых точек матрицы игры
Седловые точки обладают важными свойствами. Одно из них – свойство равнозначности. Теорема «свойство равнозначности седловых точек». Если Док-во: Т.к Из неравенств выше, следует неравенство Применив аналогичные рассуждения сначала к седловой точке Свойство взаимозаменяемости седловых точек матрицы игры. Теорема «св-во взаимозаменяемсотиседловых точек» Если Док-во. т.к.
с другой стороны по опр. показателя эффективности и показ. неэфф-ти имеем (2):
Из равенства (1) и неравенства(2) следует,что
а это означает, что Замечание. Теорема сформулирована для случая, когда взаимозаменяются вторые индексы седловых точек Если первые индексы седловых точек Стратегии, оптимальные во множестве чистых стратегий. Полное (общее) и частное решение игры в чистых стратегиях
Стратегии
Если нижняя цена α = верхней цене β, то их общее значение γ=α=β называется ценой игры в чистых стратегиях. Совокупность Критерий существования цены игры в чистых стратегиях Теорема. Для того чтобы существовала цена игры в чистых стратегиях, т.е. для того чтобы нижняя цена игры Доказательство. Необходимость. Пусть существует цена игры в чистых стратегиях, т.е. нижняя цена игры Пусть Рассмотрим элемент Из определений показателя эффективности
откуда в силу
Достаточность. Пусть существует седловая точка
Отсюда по определению нижней и верхней цен игры т.е.
|
|||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1011; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.12.236 (0.009 с.) |

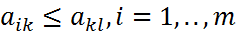 и
и 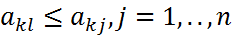 :
:  (1) или равенства
(1) или равенства  и
и  :
:  (2)
(2) , соответствующий ситуации равновесия (Ak, Bl), называют седловой точкой матрицы игры. Таким образом, элемент
, соответствующий ситуации равновесия (Ak, Bl), называют седловой точкой матрицы игры. Таким образом, элемент 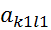 и
и 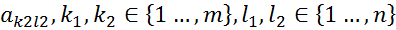 –седловые точки, то
–седловые точки, то 
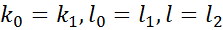 имеем
имеем 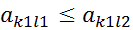 т.к.
т.к.  ,получим
,получим 
 (1)
(1) , а затем к седловой точке
, а затем к седловой точке  (2), неравенства (1) и (2) доказывают равенство
(2), неравенства (1) и (2) доказывают равенство  и
и  ,
, 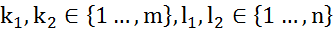 - седловые точки, то и
- седловые точки, то и 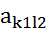 и
и 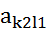 - также седловые точки
- также седловые точки и
и  - седловые точки, то по теореме о равнозначности седловых точек справедливо равенство
- седловые точки, то по теореме о равнозначности седловых точек справедливо равенство  из которого получим
из которого получим (1)
(1)
 ,
, .Если у седловых точек
.Если у седловых точек 
 и
и  , то взаимозаменяемость вторых индексов не приводит к новым седловым точкам.То же относится к седловым точкам с равными вторыми индексами при взаимозаменяемости первых.
, то взаимозаменяемость вторых индексов не приводит к новым седловым точкам.То же относится к седловым точкам с равными вторыми индексами при взаимозаменяемости первых. игроков A и B соответственно, создающие равновесную ситуацию
игроков A и B соответственно, создающие равновесную ситуацию  или, другими словами, соответствующие седловой точке
или, другими словами, соответствующие седловой точке  , называются оптимальными.
, называются оптимальными. множеств
множеств  чистых оптимальных стратегий игрока A и B и цены игры γ называется полным решением игры в чистых стратегиях, а совокупность {Ak, Bl, γ} какой-нибудь пары чистых оптимальных стратегий
чистых оптимальных стратегий игрока A и B и цены игры γ называется полным решением игры в чистых стратегиях, а совокупность {Ak, Bl, γ} какой-нибудь пары чистых оптимальных стратегий  и цена игры γ называется частным решением игры в чистых стратегиях. Цена игры в чистых стратегиях γ (если она существует) представляет собой значение выигрыша игрока А, кот. он не может увеличить, если игрок В придерживается своей оптимальной стратегии, и значение проигрыша игрока В, кот. последнее не может уменьшить при условии, что игрок А действует по своей оптимальной стратегии.
и цена игры γ называется частным решением игры в чистых стратегиях. Цена игры в чистых стратегиях γ (если она существует) представляет собой значение выигрыша игрока А, кот. он не может увеличить, если игрок В придерживается своей оптимальной стратегии, и значение проигрыша игрока В, кот. последнее не может уменьшить при условии, что игрок А действует по своей оптимальной стратегии.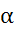 равнялась верхней ценен игры
равнялась верхней ценен игры  , необходимо и достаточно существование у матрицы этой игры седловой точки.
, необходимо и достаточно существование у матрицы этой игры седловой точки.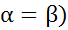 .
. максиминная стратегия игрока А, а
максиминная стратегия игрока А, а  минимаксная стратегия игрока В. Тогда
минимаксная стратегия игрока В. Тогда 
 стоящий на пересечении k-й строки и l-го столбца матрицы игры.
стоящий на пересечении k-й строки и l-го столбца матрицы игры. стратегии Ak и показателя неэффективности
стратегии Ak и показателя неэффективности  стратегии Вl будем иметь:
стратегии Вl будем иметь: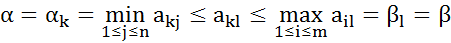
 получаем равенство
получаем равенство , которое обозначает, что элемент
, которое обозначает, что элемент  является седловой точкой.
является седловой точкой.

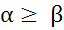 . Но
. Но  и потому
и потому 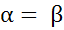 , т.е. существует цена игры в чистых стратегиях.
, т.е. существует цена игры в чистых стратегиях.


