
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Максимаксный критерий оптимальности стратегий во множестве чистых стратегийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Является противоположностью критерия Вальда. Представляет собой частный случай обобщенного критерия Гурвица относительно выигрышей, когда коэф. выбираются следующим образом: Оптимальной среди чистых стратегий по максимаксному критерию является стратегия Аio с максимальным показателем эффективности:
Т.е. стратегия, максимальный выигрыш при которой максимален среди максимальных выигрышей всех чистых стратегий. Поэтому оптимальной будет стратегия, при которой (хотя бы) один из выигрышей является максимальным среди выигрышей всех чистых стратегий.Оптимальная по максимаксному критерию стратегия гарантирует игроку А возможность наибольшего выигрыша, равного максимаксу. Для максимаксного критерия показатели пессимизма и оптимизма равны соответственно Максимаксный критерий оптимальности смешанных стратегий В экономике нередки обстоятельства, вынуждающие пользоваться этим критерием осознанно, например, в ситуации, когда перед игроком А стоит следующий выбор: получить наибольший выигрыш или стать банкротом. Данный подход распространим к принятию решения на смешанные стратегии Р=(р1, р2,.....,pm). Показатель эффективности смешанной стратегии Р по maxmax критерию или М - показателем эффективности стратегии Р (обозначается через М (Р)): М(Р) = max{H(P;Пj): j=1,2,..,n}. Цена игры в смешанных стратегиях по maxmax критерию - наибольший из показателей эффективности М(Р) всех смешанных стратегиях Р Є S (обозначается как Ms). Ms=maх{M(P): Р Є S}= max{max{H(P;Пj): j=1,2,..,n}:Р Є S} Данное равенство говорит о том, что цена игры в смешанных стратегиях есть максимакс в смешанных стратегиях, т.е. максимальный выигрыш игрока А среди выигрышей при всех смешанных стратегиях Р Є S. Теорема 1.12.1. В любой игре с природой существует стратегия, оптимальная во множестве смешанных стратегий по максимаксному критерию.
Теорема 1.12.2. По максимаксному критерию цены игры в смешанных и чистых стратегиях равны: Ms= Msc Следствие 1.12.1 (из теоремы 1.12.2). Чистая стратегия (ЧС), оптимальная во множестве ЧС по максимаксному критерию, является оптимальной по тому же критерию и во множестве СС. Следствие 1.12.2 (из следствия 1.12.1) В любой игре с природой существует чистая стратегия, оптимальная по максимаксному критерию во множестве смешанных стратегий. Теорема 1.12.3. Для того чтобы смешанная стратегия Р=(р1, р2,.....,pm) со спектром supp P ={ i1,i2,...,ik },1≤k≤m, была оптимальна по максимальному критерию во множестве СС необходимо и достаточно выполнение следующих 2 условий: a. У природы существует {i1,i2,...,ik}-состояние относительно максимального критерия; b. Показатели эффективности ЧС Аi1, Ai2,..., Aik равны цене игры по максимальному критерию. Следствие 1.12.3 (из теоремы 1.12.3) Если выполнять условия a и b, то любая СС Р=(р1, р2,.....,pm) со спектором supp P *{ i1,i2,...,ik }, 1≤k≤m, будет оптимальной по максимальному критерию во множестве S СС. Теорема 1.12.4. Множество SO(M) CC, оптимальных по максимаксному критерию во множестве S СС, является объединением выпуклых оболочек conv(SC) O(M)(j), j=1,2,..,n: SO(M) = Множество SO(M) смешанных оптимальных стратегий по максимаксному критерию является собственным подмножеством выпуклой оболочки conv(SC) O(M) множества чистых оптимальных стратегий по тому же критерию, т.е. SO(M) ⊂ conv(SC) O(M) и SO(M) ≠ conv(SC) O(M). Теорема о соотношении множеств стратегий, оптимальных во множестве чистых и во множестве смешанных стратегий по максимаксному критерию Теорема: по максимаксному критерию цены игры в смешанных и в чистых стратегиях равны MS=MSC Следствие: чистая стратегия, оптимальная во множестве чистых стратегий по максимаксному критерию, является оптимальной по тому же критерию во множестве смешанных стратегий.
|
|||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 830; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.170.2 (0.011 с.) |


 для матрицы выигрышей,
для матрицы выигрышей, для матрицы потерь.
для матрицы потерь.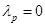 ,
,  . Таким образом, максимаксный критерий является критерием крайнего оптимизма, так как ориентирует ЛПР на наилучшее, благоприятнейшее для него состояния природы и, следовательно, на порой неоправданно легкомысленное поведение при выборе стратегий. Вместе с тем, в некоторых ситуациях этим критерием пользуются осознанно, например, в ситуации когда перед игроком стоит дилемма: либо получить наибольший выигрыш, либо стать банкротом.
. Таким образом, максимаксный критерий является критерием крайнего оптимизма, так как ориентирует ЛПР на наилучшее, благоприятнейшее для него состояния природы и, следовательно, на порой неоправданно легкомысленное поведение при выборе стратегий. Вместе с тем, в некоторых ситуациях этим критерием пользуются осознанно, например, в ситуации когда перед игроком стоит дилемма: либо получить наибольший выигрыш, либо стать банкротом.  O(M)(j)
O(M)(j)


