
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитическое решение игры без седловой точки, задаваемой симметрической и двоякосимметрической матрицей второго порядкаСодержание книги
Поиск на нашем сайте
Если матрица А размером 2*2 симметрическая, т.е. Замечание. Симметричность матрицы А никак не связана с существованием у этой матрицы седловых точек. Если матрица игры А размером 2*2 двоякокосимметрическая, т.е. V= Замечание. Двоякосимметрическая квадратная матрица 2-го порядка не имеет седловых точек, за исключением случая, когда все ее элементы равны, и в этом случае каждый элемент является седловой точкой. 47. Геометрический метод нахождения оптимальных смешанных стратегий игрока А и цены игры в смешанных стратегиях в игре размерности
Решению этой игры можно дать хорошо обозримую геометрическую интерпретацию, в основе которой лежит изображение смешанных стратегий каждого из игроков точками отрезка [0, 1] горизонтальной числовой прямой (одномерного пространства).
Алгоритм «А». 1. Берем горизонтальный отрезок [0, 1], на котором для определенности положено a 22 <a 11 <a 21 <a 12 2. В концах отрезка [0, 1] проводим к нему два перпендикуляра: левый, соответствующий стратегии А1 и правый, соответствующий стратегии А2. 3. На левом перпендикуляре от точки 0 его пересечения с отрезком [О, 1] откладываем (как на вертикальной числовой оси) элементы a 11 и a 12первой строки матрицы А. 4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0, 1] откладываем (как на вертикальной числовой оси) элементы a 22 и а 21 второй строки матрицы А. Замечания к пунктам 1, 3, 4: масштабы на левом и правом перпендикулярах должны быть одинаковы, не обязательно совпадающие с масштабом горизонтального отрезка [0,1]. 5. Соединяем точки, изображающие элементы с одинаковыми вторыми индексами, т.е. элементы, стоящие в одном и том же столбце матрицы А. В результате получаем отрезки a11a21 и a12a22 6. Если отрезки a11a21 и a12a22 неубывающие, то стратегия А2 доминирует стратегию А1 Если отрезки a11 a21 и a12a22 возрастающие, то стратегия А2 строго доминирует стратегию А1 7. Если отрезок a11a21 лежит не ниже отрезка a12a22, то стратегия В2 доминирует стратегию В1. Если отрезок a11a21 лежит выше отрезка a12a22 и не пересекается с ним, то стратегия В2 доминирует стратегию В1. 8. Находим нижнюю огибающую отрезков a11a21 и a12a22 9. Находим наивысшие точки нижней огибающей. 10. Проектируем их ортогонально на горизонтальный отрезок [0,1]. 11. Полученные проекции р° определяют оптимальные стратегии Р° = (1 — р°,р°) игрока А. 12. Ордината наивысшей точки огибающей равна цене игры V. 13. Верхний из двух концов нижней огибающей (лежащих на перпендикулярах) есть Нижняя цена игры в чистых стратегиях а. 14. Нижний из двух верхних концов отрезков a11a21 и a12a22 есть верхняя цена игры в чистых стратегиях р. 15. Если элемент является нижним на перпендикуляре, где он лежит, и верхним концом отрезка a11a21 или a12a22, на котором он лежит, то этот элемент является седловой точкой. В этом случае чистая стратегия игрока В, номер которой совпадает со вторым индексом седловой точки, является оптимальной. Пункт 15 алгоритма «А» дает возможность достаточно просто геометрически выявить оптимальную чистую стратегию игрока В в случае, если матрица игры содержит седловую точку. 48. Геометрический метод нахождения цены игры размера
1. Берем горизонтальный отрезок [0, 1], на котором для определенности положено а22 < а11 < а21 < а12. 2. В концах отрезка [0, 1] проводим к нему два перпендикуляра: левый, соответствующий стратегии В1 и правый, соответствующий стратегии В2. 3. На левом перпендикуляре от точки 0 его пересечения с отрезком [О, 1] откладываем (как на вертикальной числовой оси) элементы а11 и а21 первого столбца матрицы А. 4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0, 1] откладываем (как на вертикальной числовой оси) элементы а12 и а22 второго столбца матрицы А. Замечания к пунктам 1, 3, 4: масштабы на левом и правом перпендикулярах должны быть одинаковы, не обязательно совпадающие с масштабом горизонтального отрезка [0, 1]. 5. Соединяем точки, изображающие элементы с одинаковыми первыми индексами, т.е. элементы, стоящие в одной и той же строке матрицы А. В результате получаем отрезки а11а12 и а21а22 6. Если отрезки а11а12 и а21а22 невозрастающие, то стратегия В2 доминирует стратегию В1. Если отрезки а11а12 и а21а22 убывающие, то стратегия В2 строго доминирует стратегию В1. 7. Если отрезок а11а12 лежит не ниже отрезка а21а22, то стратегия А1 доминирует стратегию А2. Если отрезок а11а12 лежит не ниже отрезка а21а22, и не пересекается с ним, то стратегия А1 строго доминирует стратегию А2. 8. Находим верхнюю огибающую отрезков а11а12 и а21а22. 9. Находим наинизшие точки верхней огибающей. 10. Проектируем их ортогонально на горизонтальный отрезок [0,1]. 11. Полученные проекции р определяют оптимальные стратегии (Q° = (1 - q°, q°) игрока В. 12. Ордината наинизшей точки верхней огибающей равна цене игры V. 13. Нижний из двух концов верхней огибающей (лежащих на перпендикулярах) есть верхняя цена игры в чистых стратегиях 14. Верхний из двух нижних концов а11а12 и а21а22 есть нижняя цена игры в чистых стратегиях 15. Если элемент является верхним на перпендикуляре, где он лежит, и нижним концом отрезка а11а12 и а21а22, на котором он лежит, то этот элемент является седловой точкой. В этом случае чистая стратегия игрока А, номер которой совпадает с первым индексом седловой точки, является оптимальной.
49. Геометрический метод нахождения оптимальных смешанных стратегий игрока А и цены игры в смешанных стратегиях в игре размерности 1. Берем горизонтальный отрезок [0,1]. 2. В концах отрезка [0,1] проводим к нему 2 перпендикуляра: левый соответ. стратегии А1 и правый, соотв.стратегии А2. 3. На левом перпендикуляре от точки 0 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) элементы первой строки матрицы А 4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] (как на вертикальной числовой оси) элементы второй строки матрицы А 5. Каждую пару точек, изображающих элементы
6. Если все отрезки Если все отрезки 7. Если все отрезки Если все отрезки 8. Если отрезок Если отрезок 9. Находим нижнюю огибающую отрезков 10. На нижней огибающей наивысшую точку (точки). 11. Абсцисса 12. Ордината наивысшей точки нижней огибающей = цене игры V. 13. Верхний из двух концов нижней огибающей (лежащих на перпендикулярах) есть нижняя цена игры в чистых стратегиях 14. Нижний из верхних концов отрезков 15. Если элемент является нижним на перпендикуляре, где он лежит, и верхним концом отрезка на котором он лежит, то этот эл-т является седловой точкой.
50. Формулы для нахождения цены игры в смешанных стратегиях и стратегий игрока А, оптимальных во множестве смешанных стратегий, в игре размерности 2*n Если через наивысшую точку нижней огибающей отрезков a1ja2j, j=1, 2,..., n, порождаемых чистыми стратегиями Bj, j=1, 2,..., n, игрока В, проходят два каких-либо отрезка
и, следовательно,
Тогда оптимальная смешанная стратегия игрока А:
Это были случаи, когда через максимальную точку нижней огибающей проходит более одного отрезка, однако бывает, что через данную точку проходит только один отрезок. При этом, если он параллелен отрезку [0, 1], то максимальные точки заполняют некоторый сплошной промежуток, и множество оптимальных стратегий игрока А:
где 51. Теорема о необходимом и достаточном условии оптимальности смешанной стратегии игрока В в игре размерности 2*n Пусть через максимальную точку N нижней огибающей отрезков a1ja2j, j = 1, 2, …, n, порождаемых чистыми стратегиями Bj, j = 1, 2, …, n, игрока В, проходят два каких-либо отрезка a1j1a2j1 и a1j2a2j2, j1 неравно j2, j1, j2 ϵ {1, 2, …, n}. Для того чтобы смешанная стратегия QO = (
qj = 0, j ϵ {1, 2, …, n} \ {j1, j2}, была оптимальной, необходимо и достаточно, чтобы отрезки a1j1a2j1 и a1j2a2j2 имели разные наклоны.
52. Геометрический метод нахождения цены игры размера 1. Берем горизонтальный отрезок [0,1]. 2. В концах отрезка [0,1] проводим к нему 2 перпендикуляра: левый правый. 3. На левом перпендикуляре от точки 0 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) элементы первого столбца матрицы А 4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] (как на вертикальной числовой оси) элементы второго столбца матрицы А 5. Каждую пару точек, изображающих элементы
6. Если все отрезки Если все отрезки 7. Если все отрезки Если все отрезки 8. Если отрезок Если отрезок 9. Находим верхнюю огибающую отрезов 10. На верхней огибающей находим наинизшую точку (точки). 11. Абсцисса 12. Ордината наинизшей точки высшей огибающей = цене игры V 13. Верхний из нижних концов огибающей (лежащей на перпендикулярах) есть нижняя цена игры в чистых стратегиях 14. Нижний из концов верхней огибающей (лежащий на перпендикулярах) есть верхняя цена игры в чистых стратегиях 15. Если элемент является нижним концом отрезка, на котором лежит, и верхним на перпендикуляре, то этот эл-т является седловой точкой.
59. Теорема об эквивалентности решения матричной игры размерности m*n решению пары двойственных друг другу стандартных задач линейного программирования Рассмотрим игру с m * n -матрицей выигрышей А в которой все элементы положительны. Если матрица содержит неположительные элементы, то ее можно привести к желаемому виду путем аффинного преобразования, при этом цена игры увеличивается на прибавленное число, а опт. стратегии игроков останутся прежними. При применении опт. стратегии игроком А будет получен выигрыш не меньше цены игры V (при любой выбранной игроком В чистой стратегии), т.е.
Разделим полученные неравенства и условия нормировки на V. Введем новые переменные: pi0/V=xi (i=1,..,m). Из условия нормировки p1+..+pm=1 получаем задачу минимизации линейной функции F(x) = x1+…+xm, для увеличения выигрыша игрока А при ограничениях
Используя решение ЗЛП определим цену игрыV= 1/ Для игрока В следует учесть что он, применяя опт. стратегию, стремится проиграть не больше V при любой чистой стратегии игрока А. Новая переменная yi = qi0/V, (j=1,...,n), получаем задачу максимизации F(y) = y1+…+yn для уменьшения проигрыша игрока В. Решение ЗЛП определяет опт стратегию Q0игрока В при цене игры V=1/
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 737; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 и не имеет седловой точки, то чистые стратегии А1, В1 и А2, В2 входят в соответствующие оптимальные смешанные стратегии
и не имеет седловой точки, то чистые стратегии А1, В1 и А2, В2 входят в соответствующие оптимальные смешанные стратегии  соответственно с равными вероятностями:
соответственно с равными вероятностями:  .
. А1, В1 и А2, В2 входят в соответствующие оптимальные смешанные стратегии
А1, В1 и А2, В2 входят в соответствующие оптимальные смешанные стратегии  , и цена игры
, и цена игры (
( .
.
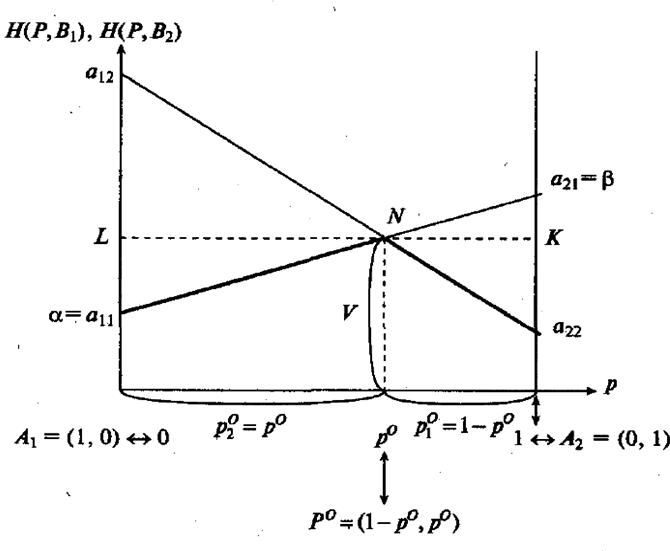 Геометрическое нахождение оптимальных стратегий игрока А, цены гры, нижней и верхней цен игры в чистых стратегиях, седловых точек матрицы игры и доминирующих стратегий игроков можно проводить по следующему алгоритму «А».
Геометрическое нахождение оптимальных стратегий игрока А, цены гры, нижней и верхней цен игры в чистых стратегиях, седловых точек матрицы игры и доминирующих стратегий игроков можно проводить по следующему алгоритму «А».
 .
. .
.
 ,
,  , j=1,2,…n, стоящие в j-м столбце матрицы А, соединяем отрезком
, j=1,2,…n, стоящие в j-м столбце матрицы А, соединяем отрезком  . Таким образом, будут построены nотрезков, представляющих собой графики nлинейных функций
. Таким образом, будут построены nотрезков, представляющих собой графики nлинейных функций
 лежит не ниже отрезка
лежит не ниже отрезка  ,
,  доминирует
доминирует  .
. строго доминирует
строго доминирует 
 этой точки является вероятностью выбора игроком А чистой стратегии А2 в оптимальной смешанной стратегии
этой точки является вероятностью выбора игроком А чистой стратегии А2 в оптимальной смешанной стратегии  ).
). В этом случае чистая стратегия игрока В, номер которой совпадает со вторым индексом седловой точки, является оптимальной.
В этом случае чистая стратегия игрока В, номер которой совпадает со вторым индексом седловой точки, является оптимальной. , j1≠j2, j1, j2
, j1≠j2, j1, j2  , то абсцисса этой наивысшей точки равна:
, то абсцисса этой наивысшей точки равна:

 , а цена игры:
, а цена игры:
 ,
, - абсциссы соответственно крайних максимальных точек нижней огибающей. Это множество
- абсциссы соответственно крайних максимальных точек нижней огибающей. Это множество  выражается отрезком
выражается отрезком 
 игрока В, где
игрока В, где

 и оптимальных смешанных стратегий игрока В
и оптимальных смешанных стратегий игрока В ,
,  , i=1,2,…m, стоящие в i-м столбце матрицы А, соединяем отрезком
, i=1,2,…m, стоящие в i-м столбце матрицы А, соединяем отрезком  . Таким образом, будут построены m отрезков, представляющих собой графики m линейных функций
. Таким образом, будут построены m отрезков, представляющих собой графики m линейных функций
 имеют неотриц наклон, т.е. положительный или нулевой (др.словами, все отрезки
имеют неотриц наклон, т.е. положительный или нулевой (др.словами, все отрезки  , то стратегия
, то стратегия  доминирует стратегию
доминирует стратегию  .
. лежит не ниже отрезка
лежит не ниже отрезка  доминирует
доминирует 
 доминирует
доминирует  этой точки является вероятностью выбора игроком А чистой стратегии B2 в оптимальной смешанной стратегии
этой точки является вероятностью выбора игроком А чистой стратегии B2 в оптимальной смешанной стратегии  ).
).
 В этом случае чистая стратегия игрока А, номер которой совпадает со первым индексом седловой точки, является оптимальной.
В этом случае чистая стратегия игрока А, номер которой совпадает со первым индексом седловой точки, является оптимальной.

 , а из формулы замены – оптимальную смешанную стратегию P0 игрока А.
, а из формулы замены – оптимальную смешанную стратегию P0 игрока А.



