Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип доминирования. Теорема о доминирующих стратегиях и следствия из нееСодержание книги
Поиск на нашем сайте
Один из способов упрощения игр основывается на принципе доминирования, который позволяет в некоторых случаях игру с матрицей А свести к эквивалентной игре с матрицей меньшего размера. Между множеством
строк (
из которого ясно, что, в частности, каждой чистой стратегии Если для двух выпуклых комбинаций строк матрицы А
и
выполняются неравенства
то говорят, что строка (2) доминирует строку (1), а строка (1) доминирует строкой (2). Если каждое неравенство (3) является равенством, то строки (1) и (2) называют дублирующими. Если же каждое неравенство (3) является строгим, то говорят, что строка (2) строго доминирует строку (1), а строка (1) строго доминируется строкой (2). Аналогичная терминология используется и для соответствующих стратегий игрока А. А именно, если строка (2) доминирует, соответственно дублирует, соответственно строго доминирует строку (1), то говорят, что стратегия
Между смешанными (в том числе и чистыми) стратегиями
столбцов проигрышей Н(
из которого видно, что, в частности, каждой чистой стратегии Если для двух выпуклых комбинаций столбцов матрицы А
и
выполняются неравенства
то говорят, что столбец (4) (стратегия Теорема. Справедливы следующие предложения: 1. Если k-ая строка (k ϵ {1, 2, …, m}) матрицы А игры доминируется некоторой выпуклой комбинацией остальных ее строк, то существует оптимальная смешанная стратегия Рk = ( 2. Если k-ая строка (k ϵ {1, 2, …, m}) матрицы А игры строго доминируется некоторой выпуклой комбинацией остальных ее строк, то относительно любой оптимальной смешанной стратегии РО = 3. Если l-ый столбец (l ϵ {1, 2, …, n}) матрицы А игры доминируется некоторой выпуклой комбинацией остальных ее столбцов, то существует оптимальная смешанная стратегия Ql = 4. Если l-ый столбец (l ϵ {1, 2, …, n}) матрицы А игры строго доминируется некоторой выпуклой комбинацией остальных ее столбцов, относительно любой оптимальной смешанной стратегии QО = Следствие 1: 1. Если k-я строка матрицы игры доминируется некоторой другой строкой, то существует оптимальная смешанная стратегия игрока А, относительно которой чистая стратегия Аk является пассивной, т.е. входит в эту смешанную стратегию с нулевой вероятностью. 2. Если k-я строка матрицы игры строго доминируется некоторой другой строкой, то относительно любой оптимальной смешанной стратегии игрока А чистая стратегия Аk является пассивной, т.е. входит в любую оптимальную смешанную стратегию с нулевой вероятностью. 3. Если l-ый столбец матрицы игры доминируется некоторым другим столбцом, то существует оптимальная смешанная стратегия игрока В, относительно которой чистая стратегия Вl является пассивной, т.е. входит в эту смешанную стратегию с нулевой вероятностью. 4. Если l-ый столбец матрицы игры строго доминируется некоторым другим столбцом, то относительно любой оптимальной смешанной стратегии игрока В чистая стратегия Вl является пассивной, т.е. входит в любую оптимальную смешанную стратегию с нулевой вероятностью. Следствие 2: Одну из двух дублирующих чистых стратегий можно удалить.
41. Критерий седловой точки платежной матрицы игры размера Теорема: Пусть i, k – номера строк, а j, l – номера столбцов. И пусть матрица А размером 2х2. Для того, чтобы элемент aij был седловой точкой матрицы, необходимо и достаточно выполнение хотя бы одного из следующих условий: 1. Либо можно удалить k-ю строку, как доминируемую i-й строкой, и уже в i-й строке удалить l-й столбец, потому что им доминирует j-й. 2. Либо можно начать со столбцов, удалить там один из доминируемых (например j-й), а потом в оставшемся l-м столбце удалить одну из строк. Если в матрице нет доминируемых строк и столбцов – значит, нет седловых точек. (можно не писать: Другими словами, для того, чтобы у матрицы А размером 2*2 не существовало седловой точки, необходимо и достаточно, чтобы среди строк и среди столбцов не было доминируемых (в частности, дублируемых).) 42. Критерий существования седловой точки в игре размера Теорема: Для того чтобы в игре с матрицей А размером 2*2 существовала седловая точка, необходимо и достаточно существование смешанной стратегии, относительно которой одна из чистых стратегий является пассивной. Другими словами, для того чтобы в игре с матрицей 2*2 существовала седловая точка, необходимо и достаточно существование чистой оптимальной стратегии. Док-во: 1) Необходимость. Пусть 2) Достаточность. Пусть стратегия Пусть Если Если Наконец, рассмотрим случай Рассмотрим возможность Рассмотрим возможность
43. Признак (достаточное условие) существования седловой точки платежной матрицы размерности 2*2 Теорема: Для того чтобы у матрицы А размером 2*2 существовала седловая точка, достаточно, чтобы сумма элементов главной диагонали матрицы А равнялась сумме элементов ее побочной диагонали: Доказательство: из неравенства:
Тогда из неравенства: 2. Тогда из нер-ва: 44. Формулы для нахождения оптимальных смешанных стратегий игрока А и цены игры размерности 2*2 без седловой точки Теорема. Пусть матрица А размером 2*2 не имеет седловой точки. Тогда каждый из игроков А и В обладает единственной оптимальной смешанной стратегией соответственно
Цена игры в смешанных стратегиях
45. Формулы для нахождения оптимальных смешанных стратегий игрока В и цены игры размерности 2*2 без седловой точки Теорема. Пусть матрица А размером 2*2 не имеет седловой точки. Тогда каждый из игроков А и В обладает единственной оптимальной смешанной стратегией соответственно
Цена игры в смешанных стратегиях
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1076; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.146.180 (0.008 с.) |

 смешанных (в том числе и чистых) стратегий
смешанных (в том числе и чистых) стратегий  игрока А и выпуклыми комбинациями
игрока А и выпуклыми комбинациями
 матрицы А, представляющими собой строки
матрицы А, представляющими собой строки  выигрышей
выигрышей 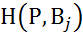 , j=1,2,…,n, игрока А в ситуациях
, j=1,2,…,n, игрока А в ситуациях  , j=1,2,…,n, устанавливается взаимно-однозначное соответствие
, j=1,2,…,n, устанавливается взаимно-однозначное соответствие
 игрока А ставится во взаимно-однозначное соответствие k-я строка
игрока А ставится во взаимно-однозначное соответствие k-я строка  матрицы А.
матрицы А.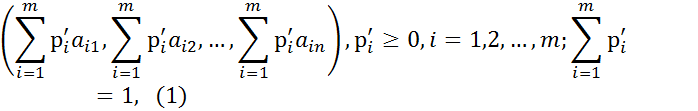


 доминирует, соответственно дублирует, соответственно строго доминирует стратегию
доминирует, соответственно дублирует, соответственно строго доминирует стратегию 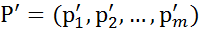 .
. игрока В и выпуклыми комбинациями
игрока В и выпуклыми комбинациями T,
T, 
 T , j=1,2,…,n, матрицы А (Т- значок транспонирования), представляющими собой столбцы
T , j=1,2,…,n, матрицы А (Т- значок транспонирования), представляющими собой столбцы  T
T , i=1,2,…,m, игрока В в ситуациях (
, i=1,2,…,m, игрока В в ситуациях ( T ,
T , , l =1,2,…,n, игрока В ставится во взаимно-однозначное соответствие l -й столбец
, l =1,2,…,n, игрока В ставится во взаимно-однозначное соответствие l -й столбец  T матрицы А.
T матрицы А. T
T 
 T
T 

 доминирует столбец (5) (стратегию
доминирует столбец (5) (стратегию  , а столбец (5) (стратегия
, а столбец (5) (стратегия  ) доминируется столбцом (4) (стратегией
) доминируется столбцом (4) (стратегией 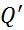 ). Если каждое неравенство (6) является равенством, то столбцы (4) и (5) (стратегии
). Если каждое неравенство (6) является равенством, то столбцы (4) и (5) (стратегии  игрока А, относительно которой k-я чистая стратегия Аk является пассивной, т.е. входит в смешанную стратегию Рk с нулевой вероятностью:
игрока А, относительно которой k-я чистая стратегия Аk является пассивной, т.е. входит в смешанную стратегию Рk с нулевой вероятностью:  =0
=0 игрока А, чистая k-я стратегия является пассивной, т.е. входит в стратегию РО с нулевой вероятностью:
игрока А, чистая k-я стратегия является пассивной, т.е. входит в стратегию РО с нулевой вероятностью:  =0
=0 игрока В, относительно которой l-я чистая стратегия Bl является пассивной, т.е. входит в стратегию Ql с нулевой вероятностью:
игрока В, относительно которой l-я чистая стратегия Bl является пассивной, т.е. входит в стратегию Ql с нулевой вероятностью:  =0
=0 игрока В чистая l-я стратегия Bl является пассивной, т.е. входит в стратегию Q0 с нулевой вероятностью:
игрока В чистая l-я стратегия Bl является пассивной, т.е. входит в стратегию Q0 с нулевой вероятностью:  =0
=0 , в терминах доминирования
, в терминах доминирования в терминах пассивных стратегий
в терминах пассивных стратегий , - номера чистых стратегий игрока А, а
, - номера чистых стратегий игрока А, а  , номера чистых стратегий игрока В. Пусть
, номера чистых стратегий игрока В. Пусть  - седловая точка. Тогда
- седловая точка. Тогда  - оптимальная стратегия игрока А. Так как чистую оптимальную стратегию
- оптимальная стратегия игрока А. Так как чистую оптимальную стратегию 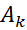 - с нулевой вероятностью, то стратегия
- с нулевой вероятностью, то стратегия  , в которую чистая стратегия
, в которую чистая стратегия  входит с вероятностью, равной 1. Это означает, что
входит с вероятностью, равной 1. Это означает, что  , т.е.
, т.е.  - некоторая оптимальная стратегия игрока В, в которую чистые стратегии
- некоторая оптимальная стратегия игрока В, в которую чистые стратегии 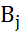 и
и  входят соответственно с вероятностями
входят соответственно с вероятностями  и
и  . Так как
. Так как 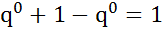 , то хотя бы одно из чисел
, то хотя бы одно из чисел  , то чистая стратегия
, то чистая стратегия  . В то же время стратегия
. В то же время стратегия  , а
, а  следует, что
следует, что  - седловая точка.
- седловая точка. , то чистая стратегия
, то чистая стратегия 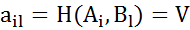 , которое имеет место в силу теоремы об активных стратегиях, следует, что
, которое имеет место в силу теоремы об активных стратегиях, следует, что  и
и  . В этом случае стратегии
. В этом случае стратегии 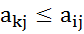 и
и 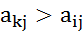 .
.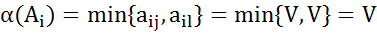 . Из
. Из 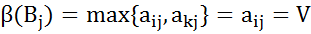 . В итоге получаем двойное равенство
. В итоге получаем двойное равенство  , которое означает, что
, которое означает, что 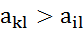 , то это неравенство вместе с
, то это неравенство вместе с  , то элемент
, то элемент  - наименьший в i-й строке и наибольший в -м столбеце, т.е.
- наименьший в i-й строке и наибольший в -м столбеце, т.е. 
 возможны случаи:
возможны случаи:
 , которое вместе с
, которое вместе с  означает, что второй столбец матрицы А доминируется ее первым столбцом. Тогда на основании следствия из теоремы (Если l-й столбец матрицы игры доминируется некоторым другим столбцом, то существует оптимальная смешанная стратегия игрока В) существует оптимальная смешанная стратегия игрока в, в которую чистая стратегия В2 входит с нулевой вероятностью, то есть В1 является оптимальной. Следовательно стратегия В2 пассивна и по теореме о существовании седловой точки в игре размера 2*2 в терминах пассивных стратегий: ( для того чтобы в игре с матрицей А размером 2*2 существовала седловая точка, необходимо и достаточно существование смешанной стратегии, относительно которой одна из чистых стратегий явл пассивной)у матрицы А существует седловая т.
означает, что второй столбец матрицы А доминируется ее первым столбцом. Тогда на основании следствия из теоремы (Если l-й столбец матрицы игры доминируется некоторым другим столбцом, то существует оптимальная смешанная стратегия игрока В) существует оптимальная смешанная стратегия игрока в, в которую чистая стратегия В2 входит с нулевой вероятностью, то есть В1 является оптимальной. Следовательно стратегия В2 пассивна и по теореме о существовании седловой точки в игре размера 2*2 в терминах пассивных стратегий: ( для того чтобы в игре с матрицей А размером 2*2 существовала седловая точка, необходимо и достаточно существование смешанной стратегии, относительно которой одна из чистых стратегий явл пассивной)у матрицы А существует седловая т.
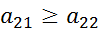 , которое вместе с
, которое вместе с  означает строгую доминируемость первого столбца матрицы А ее вторым столбцом. А потому на основании следствия 2 теоремы 11.1 стратегия В1 является пассивной и, => по теореме (той же, что и в 1-м пункте) у матрицы А существует седловая точка.
означает строгую доминируемость первого столбца матрицы А ее вторым столбцом. А потому на основании следствия 2 теоремы 11.1 стратегия В1 является пассивной и, => по теореме (той же, что и в 1-м пункте) у матрицы А существует седловая точка. , где:
, где: