
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выигрыш-функция в смешанных стратегиях и различные формулы ее представления (Координатная формула. Векторно-матричные формулы выигрыш-функции в смешанных стратегиях)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Функция выигрыша игрока 𝐴 в смешанных стратегиях – функция 𝐻, определенная на декартовом произведении 𝑆𝐴× 𝑆𝐵 множеств смешанных стратегий соответственно игроков 𝐴 и 𝐵, и ставящая в соответствие каждой ситуации (𝑃, 𝑄) ∈ 𝑆𝐴× 𝑆𝐵 в смешанных стратегиях средний выигрыш игрока 𝐴 в этой ситуации, определяемый следующим образом: 𝐻(𝑃,𝑄) = ∑𝑚𝑖=1 ∑𝑛𝑗=1 𝑝𝑖𝑎𝑖𝑗𝑞𝑗, где 𝑃 = (𝑝1,...,𝑝𝑚), 𝑄 = (𝑞1,...,𝑞𝑛) (1) Так как Если 𝑃 = (𝑝1 = 0,...,𝑝𝑖−1 =0,𝑝𝑖=1,𝑝𝑖+1 =0,...,𝑝𝑚=0)=𝐴𝑖, 𝑄=(𝑞1 =0,...,𝑞𝑗−1 =,𝑞𝑗=1,𝑞𝑗+1 =0,...,𝑞𝑛=0)=𝐵𝑗 т.е. (𝑃,𝑄) = (𝐴𝑖,𝐵𝑗) ∈ 𝑆𝐴𝐶×𝑆𝐵𝐶, то из (1) следует, что: 𝐻(𝑃,𝑄)=𝐻(𝐴𝑖,𝐵𝑗)=𝑎𝑖𝑗=𝐹(𝐴𝑖,𝐵𝑗)=𝐹(𝑃,𝑄). Данное равенство означает, что функция выигрыша в смешанных стратегиях Н совпадает на декартовом произведении 𝑆𝐴𝐶× 𝑆𝐵𝐶с функцией выигрыша в чистых стратегиях 𝐹 и, следовательно, является ее расширением (продолжением) с декартова произведения 𝑆𝐴𝐶× 𝑆𝐵𝐶на декартово произведение 𝑆𝐴× 𝑆𝐵. Форма 𝐻(𝑃,𝑄) = ∑𝑚𝑖=1 ∑𝑛𝑗=1 𝑝𝑖𝑎𝑖𝑗𝑞𝑗, (𝑃, 𝑄) ∈𝑆𝐴× 𝑆𝐵задания функции выигрыша в смешанных стратегиях называется координатной. Функцию Н можно задать и в матричной форме
где 𝑃 = (𝑝1,...,𝑝𝑚) –вектор-строка размера 1*m
- матрица игры (матрица выигрышей игрока А в чистых стратегиях) размера m*n
- вектор-столбец размера n*1 Подчеркнем, что размеры матриц – множители в правой части (1) – удовлетворяют условиям возможности перемножения этих матриц, т.е. для двух соседних множителей число столбцов левого равно числу строк правого. Показатель эффективности смешанной стратегии игрока А относительно множества смешанных стратегий игрока В и его существование Для каждой смешанной стратегии
Число Доказательство: Если зафиксировать произвольную смешанную стратегию
Показатель неэффективности смешанной стратегии игрока В относительно множества смешанных стратегий игрока А и его существование Для каждой смешанной стратегии
Число Доказательство: Если зафиксировать произвольную смешанную стратегию
Показатель эффективности смешанной стратегии игрока А относительно множества чистых стратегий игрока В. соотношение между показателями эффективности смешанной стратегии игрока А относительно множеств смешанных и чистых стратегий игрока В
Число
называется показателем эффективности смешанной стратегии Теорема. Показатели эффективности любой смешанной (в частности, чистой) стратегии
Доказательство. Так как И, следовательно
Докажем противоположное неравенство. Пусть
Тогда используя формулы
Для любых
Последнее неравенство и
противоположны, следовательно Показатель неэффективности смешанной стратегии игрока В относительно множества чистых стратегий игрока В. Соотношение между показателями неэффективности смешанной стратегии игрока В относительно множеств смешанных и чистых стратегий игрока А
Число
называется показателем неэффективности смешанной стратегии Q игрока B относительно множества Теорема. Показатели неэффективности любой смешанной (в частности, чистой) стратегии
Доказательство. Так как И, следовательно
Докажем противоположное неравенство. Пусть Тогда используя формулы
Для любых
Последнее неравенство и
противоположны, следовательно
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.009 с.) |

 и, следовательно,
и, следовательно, 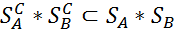 , то декартово произведение
, то декартово произведение 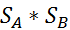 множеств смешанных стратегий игроков А и В является расширение декартова произведения
множеств смешанных стратегий игроков А и В является расширение декартова произведения  множеств чистых стратегий игроков А и В.
множеств чистых стратегий игроков А и В.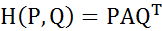 (1)
(1)

 игрока А существует
игрока А существует
 называется показателем эффективности смешанной стратегии
называется показателем эффективности смешанной стратегии 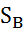 смешанных стратегий игрока В
смешанных стратегий игрока В будет функцией одного векторного аргумента Q, определенного на симплексе
будет функцией одного векторного аргумента Q, определенного на симплексе  функции
функции  которое является компактом, а непрерывная на компакте функция достигает своей нижней и верхней граней. Поэтому для любого
которое является компактом, а непрерывная на компакте функция достигает своей нижней и верхней граней. Поэтому для любого  , т.е. для любого
, т.е. для любого  такая, что
такая, что 
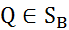 игрока B существует
игрока B существует
 называется показателем неэффективности смешанной стратегии
называется показателем неэффективности смешанной стратегии  смешанных стратегий игрока A.
смешанных стратегий игрока A. видно, что она непрерывна по аргументу P на множестве
видно, что она непрерывна по аргументу P на множестве  которое является компактом, а непрерывная на компакте функция достигает своей нижней и верхней граней. Поэтому для любого
которое является компактом, а непрерывная на компакте функция достигает своей нижней и верхней граней. Поэтому для любого  , т.е. для любого
, т.е. для любого  такая, что
такая, что

 чистых стратегий игрока В. В частности, если
чистых стратегий игрока В. В частности, если  – чистая стратегия, то
– чистая стратегия, то  - показатель эффективности чистой стратегии
- показатель эффективности чистой стратегии  (относительно множества
(относительно множества 
 то
то 

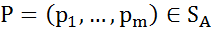 и
и
 и
и  и
и  , получим неравенство
, получим неравенство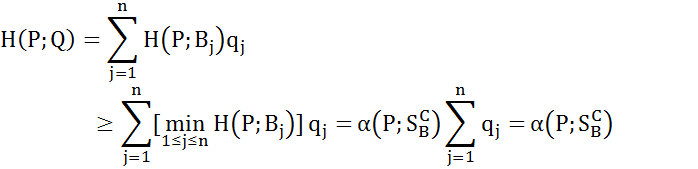



 чистых стратегий игрока A. В частности, если
чистых стратегий игрока A. В частности, если  – чистая стратегия, то
– чистая стратегия, то  - показатель неэффективности чистой стратегии
- показатель неэффективности чистой стратегии 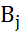 (относительно множества
(относительно множества 
 то
то 

 и
и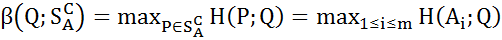 и
и  , получим неравенство
, получим неравенство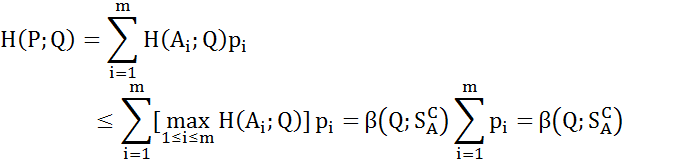
 будем иметь
будем иметь




