
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Верхняя и нижняя цены игры при использовании смешанных стратегийСодержание книги
Поиск на нашем сайте
Пусть Предположим, что первый игрок применяет смешанную стратегию Обозначим гарантированное значение выигрыша первого игрока при стратегии p через A(p):
Далее первого игрока будет интересовать выбор из всех возможных стратегий
Стратегия Для второго игрока рассуждения аналогичные. Применяя свою смешанную стратегию
Далее второго игрока будет интересовать выбор из всех возможных стратегий
Стратегия Таким образом, Теорема. Если имеется игра a) b) c) d) e) Условие «а» говорит о том, что при выборе первым игроком любой смешанной стратегии значение его гарантированного выигрыша равно значению гарантированного выигрыша при использовании вторым игроком только чистых стратегий. Согласно условию «b» нижняя цена игры при смешанных стратегиях первого игрока не меньше нижней цены игры при чистых стратегиях, т.е. что существует смешанная стратегия, которая во всяком случае не хуже оптимальной чистой стратегии. Пункты «c»и «d» содержат аналогичные утверждения в отношении второго игрока. Пункт «e» означает, что нижняя цена игры Доказательство – Коршунов Ю.М. Математические основы кибернетики. Следствие. Из этого следует, что если игра Г имеет цену, т.е. Но игра G была введена для анализа таких игр, у которых Теорема о том, что всякая конечная игра имеет цену, и у каждого из игроков имеются оптимальные стратегии, является основной теоремой теории игр.
Основная теорема антагонистических игр. S-игра
Играм, в которых у первого игрока конечное число стратегий, можно дать полезную геометрическую интерпретацию. Пусть задана игра Можно рассмотреть множество векторов:
Игра, заданная множеством точек Правила S-игры следующие: второй игрок выбирает одну из точек
Нетрудно видеть, что S-игра эквивалентна обычной игре в нормальной форме Если число стратегий первого игрока равно двум, то S-игра имеет наглядное геометрическое интерпретацию, т.к. точки множества
Пример: Рассмотрим игру
Обозначим через Теорема. Любая смешанная стратегия второго игрока может быть представлена точкой, принадлежащей выпуклой оболочке Доказательство. Рассмотрим смешанные стратеги игроков
Обозначим через S точку в m-мерном пространстве с координатами
………………………….
Учитывая, что
Видим, что S есть не что иное, как средневзвешенное точек Справедливо и обратное. Так как любая точка S, принадлежащая выпуклой оболочке
Следствие. Поскольку смешанная стратегия первого игрока остается в S-игре той же самой, что и в обычной игре, из доказанной теоремы следует, что S – игра полностью эквивалентна обычной игре, т.е. любая игра может быть представлена в виде эквивалентной S-игры.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 183; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.239.63 (0.007 с.) |

 — игра, а
— игра, а 
 — ее смешанное расширение.
— ее смешанное расширение. . Этого игрока интересует, каков будет его гарантированный выигрыш, т.е. та наименьшая сумма выигрыша, которую он может наверняка себе обеспечить, даже если второй игрок применяет свою наилучшую смешанную стратегию
. Этого игрока интересует, каков будет его гарантированный выигрыш, т.е. та наименьшая сумма выигрыша, которую он может наверняка себе обеспечить, даже если второй игрок применяет свою наилучшую смешанную стратегию  .
. .
. .
.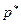 называется максиминной стратегией первого игрока в смешанном расширении игры.
называется максиминной стратегией первого игрока в смешанном расширении игры. , его максимальный проигрыш будет равен:
, его максимальный проигрыш будет равен: .
. .
. является минимаксной стратегией второго игрока в смешанном расширении игры.
является минимаксной стратегией второго игрока в смешанном расширении игры. называется нижней ценой игры в смешанном расширении, а
называется нижней ценой игры в смешанном расширении, а  называется верхней ценой игры в смешанном расширении.
называется верхней ценой игры в смешанном расширении. ;
; ;
; ;
;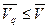 ;
; .
. при использовании смешанных стратегий не превосходит верхней цены игры
при использовании смешанных стратегий не превосходит верхней цены игры  , т.е. при использовании наилучших смешанных стратегий гарантированный выигрыш первого игрока не превзойдет обеспеченного проигрыша второго игрока.
, т.е. при использовании наилучших смешанных стратегий гарантированный выигрыш первого игрока не превзойдет обеспеченного проигрыша второго игрока. .
. (это имеет место для игр с седловой точкой), то
(это имеет место для игр с седловой точкой), то  , т.е. игра G также имеет цену. Поэтому оптимальная стратегия в игре Г является оптимальной и в игре G. В этом случае игру G можно не рассматривать, а оптимальные стратегии игроков находить методом, описанным для игр с седловой точкой.
, т.е. игра G также имеет цену. Поэтому оптимальная стратегия в игре Г является оптимальной и в игре G. В этом случае игру G можно не рассматривать, а оптимальные стратегии игроков находить методом, описанным для игр с седловой точкой. . Применение смешанных стратегий позволяет найти цену игры и оптимальные стратегии игроков в этом случае.
. Применение смешанных стратегий позволяет найти цену игры и оптимальные стратегии игроков в этом случае. .
.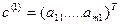 …..
…..  .
. , получила название S-игры.
, получила название S-игры. , а первый игрок выбирает i-ую координату этой точки
, а первый игрок выбирает i-ую координату этой точки  . При этом выигрыш первого игрока, соответственно проигрыш второго, будет равен значению i-ой координаты точки
. При этом выигрыш первого игрока, соответственно проигрыш второго, будет равен значению i-ой координаты точки  , т.е.
, т.е.  :
: .
. , а выбор координаты этой точки эквивалентен выбору стратегии
, а выбор координаты этой точки эквивалентен выбору стратегии  .
. , в которой столбцы определяют точки
, в которой столбцы определяют точки  с координатами
с координатами  ).
).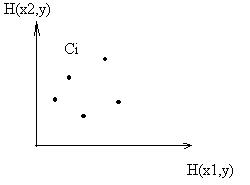
 . Эквивалентная S - игра содержит 5 точек:
. Эквивалентная S - игра содержит 5 точек:  ,
,  ,
,  ,
,  ,
,  . Геометрическое изображение этой игры приведено на рисунке.
. Геометрическое изображение этой игры приведено на рисунке.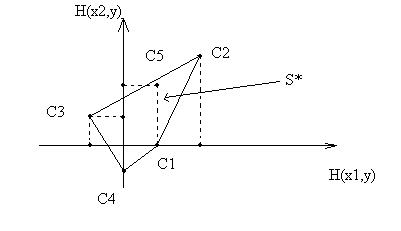
 выпуклую оболочку конечного множества точек
выпуклую оболочку конечного множества точек  может рассматриваться как некоторая смешанная стратегия второго игрока.
может рассматриваться как некоторая смешанная стратегия второго игрока. и
и  . При использовании этих смешанных стратегий проигрыш второго игрока
. При использовании этих смешанных стратегий проигрыш второго игрока , где
, где  .
. :
: ;
; .
.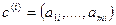 , это выражение можно записать в виде векторного соотношения
, это выражение можно записать в виде векторного соотношения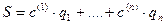 .
. с весами
с весами 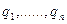 , а следовательно, S есть некоторая точка, принадлежащая выпуклой оболочке
, а следовательно, S есть некоторая точка, принадлежащая выпуклой оболочке 


