
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Строго выпуклые игры на единичном квадратеСодержание книги
Поиск на нашем сайте
Функция φ(x) называется выпуклой, если для любых двух точек z1 и z2 из множества Z выполняется неравенство: φ(λz1 + (1-λ)z2 ) Если неравенство строгое, то и функция строго выпуклая (если неравенство выполняется строго, то вторая производная φ˝(z)>0). Опр. Игра Г=<X,Y,a> называется игрой на единичном квадрате, если X=[0,1] и Y=[0,1], а целевая функция a(x,y) определена для каждой точки этого квадрата. Опр. Игра Г на единичном квадрате называется непрерывной, если функция платежей a(x,y) непрерывна в каждой точке единичного квадрата по обеим переменным. Опр. Непрерывная антагонистическая игра на единичном квадрате называется выпуклой, если функция a(x,y) строго выпукла по Y для всех x a(x, λy1 + (1-λ)y2) < λ a(x,y1) + (1- λ) a(x,y2), Исходя из свойств строгой выпуклости, Теорема. В строго выпуклой игре на единичном квадрате 2-ой игрок имеет единственную оптимальную стратегию, которая является чистой. Цена игры в этом случае v(a), где v(a) — функция платежей. v(a) = Х* — множество стратегий 1-го игрока, состоящее из тех х* х* — тоже чистые стратегии, они называются существенными стратегиями, а остальные – несущественными. Нахождение существенных стратегий 1-ого игрока основано на выполнении следующих свойств. 1. Если y*=1, то у 1-го игрока существует стратегия х1, для которой
Геометрическое истолкование:
При уменьшении y a(x,y) возрастает.
2. Если y*=0, то среди стратегий 1-го игрока существует такая стратегия х2, что
3. Если имеется значение стратегии 0<y*<1, то у 1-го игрока найдутся 2 существенные стратегии х1 и х2,для которых имеет место условие
Наиболее оптимальной стратегией 1-ого игрока является вероятностная смесь стратегий х1 и х2, причем х1 — с вероятностью р, х2 — с вероятностью (1-р).
Доказывается, что решение этого уравнения единственно и принадлежит интервалу
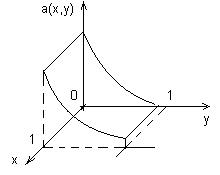
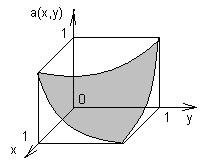
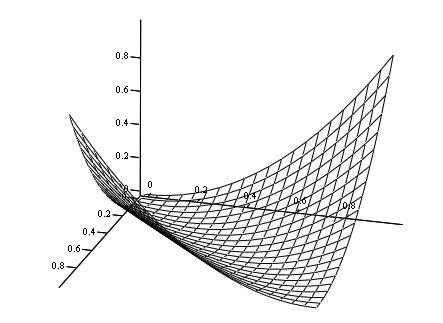
Пример. Пусть имеется игра Г=<X,Y,a>, x,y 1). Рисуем график функции платежей (выигрыша):
2). Проверим функцию платежей на выпуклость.
Функция платежей строго выпукла по у. Имеем дело со строго выпуклой игрой на единичном квадрате.
Найдем v=v(a). Для этого рассмотрим функцию:
Построим таблицу:
y*=0.5 v(a)=0.25 Отсюда видим, что в нашем случае 0<y*<1, а следовательно, у 1-го игрока есть две существенные стратегии: х1 и х2. Для их нахождения рассмотрим зависимость v(a)=a(x,y*)=(x-y*)2=(x-0.5)2=0.25 x1=0, x2=1 — две существенных чистых стратегии 1-го игрока. Проверим, что эти решения действительно являются существенными стратегиями (проверка на противоположность производных).
следовательно, оптимальная стратегия 1-го игрока есть вероятностная смесь по стратегиям х=х1 и х=х2. Найдем эти вероятности.
Покажем, что найденное решение является точкой равновесия. Рассмотрим проигрыши 2-ого игрока при оптимальной стратегии 1-ого: a(x*,y) = p*(x1 - y)2 + (1-p*)(x2 - y)2 = 1/2(-y)2 + 1/2(1-y)2 a(x,y*) — выигрыш 1-ого игрока при условии, что 2-ой примет свою оптимальную чистую стратегию.
Неантагонистические игры N={1,2,…,N} — число игроков (больше двух). Возможны следующие ситуации: 1) совместные действия игроков (коалиции) запрещены по условиям игры, и тогда игра называется бескоалиционной; 2) совместные действия не запрещены, игроки могут образовывать коалиции и действовать совместно. Такие игры называются кооперативными.
Бескоалиционные игры В таких играх каждый игрок действует самостоятельно. Игра Г=<N, {xi}, i Каждый игрок выбирает некоторую стратегию из множества Хi: i Это описание бескоалиционной игры в нормальной форме. Игроки выбирают свои стратегии xi независимо друг от друга. Если для каждого игрока множество стратегий xi конечно, то получаем конечную бескоалиционную игру. Если хотя бы один из игроков имеет бесконечное число стратегий, то это бесконечная бескоалиционная игра. Простейшей бескоалиционной игрой является игра двух лиц. Они могут не только выигрывать или проигрывать, но и делать это совместно (одновременно выигрывать или проигрывать). Опишем такую игру (бескоалиционную) в нормальной форме: Г=<x1,x2,H1,H2>, где {x1,x2}-множество стратегий, H1,H2— функции выигрыша. (x(1),x(2)) Ясно, что если игра конечна, то матрицу Н можно рассмотреть как H1=(aij) m*n A H2=(bij) m*n B Такую игру называют биматричной: Г=<A,B>; aij= -bij,
Библиографический список
1. Петросян Л.А., Зенкевич Н.А., Семина Е.Н. Теория игр.-М.: В.Ш. 1998. 2. Коршунов Ю.М. Математические основы кибернетики. –М.: Энергоатом- издат, 1987. 3. Интрилигатор М. Математические методы оптимизации и математическая теория.- М.: Прогресс, 1975. 4. Карлин С. Математические методы в теории игр, программировании и экономике.- М. Мир.1964. 5. Дюбин Г.Н., Суздаль В.Г. Введение в прикладную теорию игр.- М.: Наука, 1984. 6. Нейман Д., Моргенштерн О. Теория игр и экономическое поведение. М.: Наука, 1970. 7. Гегечкори Е.Т. Математические модели принятия решений в экономике и технике.- Омск, Изд-во ОмГТУ, 2004. 8. Адамчук А.С. и др. Математические модели и игры в экономике: Уч. Пособие, Ставрополь: Сервисшкола, 2004.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.43.98 (0.005 с.) |

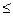 λφ(z1) + (1- λ)φ(z2),
λφ(z1) + (1- λ)φ(z2), 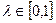
 X. Иными словами, для функции платежей в строго выпуклой игре имеет место неравенство:
X. Иными словами, для функции платежей в строго выпуклой игре имеет место неравенство: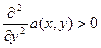
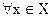 .
.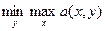 =
= 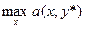 , где y* — оптимальная чистая стратегия 2-го игрока.
, где y* — оптимальная чистая стратегия 2-го игрока. .
.
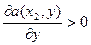 , y=y*.
, y=y*.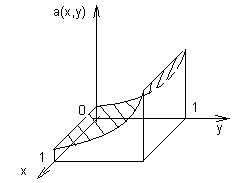
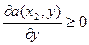 , y=y*
, y=y*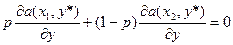 — уравнение, позволяющее определить р.
— уравнение, позволяющее определить р.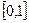 .
.
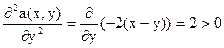
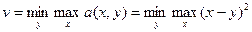
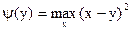 .
.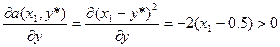
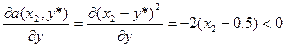
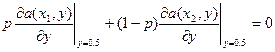
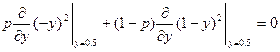
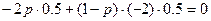
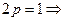 p=0.5
p=0.5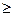
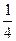 ,
,  y, следовательно минимум 1/4.
y, следовательно минимум 1/4.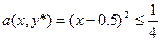
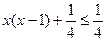
 x(i)
x(i)  ,
,  , следовательно, игра антагонистическая.
, следовательно, игра антагонистическая.


