
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание игры в развернутой формеСодержание книги Поиск на нашем сайте
Основные понятия теории игр Теория игр представляет собой интенсивно развивающуюся математическую дисциплину, являющуюся одним из разделов теории принятия решений (исследования операций). Предметом исследования теории игр являются методы принятия решений в конфликтных ситуациях. Ситуация называется конфликтной, если в ней сталкиваются интересы нескольких лиц, преследующих противоположные цели. Каждая из сторон может проводить ряд мероприятий для достижения своих целей, причем успех одной стороны означает неудачу другой. Авторы первого фундаментального трактата по теории игр Дж. фон Нейман и О. Моргенштерн ориентировались на анализ конфликтных ситуаций в вопросах экономики, когда при наличии свободной конкуренции в роли борющихся сторон выступают торговые фирмы, промышленные предприятия и т.д. Однако конфликтные ситуации встречаются и во многих других областях. К конфликтным ситуациям относятся почти все ситуации, возникающие при планировании военных операций, выборе системы оружия, охране объектов от нападения, преследовании и перехвате цели и т.п. Интересными примерами конфликтных ситуаций являются спортивные состязания, арбитражные споры, аукционы, выборы в парламент при наличии нескольких кандидатов на одно место. То есть областью применения методов теории игр являются: 1) математика; 2) экономика; 3) военная стратегия и тактика; 4) политика. Приведенные примеры показывают большое разнообразие встречающихся на практике конфликтных ситуаций. Обычно эти ситуации трудны для непосредственного анализа из-за множества второстепенных факторов. Для того, чтобы сделать возможным математический анализ конфликтной ситуации, ее необходимо упростить, учтя только основные факторы. Упрощенную формализованную модель конфликтной ситуации называют игрой, а конфликтующие стороны — игроками или лицами, принимающими решения (если это часть теории принятия решения). Следует различать понятие игры и понятие индивидуальной партии этой игры. Игра представляет собой совокупность правил, описывающих поведение игроков и известных всем игрокам. Каждый случай разыгрывания игры некоторым конкретным образом от начала и до конца представляет собой партию игры. Элементами игры являются ходы. Правила игры предусматривают, какова должна быть последовательность ходов, и указывают характер каждого хода. Также правила регламентируют, какие ходы может осуществлять каждый игрок, какие ситуации могут возникнуть, каков будет выигрыш каждого игрока в каждой из ситуаций. Ход — момент игры, связанный с выбором игроком определенной стратегии поведения (определенного образа действий). Ходы бывают личные и случайные. Личный ход представляет собой выбор игроком одного из заданного множества вариантов. Например, каждый ход в шахматах является личным, причем первый ход — выбор из 20 вариантов. Решение, принятое игроком при личном ходе, называют выбором. Случайный ход также представляет собой выбор одного из множества вариантов, но здесь вариант выбирается не игроком, а некоторым механизмом случайного выбора. Примерами случайных ходов может быть сдача карт или бросание монеты. Выбор, осуществляемый при случайном ходе, называют исходом этого хода. Таким образом, партия — законченная совокупность ходов, после которой можно говорить о выигрыше или проигрыше игроков в данной партии. В общем случае, игру можно рассматривать как бесконечную последовательность партий. Стратегия — набор правил, сформулированных до начала игры.
Классификация игр Классификацию игр проводят по различным признакам: 1) по числу игроков; 2) по числу стратегий; 3) по свойствам платежной функции; 4) по характеру предварительной договоренности между игроками. Игру, в которой участвует n игроков, называют игрой с n участниками. Количество участников может быть равным 2, 3 и т.д. При наличии двух игроков могут возникать конфликтные ситуации, и необходимость в координированных действиях (кооперация). Если в игре участвуют три игрока и более, то могут создаваться коалиции, т.е. группы из двух игроков и более, имеющих общую цель и координирующих свои стратегии. По количеству стратегий различают игры конечные и бесконечные. Если хотя бы из игроков располагает бесконечным множеством стратегий, то игру называют бесконечной. Если же каждый из игроков располагает конечным множеством стратегий, то игру называют конечной. Еще один способ классификации игр — по свойствам платежной функции. В игре с нулевой суммой общая сумма выигрышей всех игроков равна нулю. То есть в игре с нулевой сумме двух участников выигрыш одного из них равен проигрышу другого. Таким образом, в игре с нулевой суммой существует конфликт между игроками, и поэтому их называют также антагонистическими играми. В общем случае в игре с нулевой суммой, как правило, имеют место и конфликты, и согласованные действия игроков. Прямой противоположностью играм с нулевой суммой являются игры двух игроков с постоянной разностью, в которых оба игрока выигрывают или проигрывают одновременно. Поэтому игрокам выгодно действовать согласованно. В зависимости от характера предварительной договоренности между игроками различают кооперативные и некооперативные игры. Игра является кооперативной, если до ее начала игроки образуют коалиции и принимают взаимообязывающие соглашения о координации своих стратегий. В противоположном случае игра будет некооперативной.
Описание игры в развернутой форме Существует два способа описания и анализа любой конкретной игры: 1) описание игры в развернутой форме 2) описание игры в нормальной форме. Описание игры в развернутой форме предполагает следующее: 1) перечисление ходов, которые могут делать игроки; 2) определение информации, которой располагают игроки в процессе игры; 3) определение возможных вариантов действия игроков; 4) указание предельных размеров платежей в конце игры Этот наиболее детализированный способ описания игр используется для сравнительно простых игр. Их называют позиционными играми, и представляют в виде дерева игры. Способ описания игры в виде дерева игры включает 3 главных момента: 1) чередования ходов, начиная с первого, причем ходы могут быть как личными, так и случайными; 2) возможна недостаточность информации о действиях других участников игры; 3) определение набора исходов игры (вершин дерева) с заданным значением платежной функции. Наиболее часто игры с конечным или бесконечным числом стратегий описываются в нормальной форме. Этот способ описания игры предполагает рассмотрение всех возможных стратегий каждого игрока и определение платежей, соответствующих любым возможным комбинациям стратегий всех игроков. Для иллюстрации рассмотрим бескоалиционную игру.
Бескоалиционные игры Рассмотрим бескоалиционную игру, когда каждый игрок действует самостоятельно. Пусть Процесс игры состоит в выборе каждым игроком своей стратегии Тогда после всех введенных обозначений бескоалиционной игрой называют систему следующего вида:
В бескоалиционной игре все множества являются множествами вещественных чисел. Среди явлений, описываемых посредством бескоалиционных игр, довольно много таких, когда по результатам игры приходится распределять некоторые ресурсы. В теории игр также выделяют игры с постоянной суммой: бескоалиционная игра называется игрой с постоянной суммой, если существует такая константа c, что выполнятся условие
Антагонистические игры. Общие сведения Опр.: Игра Другими словами, антагонистическая игра — это игра двух лиц с нулевой суммой. Обозначив множество стратегий первого игрока через X
Как отмечалось выше, целью исследования является нахождение ситуации равновесия (равновесия в прямом конфликте). Поэтому поведение игроков диктуется: 1-ый игрок старается за счет выбора стратегии 2-ой игрок за счет выбора стратегии Суть этого конфликта состоит в том, что каждый из игроков обладает возможностью менять только свою стратегию. Преодоление этой трудности, другими словами определение наиболее рационального способа поведения игроков в этой игре, это и есть игровая модель принятия решений. Если в антагонистической игре двух лиц множества X и Y конечны, то игра называется матричной. Название объясняется тем, что игру можно представить таким образом: элементы множеств X и Y занумеровываются, например:
Ситуацией в этом случае является пара Рассмотрим матричную антагонистическую игру с матрицей выигрышей:
Первый (максимизирующий) игрок выбирает строку. Второй (минимизирующий) игрок выбирает столбец, на их пересечении записан выигрыш первого игрока. Каждый игрок стремится к увеличению своего выигрыша. Но его выигрыш зависит не только от его выбора, но и от того, какая стратегия будет выбрана противником. Поэтому, стремясь получить максимальный выигрыш, каждый игрок должен учитывать поведение противника. В теории игр выбор оптимальной стратегии предлагается осуществлять, основываясь на принципе минимакса (максимина), который иногда называют «принципом осторожной игры против умного партнера». Вот рассуждения первого игрока, основанные на указанном принципе. «Пусть я выбрал i-ую строку. Тогда самое меньшее, на что я могу рассчитывать, будет Эта величина называется нижним значением игры и обозначается:
Номер строки i, который выбрал первый игрок, называется максиминной стратегией первого игрока. Рассуждения второго игрока, основанные на принципе минимакса. «Пусть я выбрал j-ый столбец. Тогда самое большее, что я могу проиграть — это Величина
Значение j называется минимаксной стратегией 2-ого игрока. Теорема: Если
Доказательство: Так как по определению
Таким образом, Пример. Имеется следующая платежная матрица A(x)
B(y) Нижняя цена игры равна -3, верхняя цена игры равна 4, максиминная стратегия первого игрока есть Если нижняя цена игры равна верхней цене игры, то игра называется игрой с cедловой точкой. Пусть Любая седловая точка является искомой точкой равновесия в игре, так как любое отклонение игроков от оптимальной стратегии приведет к уменьшению выигрыша первого, либо к увеличению проигрыша второго.
S-игра
Играм, в которых у первого игрока конечное число стратегий, можно дать полезную геометрическую интерпретацию. Пусть задана игра Можно рассмотреть множество векторов:
Игра, заданная множеством точек Правила S-игры следующие: второй игрок выбирает одну из точек
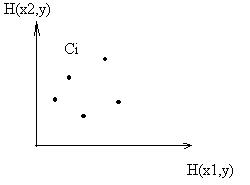
Нетрудно видеть, что S-игра эквивалентна обычной игре в нормальной форме Если число стратегий первого игрока равно двум, то S-игра имеет наглядное геометрическое интерпретацию, т.к. точки множества
Пример: Рассмотрим игру
Обозначим через Теорема. Любая смешанная стратегия второго игрока может быть представлена точкой, принадлежащей выпуклой оболочке Доказательство. Рассмотрим смешанные стратеги игроков
Обозначим через S точку в m-мерном пространстве с координатами
………………………….
Учитывая, что
Видим, что S есть не что иное, как средневзвешенное точек Справедливо и обратное. Так как любая точка S, принадлежащая выпуклой оболочке
Следствие. Поскольку смешанная стратегия первого игрока остается в S-игре той же самой, что и в обычной игре, из доказанной теоремы следует, что S – игра полностью эквивалентна обычной игре, т.е. любая игра может быть представлена в виде эквивалентной S-игры.
Теорема о минимаксе Возможность нахождения каждым игроком своей наилучшей стратегии основывается на следующей теореме, которая может рассматриваться как доказательство существования решения для конечных игр. Теорема. Всякая конечная антагонистическая игра имеет цену, и у каждого игрока существует по меньшей мере одна оптимальная стратегия. Исходные предпосылки. Пусть Нижняя и верхняя цены S-игры будут равны Для того, чтобы доказать теорему, достаточно показать, что Для доказательства этого неравенства достаточно найти такую смешанную стратегию
Действительно, если (1) имеет место, то
Решение матричных игр
Существует несколько основных методов решения матричных игр: 1. Аналитический 2. Графический 3. Итеративный (метод Брауна-Джонсона) 4. Метод линейного программирования Рассмотрим подробнее последний из перечисленных.
ПРИМЕР. Пусть имеется некоторая игра с матрицей A=
A+5 Предположим, что все стратегии рабочие. Составляем систему уравнений: 7t1 + 2t2 + 9t3 - z1 = 1 2t1 + 9t2 - z2 = 1 9t1+11t3 - z3 = 1
Решение этих уравнений при условии t1 + t2 + t3 t1 = 0,05 t2 = 0,1 t3 = 0,05 v(A1) = p2=0,1*5=0,5 p3=0,05*5=0,25 v(A)=v(A1) - 5=0
q1* + q2* + q3* = 1 2q1 + 9q2 = 5 9q1 + 11q3 =5 q2=0,5
Графическое решение игр 2*n и m*2 Рассмотрим игру (2*n) с матрицей
Выигрыш 1-го игрока H(p,yk)=p1a1k + p2a2k = p1a1k + (1-p1)a2k, На плоскости такая зависимость изображается отрезком прямой, причем при p=0 H(p,yk)=a2k, p=1 H(p,yk)=a1k Таким образом, получаем семейство из n прямых:
Исходя из условия гарантированного выигрыша, его величина при разных значениях р будет определяться нижней границей множества этих прямых. Очевидно, что оптимальная стратегия соответствует той точке полученного множества, в которой значение функции максимально, а само это максимальное значение есть значение игры. Рабочими стратегиями 2-ого игрока являются в данном случае 3я и 4я, а значит, оптимальная стратегия 1-ого игрока определяется из системы уравнений: q3 + q4 = 1 a23q3 + a24q4 = v
Рассмотрим теперь игру (m*2) с матрицей Эту игру удобно рассматривать для второго игрока. Как и в предыдущем случае, строится семейство из m отрезков прямых, отображающих зависимость величины функции выигрыша 2го игрока от выбираемой им стратегии: Н(xi,q)= ai1q + ai2(1-q),
Исходя из разумности поведения 1-ого игрока, проигрыш 2-ого определяется верхней огибающей семейства этих прямых. Значения q* и v находятся как абсцисса и ордината нижней вершины огибающей, а затем оптимальная стратегия 2-ого игрока определяется исходя из его рабочих стратегий (в данном случае рабочими стратегиями 2-ого игрока являются xr и xe), аналогично предыдущему случаю. Во всех этих случаях число рабочих стратегий обоих игроков одинаково. Неантагонистические игры N={1,2,…,N} — число игроков (больше двух). Возможны следующие ситуации: 1) совместные действия игроков (коалиции) запрещены по условиям игры, и тогда игра называется бескоалиционной; 2) совместные действия не запрещены, игроки могут образовывать коалиции и действовать совместно. Такие игры называются кооперативными.
Бескоалиционные игры В таких играх каждый игрок действует самостоятельно. Игра Г=<N, {xi}, i Каждый игрок выбирает некоторую стратегию из множества Хi: i Это описание бескоалиционной игры в нормальной форме. Игроки выбирают свои стратегии xi независимо друг от друга. Если для каждого игрока множество стратегий xi конечно, то получаем конечную бескоалиционную игру. Если хотя бы один из игроков имеет бесконечное число стратегий, то это бесконечная бескоалиционная игра. Простейшей бескоалиционной игрой является игра двух лиц. Они могут не только выигрывать или проигрывать, но и делать это совместно (одновременно выигрывать или проигрывать). Опишем такую игру (бескоалиционную) в нормальной форме: Г=<x1,x2,H1,H2>, где {x1,x2}-множество стратегий, H1,H2— функции выигрыша. (x(1),x(2)) Ясно, что если игра конечна, то матрицу Н можно рассмотреть как H1=(aij) m*n A H2=(bij) m*n B Такую игру называют биматричной: Г=<A,B>; aij= -bij,
Библиографический список
1. Петросян Л.А., Зенкевич Н.А., Семина Е.Н. Теория игр.-М.: В.Ш. 1998. 2. Коршунов Ю.М. Математические основы кибернетики. –М.: Энергоатом- издат, 1987. 3. Интрилигатор М. Математические методы оптимизации и математическая теория.- М.: Прогресс, 1975. 4. Карлин С. Математические методы в теории игр, программировании и экономике.- М. Мир.1964. 5. Дюбин Г.Н., Суздаль В.Г. Введение в прикладную теорию игр.- М.: Наука, 1984. 6. Нейман Д., Моргенштерн О. Теория игр и экономическое поведение. М.: Наука, 1970. 7. Гегечкори Е.Т. Математические модели принятия решений в экономике и технике.- Омск, Изд-во ОмГТУ, 2004. 8. Адамчук А.С. и др. Математические модели и игры в экономике: Уч. Пособие, Ставрополь: Сервисшкола, 2004.
Основные понятия теории игр Теория игр представляет собой интенсивно развивающуюся математическую дисциплину, являющуюся одним из разделов теории принятия решений (исследования операций). Предметом исследования теории игр являются методы принятия решений в конфликтных ситуациях. Ситуация называется конфликтной, если в ней сталкиваются интересы нескольких лиц, преследующих противоположные цели. Каждая из сторон может проводить ряд мероприятий для достижения своих целей, причем успех одной стороны означает неудачу другой. Авторы первого фундаментального трактата по теории игр Дж. фон Нейман и О. Моргенштерн ориентировались на анализ конфликтных ситуаций в вопросах экономики, когда при наличии свободной конкуренции в роли борющихся сторон выступают торговые фирмы, промышленные предприятия и т.д. Однако конфликтные ситуации встречаются и во многих других областях. К конфликтным ситуациям относятся почти все ситуации, возникающие при планировании военных операций, выборе системы оружия, охране объектов от нападения, преследовании и перехвате цели и т.п. Интересными примерами конфликтных ситуаций являются спортивные состязания, арбитражные споры, аукционы, выборы в парламент при наличии нескольких кандидатов на одно место. То есть областью применения методов теории игр являются: 1) математика; 2) экономика; 3) военная стратегия и тактика; 4) политика. Приведенные примеры показывают большое разнообразие встречающихся на практике конфликтных ситуаций. Обычно эти ситуации трудны для непосредственного анализа из-за множества второстепенных факторов. Для того, чтобы сделать возможным математический анализ конфликтной ситуации, ее необходимо упростить, учтя только основные факторы. Упрощенную формализованную модель конфликтной ситуации называют игрой, а конфликтующие стороны — игроками или лицами, принимающими решения (если это часть теории принятия решения). Следует различать понятие игры и понятие индивидуальной партии этой игры. Игра представляет собой совокупность правил, описывающих поведение игроков и известных всем игрокам. Каждый случай разыгрывания игры некоторым конкретным образом от начала и до конца представляет собой партию игры. Элементами игры являются ходы. Правила игры предусматривают, какова должна быть последовательность ходов, и указывают характер каждого хода. Также правила регламентируют, какие ходы может осуществлять каждый игрок, какие ситуации могут возникнуть, каков будет выигрыш каждого игрока в каждой из ситуаций. Ход — момент игры, связанный с выбором игроком определенной стратегии поведения (определенного образа действий). Ходы бывают личные и случайные. Личный ход представляет собой выбор игроком одного из заданного множества вариантов. Например, каждый ход в шахматах является личным, причем первый ход — выбор из 20 вариантов. Решение, принятое игроком при личном ходе, называют выбором. Случайный ход также представляет собой выбор одного из множества вариантов, но здесь вариант выбирается не игроком, а некоторым механизмом случайного выбора. Примерами случайных ходов может быть сдача карт или бросание монеты. Выбор, осуществляемый при случайном ходе, называют исходом этого хода. Таким образом, партия — законченная совокупность ходов, после которой можно говорить о выигрыше или проигрыше игроков в данной партии. В общем случае, игру можно рассматривать как бесконечную последовательность партий. Стратегия — набор правил, сформулированных до начала игры.
Классификация игр Классификацию игр проводят по различным признакам: 1) по числу игроков; 2) по числу стратегий; 3) по свойствам платежной функции; 4) по характеру предварительной договоренности между игроками. Игру, в которой участвует n игроков, называют игрой с n участниками. Количество участников может быть равным 2, 3 и т.д. При наличии двух игроков могут возникать конфликтные ситуации, и необходимость в координированных действиях (кооперация). Если в игре участвуют три игрока и более, то могут создаваться коалиции, т.е. группы из двух игроков и более, имеющих общую цель и координирующих свои стратегии. По количеству стратегий различают игры конечные и бесконечные. Если хотя бы из игроков располагает бесконечным множеством стратегий, то игру называют бесконечной. Если же каждый из игроков располагает конечным множеством стратегий, то игру называют конечной. Еще один способ классификации игр — по свойствам платежной функции. В игре с нулевой суммой общая сумма выигрышей всех игроков равна нулю. То есть в игре с нулевой сумме двух участников выигрыш одного из них равен проигрышу другого. Таким образом, в игре с нулевой суммой существует конфликт между игроками, и поэтому их называют также антагонистическими играми. В общем случае в игре с нулевой суммой, как правило, имеют место и конфликты, и согласованные действия игроков. Прямой противоположностью играм с нулевой суммой являются игры двух игроков с постоянной разностью, в которых оба игрока выигрывают или проигрывают одновременно. Поэтому игрокам выгодно действовать согласованно. В зависимости от характера предварительной договоренности между игроками различают кооперативные и некооперативные игры. Игра является кооперативной, если до ее начала игроки образуют коалиции и принимают взаимообязывающие соглашения о координации своих стратегий. В противоположном случае игра будет некооперативной.
Описание игры в развернутой форме Существует два способа описания и анализа любой конкретной игры: 1) описание игры в развернутой форме 2) описание игры в нормальной форме. Описание игры в развернутой форме предполагает следующее: 1) перечисление ходов, которые могут делать игроки; 2) определение информации, которой располагают игроки в процессе игры; 3) определение возможных вариантов действия игроков; 4) указание предельных размеров платежей в конце игры Этот наиболее детализированный способ описания игр используется для сравнительно простых игр. Их называют позиционными играми, и представляют в виде дерева игры. Способ описания игры в виде дерева игры включает 3 главных момента: 1) чередован
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1807; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.32.252 (0.019 с.) |

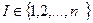 — множество игроков. Каждый из игроков имеет некоторое множество
— множество игроков. Каждый из игроков имеет некоторое множество  своих стратегий. Число стратегий образует множество стратегий каждого игрока, и это число должно быть не меньше двух.
своих стратегий. Число стратегий образует множество стратегий каждого игрока, и это число должно быть не меньше двух. . В результате этого выбора определяется исход партии:
. В результате этого выбора определяется исход партии:  . Пусть
. Пусть  — вектор ситуаций в игре, тогда
— вектор ситуаций в игре, тогда  — множество всех ситуаций в игре. С другой стороны, множество всевозможных ситуаций S можно рассматривать как
— множество всех ситуаций в игре. С другой стороны, множество всевозможных ситуаций S можно рассматривать как  . Выигрыш каждого игрока в каждой ситуации определяется следующим выражением:
. Выигрыш каждого игрока в каждой ситуации определяется следующим выражением: 
 .
. Если
Если  , то бескоалиционная игра называется игрой с нулевой суммой.
, то бескоалиционная игра называется игрой с нулевой суммой. называется антагонистической, если выполняются условия
называется антагонистической, если выполняются условия  и
и  .
. , а множество стратегий второго игрока через Y
, а множество стратегий второго игрока через Y 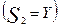 , антагонистическую игру можно описать следующим образом:
, антагонистическую игру можно описать следующим образом: , где
, где 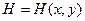 — выигрыш первого игрока или проигрыш второго.
— выигрыш первого игрока или проигрыш второго. максимизировать свой выигрыш (
максимизировать свой выигрыш (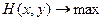 );
); старается минимизировать проигрыш (
старается минимизировать проигрыш ( ).
). и
и  .
. ,
,  ,
, 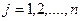 . Выигрыш первого игрока
. Выигрыш первого игрока 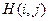 рассматривается как элемент
рассматривается как элемент  матрицы А размером
матрицы А размером 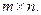 Эта матрица называется матрицей игры. Игра протекает следующим образом: игроки одновременно и независимо друг от друга называют номер строки (первый игрок) и номер столбца (второй игрок). Элемент матрицы, расположенный на пересечении выбранных строки и столбца, и есть выигрыш первого игрока и соответственно проигрыш второго.
Эта матрица называется матрицей игры. Игра протекает следующим образом: игроки одновременно и независимо друг от друга называют номер строки (первый игрок) и номер столбца (второй игрок). Элемент матрицы, расположенный на пересечении выбранных строки и столбца, и есть выигрыш первого игрока и соответственно проигрыш второго.
 . Поэтому естественно выбрать такую строку, чтобы этот минимальный выигрыш был наибольшим:
. Поэтому естественно выбрать такую строку, чтобы этот минимальный выигрыш был наибольшим:  . Таким образом, я могу гарантировать, что меньше, чем
. Таким образом, я могу гарантировать, что меньше, чем  , мой выигрыш быть не может».
, мой выигрыш быть не может». .
. . Поэтому естественно выбрать такой столбец, чтобы этот максимальный проигрыш был наименьшим, т.е. чтобы
. Поэтому естественно выбрать такой столбец, чтобы этот максимальный проигрыш был наименьшим, т.е. чтобы  . Таким образом, я мог бы гарантировать, что меньше, чем
. Таким образом, я мог бы гарантировать, что меньше, чем  , мой выигрыш быть не может».
, мой выигрыш быть не может».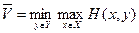 .
.

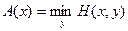 , то, очевидно,
, то, очевидно,  . Так как
. Так как  , то
, то  . Эти неравенства очевидны для любых x, y и для тех, которые обеспечивают верхнюю и нижнюю цены игры:
. Эти неравенства очевидны для любых x, y и для тех, которые обеспечивают верхнюю и нижнюю цены игры: .
.


 , минимаксная стратегия второго игрока есть
, минимаксная стратегия второго игрока есть  .
. , тогда величину с называют ценой игры, а стратегии игроков, обеспечивающие результат с, — оптимальными стратегиями. Клетку матрицы, определяющую величину с, называют седловой точкой, так как значение с является одновременно минимальным элементом строки и максимальным элементом столбца, на пересечении которых стоит эта величина.
, тогда величину с называют ценой игры, а стратегии игроков, обеспечивающие результат с, — оптимальными стратегиями. Клетку матрицы, определяющую величину с, называют седловой точкой, так как значение с является одновременно минимальным элементом строки и максимальным элементом столбца, на пересечении которых стоит эта величина. — цена игры. Если
— цена игры. Если  , то игра является несправедливой, т.к один игрок точно проигрывает. Если
, то игра является несправедливой, т.к один игрок точно проигрывает. Если  .
.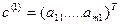 …..
…..  .
. , получила название S-игры.
, получила название S-игры. , а первый игрок выбирает i-ую координату этой точки
, а первый игрок выбирает i-ую координату этой точки  . При этом выигрыш первого игрока, соответственно проигрыш второго, будет равен значению i-ой координаты точки
. При этом выигрыш первого игрока, соответственно проигрыш второго, будет равен значению i-ой координаты точки  , т.е.
, т.е.  .
. , в которой столбцы определяют точки
, в которой столбцы определяют точки  с координатами
с координатами  ).
).
 . Эквивалентная S - игра содержит 5 точек:
. Эквивалентная S - игра содержит 5 точек:  ,
,  ,
,  ,
,  ,
,  . Геометрическое изображение этой игры приведено на рисунке.
. Геометрическое изображение этой игры приведено на рисунке.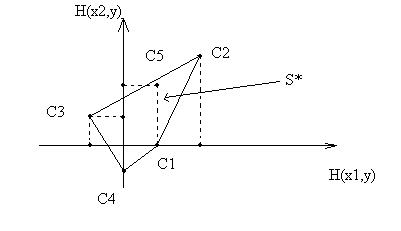
 выпуклую оболочку конечного множества точек
выпуклую оболочку конечного множества точек  может рассматриваться как некоторая смешанная стратегия второго игрока.
может рассматриваться как некоторая смешанная стратегия второго игрока. и
и  . При использовании этих смешанных стратегий проигрыш второго игрока
. При использовании этих смешанных стратегий проигрыш второго игрока , где
, где  .
. :
: ;
; .
.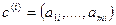 , это выражение можно записать в виде векторного соотношения
, это выражение можно записать в виде векторного соотношения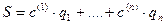 .
. с весами
с весами 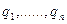 , а следовательно, S есть некоторая точка, принадлежащая выпуклой оболочке
, а следовательно, S есть некоторая точка, принадлежащая выпуклой оболочке 
 — смешанное расширение этой игры. При доказательстве теоремы удобно вести рассуждения в терминах S-игры, поэтому через
— смешанное расширение этой игры. При доказательстве теоремы удобно вести рассуждения в терминах S-игры, поэтому через 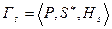 обозначим эквивалентную S-игру.
обозначим эквивалентную S-игру. и
и  соответственно, независимо от того, рассматривают игру G или эквивалентную ей S-игру
соответственно, независимо от того, рассматривают игру G или эквивалентную ей S-игру  , причем
, причем  .
. , так как из сравнения с предыдущим неравенством будет следовать
, так как из сравнения с предыдущим неравенством будет следовать  , т.е. что игра имеет цену.
, т.е. что игра имеет цену.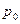 первого игрока, при которой для всех
первого игрока, при которой для всех  . (1)
. (1) . Таким образом, доказательство теоремы будет сводиться к доказательству неравенства (1). Доказательство теоремы опущено (см. напр. Коршунов Ю.М. Математические основы кибернетики).
. Таким образом, доказательство теоремы будет сводиться к доказательству неравенства (1). Доказательство теоремы опущено (см. напр. Коршунов Ю.М. Математические основы кибернетики).
 A1=
A1= 
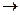 min:
min: = 5
= 5 



 ,
, 

 N, {Hi}, i
N, {Hi}, i  ,
,  , следовательно, игра антагонистическая.
, следовательно, игра антагонистическая.


