
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Чистые и смешанные стратегииСодержание книги Поиск на нашем сайте
Среди конечных игр, имеющих практическое значение, сравнительно редко встречаются игры с седловой точкой; более типичным является случай» когда нижняя и верхняя цена - игры различны. Анализируя матрицы таких игр, мы пришли к заключению, что если каждому игроку предоставлен выбор одной - единственной стратегии., то в расчете на разумно действующего противника этот выбор должен определяться принципом минимакса. Придерживаясь своей максиминной стратегии, мы при любом поведении противника заведомо гарантируем себе выигрыш, равный нижней цене -игры а. Возникает естественный вопрос: нельзя ли гарантировать себе средний выигрыш, больший а, если применять не одну-единственную «чистую» стратегию, а чередовать случайным образом несколько стратегий? Такие комбинированные стратегии, состоящие в применении нескольких чистых стратегий, чередующихся по случайному закону с определенным соотношением частот, в теории игр называются смешанными стратегиями. Очевидно, каждая чистая стратегия является частным случаем смешанной, в которой все стратегии, кроме одной, применяются с нулевыми частотами, а данная — с частотой 1. Оказывается, что, применяя не только чистые, но и смешанные стратегии, можно для каждой конечной игры получить решение, т. е. пару таких (в общем случае смешанных) стратегий, что при применении их обоими игроками выигрыш будет равен цене игры, а при любом одностороннем отклонении от оптимальной стратегии выигрыш может измениться только в сторону, невыгодную для отклоняющегося. Высказанное утверждение составляет содержание так называемой основной теоремы теории игр. Эта теорема была впервые доказана фон Нейманом в 1928 г. Известные доказательства теоремы сравнительно сложны; поэтому приведем только ее формулировку. Каждая конечная игра имеет, по крайней мере, одно решение (возможно, в области смешанных стратегий). Выигрыш, получаемый в результате решения, называется ценой игры. Из основной теоремы следует, что каждая конечная игра имеет цену. Очевидно, что цена игры v всегда лежит между нижней ценой игры а и верхней ценой игры
Действительно, а есть максимальный гарантированный выигрыш, который мы можем себе обеспечить, применяя только свои чистые стратегии. Так как смешанные стратегии включают в себя в качестве частного случая и все чистые, то, допуская, кроме чистых, еще и смешанные стратегии, мы, во всяком случае, не ухудшаем своих возможностей; следовательно,
Аналогично, рассматривая возможности противника, покажем, что
откуда следует доказываемое неравенство (3.1). Введем специальное обозначение для смешанных стратегий. Если, например, наша смешанная стратегия состоит в применении стратегий АЛ,
Аналогично смешанную стратегию противника будем обозначать:
где Предположим, что нами найдено решение игры, состоящее из двух оптимальных смешанных стратегий S, S. В общем случае не все чистые стратегии, доступные данному игроку, входят в его оптимальную смешанную стратегию, а только некоторые. Будем называть стратегии, входящие в оптимальную смешанную стратегию игрока, его «полезными» стратегиями. Оказывается, что решение игры обладает еще одним замечательным свойством: если один из игроков придерживается своей оптимальной смешанной стратегии 5 (5). то выигрыш остается неизменным и равным цене игры v, независимо от того, что делает другой игрок, если он. только не выходит за пределы своих «полезных» стратегий. Он, например, может пользоваться любой из своих «полезных» стратегий в чистом виде, а также может смешивать их в любых пропорциях. Докажем это утверждение. Пусть имеется решение «полезных» стратегий
причем Докажем это следующим образом. Пусть Из определения оптимальной стратегии следует, что любое отклонение противника от стратегии не может быть ему выгодно, поэтому
Посмотрим, может ли хотя бы в одном из трех случаев величина
Очевидно, что если хотя бы одна из величин
21. Решение простейших игр.
Сведение игры к ЗЛП.
Лекция 13. Сведение игры к ЗЛП.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.136 (0.006 с.) |

 :
:

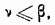
 с частотами
с частотами 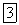 причем
причем  будем обозначать эту стратегию
будем обозначать эту стратегию

 — частоты, в которых смешиваются стратегии
— частоты, в которых смешиваются стратегии 
 игры
игры  . Для конкретнрсти будем считать, что оптимальная смешанная стратегия состоит из смеси трех
. Для конкретнрсти будем считать, что оптимальная смешанная стратегия состоит из смеси трех соответственно состоит из смеси трех «полезных» стратегий
соответственно состоит из смеси трех «полезных» стратегий 

 Утверждается что если мы будем придерживаться стратегии S, то противник может применять стратегии
Утверждается что если мы будем придерживаться стратегии S, то противник может применять стратегии  в любых пропорциях, а выигрыш останется неизменным и по-прежнему будет равен цене игры
в любых пропорциях, а выигрыш останется неизменным и по-прежнему будет равен цене игры 
 будут выигрыши при нашей стратегии 5 и стратегиях противника соответственно
будут выигрыши при нашей стратегии 5 и стратегиях противника соответственно 

 или
или  оказаться больше
оказаться больше  Оказывается, что нет. Действительно, выразим выигрыш v при оптимальных стратегиях
Оказывается, что нет. Действительно, выразим выигрыш v при оптимальных стратегиях  через выигрыши
через выигрыши  Так как в стратегии
Так как в стратегии  применяются с частотами
применяются с частотами  то
то
 была больше
была больше  то и их среднее взвешенное значение (3.2) было бы больше V, что противоречит условию. Таким образом, доказано важное свойство оптимальных стратегий, которое мы будем широко применять при решении игр.
то и их среднее взвешенное значение (3.2) было бы больше V, что противоречит условию. Таким образом, доказано важное свойство оптимальных стратегий, которое мы будем широко применять при решении игр.


