Метод потенциалов решения транспортных задач

Соотношения

определяют систему из m+n-1 линейных уравнений с m+n известными, имеющую бесчисленное множество решений; для её определённости одному неизвестному присваивают произвольное значение (обычно альфа равное 0), тогда все остальные неизвестные определяются однозначно.

Критерий оптимальности

Если известны потенциалы решения Х0 транспортной задачи и для всех незаполненных ячеек выполняются условия α_i+β_j≤ C_ij, то Х0 является оптимальным планом транспортной задачи.

Если план не оптимален, то необходимо перейти к следующему плану (таблице) так, чтобы транспортные расходы не увеличивались.

Цикл перерасчёта таблицы – это последовательность ячеек, удовлетворяющая условиям:

1. Одна ячейка пустая, все остальные занятые.

2. Любые две соседние ячейки находятся в одной строке или в одном столбце.

3. Никакие три соседние ячейки не могут быть в одной строке или в одном столбце.

Пустой ячейке присваивают знак "+", остальным – поочерёдно знаки "–" и "+".

Для перераспределения плана перевозок с помощью цикла перерасчёта сначала находят незаполненную ячейку (r, s), в которой αr+βs > Crs, и строят соответствующий цикл; затем в минусовых клетках находят число X = min(X_ij). Далее составляют новую таблицу по следующему правилу:

4. В плюсовых клетках добавляем Х.

5. Из минусовых клеток вычитаем Х.

6. Все остальные клетки вне цикла остаются без изменения.

Получим новую таблицу, дающую новое решение Х, такое, что F (X₁) ≤ F (X₀); оно снова проверяется на оптимальность через конечное число шагов, обязательно найдем оптимальный план транспортной задачи, ибо он всегда существует.

Найдём оптимальный план для рассмотренной выше задачи. В качестве опорного плана возьмем план, полученный с помощью метода "минимального элемента" Х₁₁= 3, Х₁₂= 12, Х₂₁= 2, Х₂₄= 8, Х₂₅= 15, Х₃₁= 15, Х₃₃= 5. Все остальные элементы равны 0.

Составим систему уравнений для нахождения потенциалов решения, найдем сумму соответствующих потенциалов для каждой свободной ячейки и пересчитаем тарифы (стоимости) для каждой свободной ячейки.

Так как у нас получились отрицательные значения, то полученный план не является оптимальным. Выберем ячейку для пересчета A2B2. Получим:

X = min(2, 12) = 2

Строим следующую транспортную таблицу.

Проверим полученный план на оптимальность. Теперь ячейка A1B2 не заполнена.

Построенный план не является оптимальным, следовательно, производим пересчет. Выберем ячейку A3B5.

X = min(15, 10, 15) = 10

Строим следующую транспортную таблицу.

Проверим построенный план на оптимальность.

Полученный план является оптимальным. Х₁₁= 15, Х₂₂= 12, Х₂₄= 8, Х₂₅= 5, Х₃₁= 5, Х₃₃= 5, Х₃₅= 10. Все остальные Х_ij= 0.

F = 1*15+1*12+3*8+3*5+4*5+1*5+3*10 = 121

 

1. Задачи нелинейного программирования с линейной целевой функцией и нелинейными ограничениями.

Чтобы проиллюстрировать более наглядно различие между линейными и нелинейными задачами, ограничимся решением задачи с двумя переменными, так как решение таких задач может быть представлено графически.

 

17. Задачи нелинейного программирования с линейной целевой функцией и нелинейными ограничениями

 

ограничения q_i(x) либо целевая функция Z(X) либо то и другое нелинейны.
Найти max(min)=Z=z(X)
вобласти
где R – отношение порядка (=, ≥, ≤), Ω– область допустимых решений; _bi– константа, ;
X=(x₁,…,x_n)={x_j}, j=1..n – план или вектор управления.
Для выяснения трудностей решения задач данного класса, порождаемых нелинейностью, сопоставим задачи линейного и нелинейного программирования. Можно указать три характерные особенности для каждого класса.

Задачи линейного программирования	Задачи нелинейного программирования
1. Область Ω допустимых планов – выпуклое множество с конечным числом угловых (крайних) точек.	1. Множество Ω допустимых планов может быть невыпуклым, несвязным, иметь бесконечное число крайних точек.
2. Экстремальное значение линейная целевая функция z(X) достигает в одной из крайних точек (на границе области Ω допустимых решений).	2. Экстремум может достигаться не только на границе, но и внутри области Ω допустимых решений.
3. Экстремальное значение z(X) целевой функции является и глобальным значением.	3. Целевая функция z(X) в области Ω может иметь несколько локальных экстремумов.

На рисунке приводится классификация задач и методов нелинейного программирования.

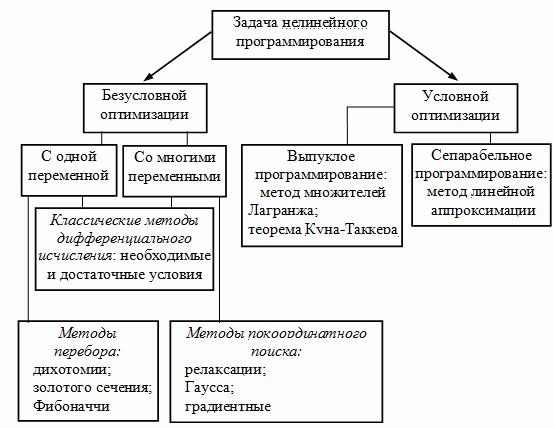
Рисунок - Классификация задач и методов нелинейного программирования

Большинство существующих методов в нелинейном программировании можно разделить на два больших класса:

1. Прямые методы - методы непосредственного решения исходной задачи. Прямые методы порождают последовательность точек – решений, удовлетворяющих ограничениям, обеспечивающим монотонное убывание целевой функции.
   Недостаток: трудно получить свойство глобальной сходимости.
   Задачи с ограничениями в виде равенств.
   Метод замены переменных (МЗП)
2. Двойственные методы - методы, использующие понятие двойственности. В этом случае легко получить глобальную сходимость.
   Недостаток: не дают решения исходной задачи в ходе решения – оно реализуемо лишь в конце итерационного процесса.
• Метод множителей Лагранжа (ММЛ)

Нелинейное программирование

Прямые методы

Метод множителей Лагранжа. В задачах 301-320 используя метод множителей Лагранжа найти точки экстремума функции z=f(x,y) при заданном условии: z=xy+7x, 2x+y=1