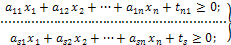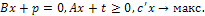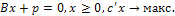Общая формулировка задачи линейного программирования

Естественной формой задачи линейного программирования является задача об определении максимума линейной целевой функции, обычно называемой линейной формой,

(1)

при соблюдении m линейных равенств и s линейных неравенств

(2)

1.

(3)

Значения x_i(i=1, 2,..., n), удовлетворяющие всем условиям (2) и (3), называются допустимыми решениями. Значения х_i(i=1, 2,..., n), являющиеся допустимыми и сообщающие форме (1) максимальное значение, называются оптимальным планом задачи.

Уравнения (2) при m_i. Это будет только в том случае, если ранг матрицы В, составленной из коэффициентов уравнений (2), максимальный и равен m

 

Неравенства (3) определяют в n-мерном пространстве неизвестных х_i выпуклый многогранник. Неравенство

(4)

называется жестким, если выполнение какой-то группы неравенств из остальных неравенств (3) превращает (4) в строгое равенство. В противном случае неравенство (4) называется нежестким. Например, неравенство -х+а≥0 будет жестким, если х-a≥0, и неравенство –х+а≥0 будет нежестким, если х-b≥0 при b<а.

Неравенство (4) несовместно с остальными неравенствами (3), если среди всех х⁰, удовлетворяющих s-1 неравенству (3), нет х, удовлетворяющего (4). В противном случае неравенство (4) совместно с остальными неравенствами (3).

Многогранник, описанный условиями - неравенствами (3), является выпуклым телом (n-мерным выпуклым телом), если ранг матрицы А, составленной из коэффициентов при неизвестных в неравенствах, равен мин (s, n) и среди неравенств (3) нет жестких. Другими словами, если существуют некоторые значения x⁰_i(i=1, 2,..., n), при которых все неравенства (3) являются строгими,

то многогранник - выпуклое тело. В двухмерном пространстве (на плоскости) многогранник (3) - плоский многоугольник. В трехмерном пространстве это многогранник в обычном понимании. В пространствах большей размерности многогранник (3) - обобщенное понятие, перенесенное из трехмерного представления.

Система неравенств –х₁-х₂-...-x_n+1≥0, xi≥0 (i=1, 2,..., n) выделяет n-мерную пирамиду с основанием в виде гиперповерхности, наклоненной под одинаковыми углами ко всем координатным осям, вершиной в начале координат (х=0) и длиной каждого ребра, равной единице. Такой многогранник называется симплексом.

Сечение многогранника, определенного условиями (3), линейным многообразием, заданным уравнениями (2), есть множество допустимых решений задачи, которое в свою очередь есть выпуклый (n-m) - мерный многогранник. Координаты вершин этого многогранника называются множеством опорных планов задачи. Оптимальный план находится в этом множестве.

ВЕКТОРНО-МАТРИЧНАЯ ФОРМУЛИРОВКА ЗАДАЧИ. Вводятся следующие векторы и матрицы: x=(x₁, х₂,..., х_n)′- вектор неизвестных, с=(с₁, с₂, …, с_n)′ - вектор цен (термин из экономической трактовки задачи) или вектор коэффициентов целевой функции, t=(t₁, t₂, …, t_δ)′ - вектор в неравенствах и p=(p₁, p₂,..., р_m)′ - вектор в равенствах. Так же вводятся матрицы: В размером m×n, составленная из коэффициентов при неизвестных в уравнениях (2) и А размером s×n, составленная из коэффициентов при неизвестных в неравенствах (3). Символ (′) означает транспонирование вектора или матрицы. В таких обозначениях задача о максимуме (1) при ограничениях (2) и (3) записывается в весьма компактной форме

(5)

НОРМАЛЬНАЯ ФОРМА ЗАДАЧИ. В такой форме среди s неравенств (3) имеются условия неотрицательности всех переменных, которые выделяются в отдельную группу условий

В нормальной форме отсутствуют уравнения (2), а задача формулируется только с помощью ограничений - неравенств

(6)

Здесь матрица А не включает условия х≥0.

Условие х≥0 задает так называемые несвободные переменные в отличие от задачи (5), где все переменные свободные, т. е. ограничений по знаку нет.

КАНОНИЧЕСКАЯ ФОРМА ЗАДАЧИ. В этой форме ограничения записаны только в виде равенств для несвободных переменных

(7)

Переход от нормальной формы к канонической возможен введением дополнительных s переменных x_n+i(i=1, 2,..., s) - по числу неравенств в нормальной форме, и расширением матрицы А на s столбцов присоединением единичной матрицы размером s×s

(8)

Считая новые переменные (n+s)-мерным вектором х=(х₁, х₂,..., x_n+s)′, приходим к канонической форме задачи (7), в которой следует считать p=t.

СМЕШАННАЯ ФОРМА ЗАДАЧИ. Эта форма содержит в качестве ограничений равенства и неравенства и отличается от естественной формы тем, что все переменные несвободные

Определение минимума целевой функции. В тех случаях, когда вместо максимума линейной формы (1) требуется определить минимум, тогда вводится обратная по знаку целевая функция F(x)=-f(x)=-с′х, для которой определяется максимальное значение. В этом случае - мин (-с′х)=макс (с′х) при одних и тех же ограничениях задачи.

 

 

Геометрический метод реше