
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности транспортной задачи.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Характерными особенностями транспортных моделей являются: 1) наличие не менее двух исходных пунктов поставки; 2) наличие не менее двух конечных пунктов потребления; 3) из каждого исходного пункта в каждый конечный пункт поставляется однородная продукция – хлысты, сортименты, пиломатериалы и пр.; 4) известны или можно определить величины, характеризующие объем продукции, поставляемой из каждого исходного пункта, – мощность по отгрузке каждого исходного пункта; 5) известны или можно определить объемы продукции, потребляемые в каждом пункте назначения, – мощность по приемке каждого из пунктов потребления; 6) известны или можно определить себестоимость (затраты) или прибыль перевозки единицы продукции из каждого исходного пункта в каждый пункт потребления. Цель, достигаемая решением транспортной задачи, – определение такого количества продукции, которое следует транспортировать из каждого исходного пункта в каждый пункт назначения и при котором транспортные расходы будут минимальными или прибыль (в линеаризованных задачах) от транспортировок будет максимальна. Какова цель – минимизация затрат на транспортировку или максимизация прибыли – таков и выбор критерия. На рис. 5.18 изображена транспортная модель в виде сети с т исходными пунктами и п пунктами назначения. Исходным пунктам и пунктам назначения соответствуют вершины (окружности), а маршрутам транспортировки – дуги (прямые линии). Количество продукции, отгружаемое (производимое) в каждом пункте i, обозначим через аi, а потребляемое (хранимое) в каждом пункте j – через bj; сij – себестоимость транспортировки единицы продукции из каждого исходного пункта i в каждый пункт назначения j.
Обозначим через xij – количество продукции (объемы), перевозимое из исходного пункта i в пункт назначения j. Тогда задача ЛП транспортного типа в общем виде формулируется следующим образом: минимизировать у= при ограничениях весь объем транспортировки из каждого i -го пункта не может быть больше, чем там имеется в наличии:
весь объем транспортировки в каждый j -й пункт должен быть, по крайней мере, равен спросу (потребности) этого пункта: xij Если суммарный объем исходных пунктов (поставщиков) равен суммарному объему пунктов потребления (потребителей), Σ аi =Σ bj, то модель называется сбалансированной транспортной моделью. В реальных производственных ситуациях не всегда соблюдается изложенное условие – объем поставок равен объему потребления. Поэтому с целью упрощения процесса решения транспортную модель искусственно приводят к сбалансированной посредством введения фиктивных исходных пунктов или фиктивных пунктов назначения. В этом случае в выражения ограничений (5.14) – при введении фиктивного исходного пункта – или (5.15) – при введении фиктивного пункта потребления – вносятся соответствующие дополнения. Стоимость транспортировки из фиктивного исходного в фиктивный пункты потребления принимается равной нулю.
15.Опорный план транспортной задачи Метод северо-западного угла Пусть условия транспортной задачи заданы таблице 2.3. Пример 2.6.1 Метод минимальной стоимости Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел ai, или bj . Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены. Метод аппроксимации Фогеля Данный метод состоит в следующем: 1. на каждой итерации находят разности между двумя наименьшими тарифами во всех строках и столбцах, записывая их в дополнительные столбец и строку таблицы; 2. находят max Δcij и заполняют клетку с минимальной стоимостью в строке (столбце), которой соответствует данная разность. Процесс продолжается до тех пор, пока все грузы не будут развезены по потребителям. Данный метод в ряде задач приводит к оптимальному плану. Решим этим методом задачу из примера 2.6.1 (см. табл.2.7).
Метод двойного предпочтения Если таблица стоимостей велика, то перебор всех элементов затруднителен. В этом случае используют метод двойного предпочтения, суть которого заключается в следующем.
Метод потенциалов.
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.250.241 (0.009 с.) |


 (5-13)
(5-13)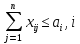 =
=  (5.14)
(5.14) , j =
, j =  ; (5.15)
; (5.15) i =
i = 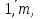 j=. (5.16)
j=. (5.16)


