
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод множителей Лагранжа для функций n переменныхСодержание книги Поиск на нашем сайте
Допустим, мы имеем функцию n переменных z=f(x1,x2,…,xn) и m уравнений связи (n>m): φ1(x1,x2,…,xn)=0;φ2(x1,x2,…,xn)=0,…,φm(x1,x2,…,xn)=0. Обозначив множители Лагранжа как λ1,λ2,…,λm, составим функцию Лагранжа: F(x1,x2,…,xn,λ1,λ2,…,λm)=f+λ1φ1+λ2φ2+…+λmφm Необходимые условия наличия условного экстремума задаются системой уравнений, из которой находятся координаты стационарных точек и значения множителей Лагранжа: ⎧⎩⎨⎪⎪∂F∂xi=0;(i=1,n¯¯¯¯¯¯¯)φj=0;(j=1,m¯¯¯¯¯¯¯¯) Выяснить, условный минимум или условный максимум имеет функция в найденной точке, можно, как и ранее, посредством знака d2F. Если в найденной точке d2F>0, то функция имеет условный минимум, если же d2F<0, – то условный максимум. Можно пойти иным путем, рассмотрев следующую матрицу:
Определитель матрицы ∣∣∣∣∣∣∣∣∣∣∣∣∂2F∂x21∂2F∂x2∂x1∂2F∂x3∂x1…∂2F∂xn∂x1∂2F∂x1∂x2∂2F∂x22∂2F∂x3∂x2…∂2F∂xn∂x2∂2F∂x1∂x3∂2F∂x2∂x3∂2F∂x23…∂2F∂xn∂x3……………∂2F∂x1∂xn∂2F∂x2∂xn∂2F∂x3∂xn…∂2F∂x2n∣∣∣∣∣∣∣∣∣∣∣∣, выделенной в матрице L красным цветом, есть гессиан функции Лагранжа. Используем следующее правило: · Если знаки угловых миноров H2m+1,H2m+2,…,Hm+n матрицы L совпадают с знаком (−1)m, то исследуемая стационарная точка является точкой условного минимума функции z=f(x1,x2,x3,…,xn). · Если знаки угловых миноров H2m+1,H2m+2,…,Hm+n чередуются, причём знак минора H2m+1 совпадает с знаком числа (−1)m+1, то исследуемая стационарная точка является точкой условного максимума функции z=f(x1,x2,x3,…,xn).
2. Чистые и смешанные стратегии. 3. Решение простейших игр.(учебник) 4. Сведение игры к ЗЛП. Игра Пусть игра задана платежной матрицей
Оптимальная стратегия Для оптимальной стратегии все средние выигрыши не меньше цены игры v, поэтому получаем систему неравенств:
Каждое из неравенств можно разделить на число
Цель игрока А – максимизировать свой гарантированный выигрыш, т.е. цену игры v. Разделив на Это задача линейного программирования. Решая задачу (1*)–(2*), получаем оптимальное решение Для определения оптимальной стратегии
которые следуют из того, что средний проигрыш игрока В не превосходит цены игры, какую бы чистую стратегию не применял игрок А. Если обозначить
Переменные Игра свелась к следующей задаче. Определить значения переменных
Решение задачи линейного программирования (5*), (6*) определяет оптимальную стратегию. При этом цена игры Составив расширенные матрицы для задач (1*), (2*) и (5*), (6*), убеждаемся, что одна матрица получилась из другой транспонированием: Таким образом, задачи линейного программирования (1*), (2*) и (5*), (6*), являются взаимно-двойственными. Очевидно, при определении оптимальных стратегий в конкретных задачах следует выбрать ту из взаимно-двойственных задач, решение которой менее трудоемко, а решение другой задачи найти с помощью теорем двойственности. При решении произвольной конечной игры размера рекомендуется придерживаться следующей схемы: 1.Исключить из платежной матрицы заведомо невыгодные стратегии по сравнению с другими стратегиями. Такими стратегиями для игрока А (игрока В) являются те, которым соответствуют строки (столбцы) с элементами, заведомо меньшими (большими) по сравнению с элементами других строк (столбцов). 2.Определить верхнюю и нижнюю цены игры и проверить, имеет ли игра седловую точку. Если седловая точка есть, то соответствующие ей стратегии игроков будут оптимальными, а цена совпадает с верхней (нижней) ценой. 3.Если седловая точка отсутствует, то решение следует искать в смешанных стратегиях. Для игр размера т х п рекомендуется симплексный метод, для игр размера 2х2,2хn,mх2 возможно геометрическое решение.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.147.193 (0.009 с.) |


 в общем случае не имеет наглядной геометрической интерпретации. Ее решение достаточно трудоемко при больших т и п, однако принципиальных трудностей не имеет, поскольку может быть сведено к решению задачи линейного программирования. Покажем это.
в общем случае не имеет наглядной геометрической интерпретации. Ее решение достаточно трудоемко при больших т и п, однако принципиальных трудностей не имеет, поскольку может быть сведено к решению задачи линейного программирования. Покажем это.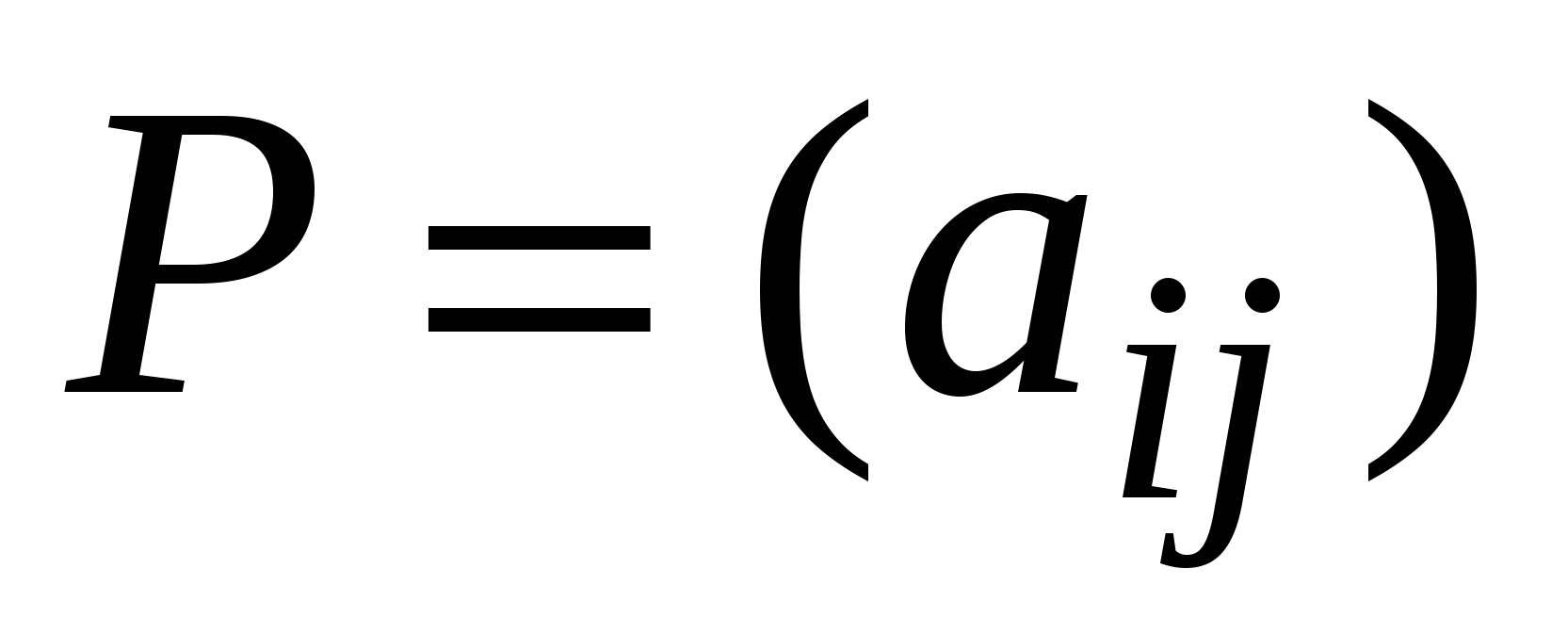
 . Игрок А обладает стратегиями
. Игрок А обладает стратегиями 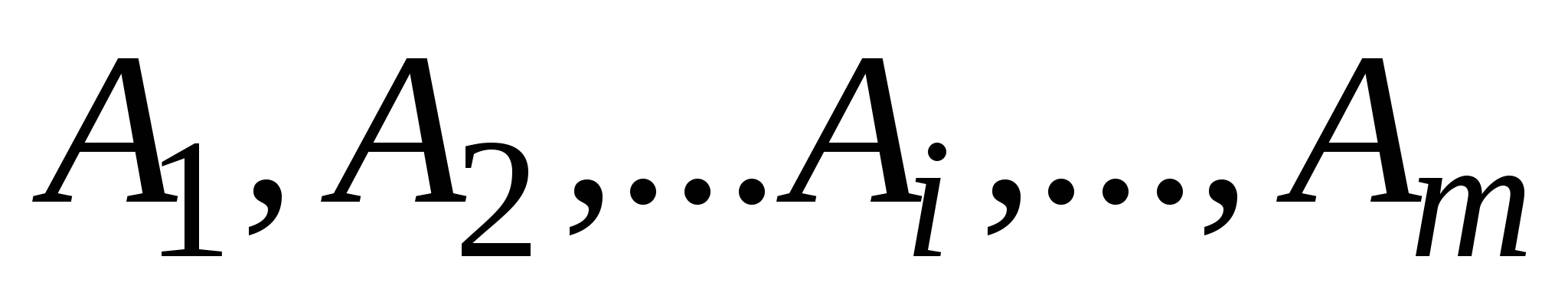 , игрок В – стратегиями
, игрок В – стратегиями  . Необходимо определить оптимальные стратегии
. Необходимо определить оптимальные стратегии 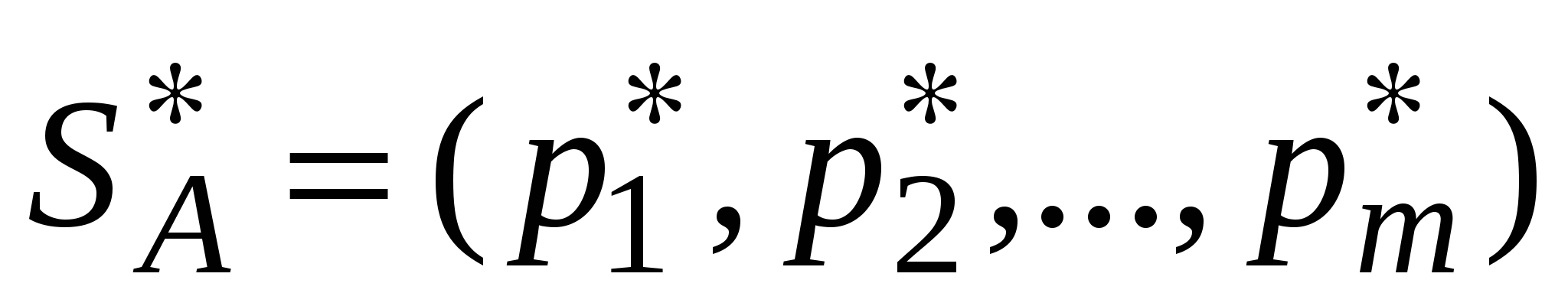 и
и  , где
, где  – вероятности применения соответствующих чистых стратегий
– вероятности применения соответствующих чистых стратегий  ,
, ,
,  .
. удовлетворяет следующему требованию. Она обеспечивает игроку А средний выигрыш, не меньший, чем цена игры v, при любой стратегии игрока В и выигрыш, равный цене игры v, при оптимальной стратегии игрока В. Без ограничения общности полагаем v > 0; этого можно добиться, сделав все элементы
удовлетворяет следующему требованию. Она обеспечивает игроку А средний выигрыш, не меньший, чем цена игры v, при любой стратегии игрока В и выигрыш, равный цене игры v, при оптимальной стратегии игрока В. Без ограничения общности полагаем v > 0; этого можно добиться, сделав все элементы  . Если игрок А применяет смешанную стратегию против любой чистой стратегии
. Если игрок А применяет смешанную стратегию против любой чистой стратегии  игрока В, то он получает средний выигрыш, или математическое ожидание выигрыша
игрока В, то он получает средний выигрыш, или математическое ожидание выигрыша  (т.е. элементы j-гo столбца платежной матрицы почленно умножаются на соответствующие вероятности стратегий и результаты складываются).
(т.е. элементы j-гo столбца платежной матрицы почленно умножаются на соответствующие вероятности стратегий и результаты складываются).
 . Введем новые переменные:
. Введем новые переменные:  . Тогда система принимает вид
. Тогда система принимает вид (1*)
(1*) равенство, получаем, что переменные
равенство, получаем, что переменные  удовлетворяют условию:
удовлетворяют условию:  . Максимизация цены игры v эквивалентна минимизации величины
. Максимизация цены игры v эквивалентна минимизации величины 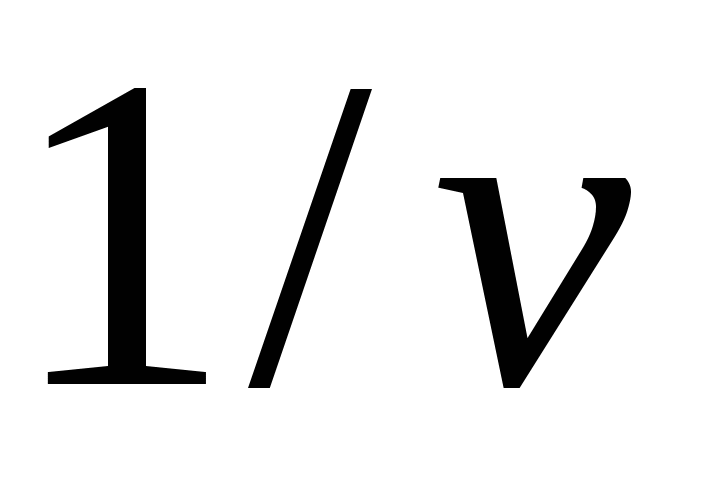 , поэтому задача может быть сформулирована следующим образом: определить значения переменных
, поэтому задача может быть сформулирована следующим образом: определить значения переменных  , maк, чтобы они удовлетворяли линейным ограничениям (*) и при этом линейная функция
, maк, чтобы они удовлетворяли линейным ограничениям (*) и при этом линейная функция  (2*) обращалась в минимум.
(2*) обращалась в минимум. и оптимальную стратегию.
и оптимальную стратегию. следует учесть, что игрок В стремится минимизировать гарантированный выигрыш, т.е. найтиmax. Переменные
следует учесть, что игрок В стремится минимизировать гарантированный выигрыш, т.е. найтиmax. Переменные  удовлетворяют неравенствам
удовлетворяют неравенствам (3*)
(3*) (4*), то получим систему неравенств:
(4*), то получим систему неравенств: (5*)
(5*) удовлетворяют условию
удовлетворяют условию  .
.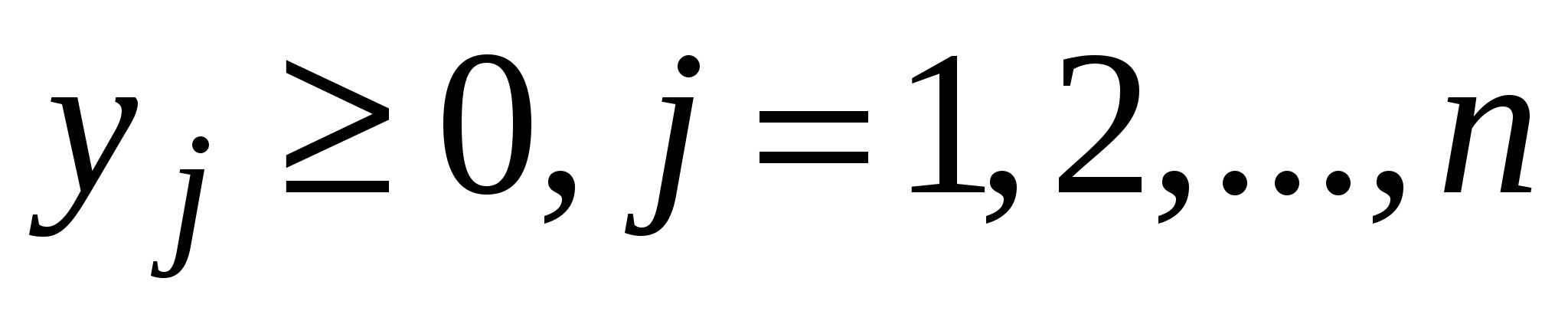 , которые удовлетворяют системе неравенств (5*) и максимизируют линейную функцию
, которые удовлетворяют системе неравенств (5*) и максимизируют линейную функцию (6*)
(6*) . (7*)
. (7*)


