
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ матричных игр двух игроков с нулевой суммой в смешанных стратегиях.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В предыдущем разделе предполагалось, что игроки делают ровно по одному ходу независимо друг от друга. Предположим, что число ходов неограничено, на каждом ходу может быть выбрана любая стратегия, но с некоторой вероятностью. Величину выигрыша относим к одному ходу, но в данной постановке она является случайной величиной. Таким образом, для каждого игрока выбору подлежит закон распределения выбора той или иной стратегии. Определение. Смешанной стратегией игрока называется полный набор вероятностей применения его чистых стратегий. Таким образом, если игрок 1 имеет m чистых стратегий 1,2, ..., m, то его смешанная стратегия x – это набор чисел x =(x 1, ..., xm) T, удовлетворяющих соотношениям xi ³0, i =1,2,3,…, m, Чистая стратегия есть частный случай смешанной стратегии. Действительно, если в смешанной стратегии какая–либо i –я чистая стратегия применяется с вероятностью 1, то все остальные чистые стратегии не применяются. И эта i– я чистая стратегия является частным случаем смешанной стратегии. Для соблюдения секретности каждый игрок применяет свои стратегии независимо от выбора другого игрока. Средний выигрыш игрока 1 в матричной игре с матрицей А выражается в виде математического ожидания его выигрышей и равен Е (А, х, y)=á x, Ay ñ= Первый игрок стремится за счёт изменения своих смешанных стратегий х максимально увеличить свой средний выигрыш Е (А, х, y), а второй – за счёт своих смешанных стратегий стремится сделать Е (А, х, y) минимальным. Верхняя и нижняя границы игры будут иметь соответственно вид Подобно играм, имеющим седловые точки в чистых стратегиях, вводится понятие равновесия в игре Определениие. Под состоянием равновесия в игре будем понимать пару смешанных стратегий (x 0, y 0), для которых Е (А, х, y 0)£ Е (А, х 0, y 0)£ Е (А, х 0, y), т.е. отклонение любого (только одного) из игроков от этой стратегии приводит к ухудшению (неулучшению) его критерия. Величина Е (А, х 0, y 0) называется ценой игры и обозначается через q. Как и для игр с чистыми стратегиями, возникает вопрос о существовании состояния равновесия в играх со смешанными стратегиями. На него отвечает следующая основная теорема матричных игр: Теорема (о минимаксе). Для матричной игры с любой матрицей А величины Таким образом, можно записать:
Не все матричные игры имеют ситуацию равновесия в чистых стратегиях. Однако всякая матричная игра имеет ситуацию равновесия в смешанных стратегиях. Задача линейного программирования эквивалентна в определенном смысле матричной игре. Рассмотрим антагонистическую игру с матрицей A, размерностью (m ´ n). Выпишем симметричные двойственные задачи линейного программирования с этой матрицей следующего вида
где u – вектор, все компоненты которого равны 1, размерность соответствует размерности вектора x, аналогично вектор w, размерность которого соответствует размерности ветора y. Справедлива следующая теорема. Теорема. Пусть матрица положительна (все элементы положительны), тогда: 1. Задачи (3.2.1), (3.2.2) имееют решения, при этом
2. значение игры v равно
для того, чтобы стратегии
где
Пусть матрица A ¢ произвольная матрица размерностью (m ´ n), тогда существует константа b >0 такая, что матрица A = A ¢+ B, B ={ bij }, bij = b, i =1,2,3,…, m, j =1,2,3,…, n, сторого положительная и для нее существует состояние равновесия x *, y *. Можно показать, что состояние равновесия x *, y * также является состоянием равновесия и в игре с матрицей A ¢, значение игры в ней равно 1/ q – b. Алгоритм поиска состояния равновесия 1. По матрице A ¢ строится строго положительная матрица A = A ¢+ B, B ={ bij }, bij = b, i =1,2,3,…, m, j =1,2,3,…, n, 2. Строятся двойственные задачи (3.2.1), (3.2.2) и находятся их оптимальные решения 3. Находится равновесное состояние Рассмотрим эту связь на примере антагонистической игры с матрицей A ¢, имеющей вид: A ¢= Поставим матрице A в соответствие следующие двойственные задачи:
В этих задачах w =(1,1) T u =(1,1) T. Решением этих задач является: x 1 =1/17, x 2 =4/17; y1 =3/17, y2 =2/17; значение функционала q =5/17. x 1* =1/5, x 2* =4/5, y1* =3/5, y2* =2/5, значение игры v =1/ q – b =17/5–1=12/5.
Самостоятельная работа №6 Найти решение матричной игры в смешанных стратегиях для следующих матриц:
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 442; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.43.228 (0.007 с.) |

 = 1. Аналогично для игрока 2, который имеет n чистых стратегий, смешанная стратегия y – это набор чисел y =(y 1, ..., yn), yj ³ 0, (j = 1,2,3,…, n),
= 1. Аналогично для игрока 2, который имеет n чистых стратегий, смешанная стратегия y – это набор чисел y =(y 1, ..., yn), yj ³ 0, (j = 1,2,3,…, n),  = 1.
= 1. = xTAy.
= xTAy. Е (А, х, y),
Е (А, х, y),  Е (А, х, y).
Е (А, х, y). Е (А, х, y) и
Е (А, х, y) и 

 ,
, были равновесными, необходимо и достаточно, чтобы
были равновесными, необходимо и достаточно, чтобы ,
, – оптимальные решения соответственно задач (3.2.1), (3.2.2)
– оптимальные решения соответственно задач (3.2.1), (3.2.2) . Положим b =1, матрица A примет вид A ¢=
. Положим b =1, матрица A примет вид A ¢=  .
. ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,

 ,
,
 ,
,


 ,
,
 ,
,
 ,
,
 ,
,
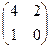 ,
,
 ,.
,.
 ,
,
 ,
,
 ,
,
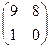 ,
,
 ,
,
 ,
,
 ,
,



