
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ матричных антагонистических игр двух игроков .Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим биматричную игру с нулевой суммой. Пусть для первого игрока X 1={1,2,..., m }, для второго X 2={1,2,..., n }. Выбираемые стратегии будем обозначать соответственно i и j. Каждой паре стратегий (i, j) поставлено в соответствие некоторое число j 1(i, j)= аij, выражающее выигрыш игрока 1, j 2(i, j)=– аij – выигрыш 2–го игрока (аij – его проигрыш). Для первого игрока предпочтителен выбор пары (i, j), увеличивающий значение аij. Для второго игрока предпочтителен выбор пары (i, j), уменьшающий значение аij. Эту модель будем записывать так
Такая игра является антагонистической игрой двух лиц. Допустим, что каждый из игроков делает один ход: игрок 1 выбирает свою i –ю стратегию i =1,2,3,…, m, а игрок 2 – свою j –ю стратегию j =1,2,3,…, n. После выполнения ходов игрок 1 получает выигрыш аij за счёт игрока 2 (если аij< 0, то это значит, что игрок 1 платит второму сумму | аij |). На этом игра заканчивается. Стратегии игроков i =1,2,3,…, m, и j =1,2,3,…, n будем называть чистыми стратегиями. Если рассмотреть матрицу А = то проведение каждой партии матричной игры с матрицей А сводится к выбору игроком 1 i –й строки, а игроком 2 j –го столбца и получения игроком 1 (за счёт игрока 2) выигрыша аij. Введем понятие гарантированных стратегий игроков. В это понятие вложим следующий смысл: стратегия игрока называется гарантированной, если применение этой стратегии обеспечивает выигрыш, который не может быть уменьшен при всевозможных стратегиях другого игрока. Исходя из этих позиций, игрок 1 исследует матрицу выигрышей А следующим образом: для каждого значения i =1,2,3,…, m определяется j (i), для которого значение выигрыша по стратегиям 2–го игрока минимально
Среди значений i =1,2,3,…, m и соответствующих им значений j (i) выбирается то значение i 1, j 1= j (i 1) для которого
Это выражение можно переписать
Определение 3. 1. Число Игрок 2 при при поиске своего гарантированного проигрыша должен стремится по возможности за счёт своих стратегий максимально уменьшить выигрыш игрока 1. Поэтому для игрока 2 определяется с начала для каждого j =1,2,3,…, n определяется i (j), для которого
т.е. для каждого j =1,2,3,…, n определяется величина наибольшего проигрыша. Затем среди этих проигрышей выбирается наименьший, т.е. выбираем j 2 и соответственно i 2= i (j 2), для которых
при условии, что игрок 2 применит свою j –ю чистую стратегию, затем игрок 2 отыскивает такую свою j = j 2 стратегию, при которой он получает гарантированный проигрыш, т.е. находит
Определение 3. 2. Число Другими словами, применяя свои чистые стратегии, игрок 1 может обеспечить себе выигрыш не меньше Определении 3. 3. Под состоянием равновесия в игре будем понимать пару чистых стратегий (i 0, j 0), для которых Не трудно видеть, что точка (i 0, j 0) является седловая точкой функции аij, i = 1,2,..., m, j = 1,2,..., n. Вопрос о существовании равновесия в матричной игре двух игроков с нулевой суммой определяется следующей теоремой. Теорема. Для того, чтобы в задаче существовала седловая точка, необходимо и достаточно, чтобы
Таким образом, исходя из (3.3), седловой элемент
Пример 1. Пусть Всю информацию по матрице и результаты анализа запишем в таблицу:
Точкой равновесия является пара (i 0; j 0)=(3,1), при которой Пример 2 Пусть Всю информацию по матрице и результаты анализа запишем в таблицу:
Из анализа матрицы выигрышей видно, что
Рассмотрим некоторые широко известные содержательные игры, имеющие конечные множества стратегий. Пример 3. Два игрока кладут одновременно на стол по монете. Если обе монеты выложены одной стороной, то они достаются первому игроку, в противном случае они достаются второму игроку. Для нее матрица игры будет иметь вид
Пример 4. Игра Морро. Игроки одновременно показывают не более m пальцев и в тоже время называют число, не большее n. Если число, названное одним из игроков, совпадает с общим числом пальцев, то игрок получит от своего противника выигрыш равный этому числу. Если оба угадают верно, то чистый платёж будет равен нулю. Таблица игры для случая m =2, n =4 будет иметь вид. В ней skl означает, l – показанных пальцев, k – названное число первым игроком. Аналогично tkl для второго игрока.
Пример 5. Оборона города («Игра полковника Блотто») Полковник Блотто имеет т полков, а его противник — n полков. Противник защищает две позиции. Позиция будет занята полковником Блотто, если на ней наступающие полки окажутся в численном превосходстве. Противоборствующим сторонам требуется распределить полки между двумя позициями. Определим выигрыш полковника Блотто (игрока 1)на каждой позиции. Если у него на позиции полков больше, чем у противника (игрока 2), то его выигрыш на этой позиции равен числу полков противника плюс один (занятие позиции равносильно захвату одного полка). Если у игрока 2полков на позиции больше, чем у игрока 1,то игрок 1теряет все свои полки на этой позиции и еще единицу (за потерю позиции). Если обе стороны имеют одинаковое число полков на позиции, то имеет место ничья и каждая из сторон ничего не получит. Общий выигрыш игрока 1равен сумме выигрышей на обеих позициях. Игра, очевидно, антагонистическая. Опишем стратегии игроков. Пусть, для определенности, т>п. Игрок I имеет следующие стратегии: х 0=(т,0) — послать все полки на первую позицию, xl =(т—i, i)—(m–i) полков послать на первую позицию, а i — на вторую, х m = (0, m). Противник имеет такие стратегии: У 0=(п,0), у 1=(п —i, i),..., у„ =(0, п). Так, при m =4, n = 3, рассмотрев всевозможные ситуации, получим матрицу выигрышей этой игры:
Самостоятельная работа № 5. 1. Составить матрицу игры Морро для случаев, представленных в таблице, и найти состояние равновесия (если оно существует). Номера вариантов записаны в таблице на пересечении строк и столбцов в части таблицы, обведенной двойной линией.
2. Составить матрицу игры полковника Блотто для случаев, представленных в таблице, и найти состояние равновесия (если оно существует).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 617; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.008 с.) |


 ,
,

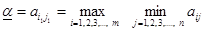
 , определённое по формуле (3. 1), называется нижней чистой це н ой игры и показывает, какой выигрыш может гарантировать себе игрок 1, применяя свои чистые стратегии при всевозможных действиях игрока 2.
, определённое по формуле (3. 1), называется нижней чистой це н ой игры и показывает, какой выигрыш может гарантировать себе игрок 1, применяя свои чистые стратегии при всевозможных действиях игрока 2. ,
,

 , определяемое по формуле (3.2), называется чистой верх н ей ценой игры и показывает, какой проигрыш за счёт своих стратегий может себе гарантировать игрок 2.
, определяемое по формуле (3.2), называется чистой верх н ей ценой игры и показывает, какой проигрыш за счёт своих стратегий может себе гарантировать игрок 2. .
. , т.е. отклонение любого (только одного) из игроков этой стратегии приводит к ухудшению (неулучшению) его критерия.
, т.е. отклонение любого (только одного) из игроков этой стратегии приводит к ухудшению (неулучшению) его критерия.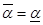
 является минимальным в i 0 –й строке и максимальным в j 0 – м столбце в матрице А. Отыскание седловой точки матрицы А происходит следующим образом: в матрице А последовательно в каждой строке находят минимальный элемент и проверяют, является ли этот элемент максимальным в своём столбце. Если да, то он и есть седловой элемент, а пара стратегий, ему соответствующая, образует седловую точку. Пара чистых стратегий (i 0, j 0) игроков 1 и 2, образующая седловую точку и седловой элемент
является минимальным в i 0 –й строке и максимальным в j 0 – м столбце в матрице А. Отыскание седловой точки матрицы А происходит следующим образом: в матрице А последовательно в каждой строке находят минимальный элемент и проверяют, является ли этот элемент максимальным в своём столбце. Если да, то он и есть седловой элемент, а пара стратегий, ему соответствующая, образует седловую точку. Пара чистых стратегий (i 0, j 0) игроков 1 и 2, образующая седловую точку и седловой элемент  .
.

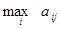

 . Заметим, что хотя выигрыш в ситуации (3;3) также равен
. Заметим, что хотя выигрыш в ситуации (3;3) также равен  .
.



 , т.е. данная матрица не имеет точки равновесия.
, т.е. данная матрица не имеет точки равновесия.



