
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача отыскания кратчайшего расстояния в сети между парами вершинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Постановка задачи. Пусть задан ориентированный граф G =á E, V, H ñ, в котором для каждой дуги v Î V задана длина сv. На множестве вершин E выделены две вершины н и к (соответственно начало и конец пути). Требуется среди всех путей н = i 0, v 1, i 1, v 2, i 2, ..., vk, ik = к, соединяющих вершины t и s, где h 1(vj)= ij– 1, h 2(vj)= ij, j =1,2,3,…, k, с длиной
путь 2 – 1, v 1, 3, v 7, 5, v 12, 6, v 14, 9. Если считать, что длины всех дуг равны 1, то длина первого пути равна 3, длина второго пути равна 4. Не трудно видеть, что длина кратчайшего пути равна 3, и кратчайший путь не единственный.
Алгоритм Беллмана – Калабы Обозначим через Wi длину кратчайшего пути от вершины i до вершины к. Согласно принципа оптимальности Беллмана
Значение Wн будет длиной кратчайшего пути от вершины н до вершины к. Для кратчайшего пути н = i 0, v 1, i 1, v 2, i 2, ..., vk, ik = к справедливо равенство Первый этап. 0– шаг (задание начального приближения). j – ый шаг. (j =1,2,3, ...)
Если после двух следующих друг за другом итерациях j и (j+ 1) Второй этап. 0– шаг. Положить j – ый шаг (j =1,2,3, ...) Положить Если Пример. Пусть граф имеет следующий вид:
Эти длины также записаны на графе рядом с дугами.
Шаг 0. Заполнения столбца «шаг 0» очевидно.
Значения поместим в граф рядом с вершинами
Шаг 1. Заполнение клетки (6, шаг 1) очевидно. Вычислим
Жирным выделены дуги, на которыхдостигается минимум при вычислении W 1. Выполняя аналогичным образом 4 шага получим
Для восстановления оптимального пути используем столбец шага 2, движение начинаем из вершины 1, для нее запомнена дуга v 3. По этой дуге попадаем в вершину 2, из вершины 2 по дуге v 4 в вершину 4, т.д. Таким образом, оптимальный путь следующий (1, v 3,2, v 4,4, v 8,5, v 10,6), его длина равна Алгоритм Флойда. Пусть Wi – верхние оценки кратчайших расстояний от вершины i до вершины к, для самой вершины к Wк =0. Если для всех дуг v Î V выполняется Алгоритм. Первый этап. 0– шаг (задание начального приближения). Положить для всех iÎE\ { к } Wi =¥, для i=к Wк =0; j – ый шаг. (j =1,2,3,...) Среди всех дуг v Î V ищем дугу (обычно в порядке нумерации), для которой Второй этап. Если Wн < ¥, то выполняем второй этап алгоритма Беллмана–Калабы, в противном случае задача решения не имеет. Пример. В качестве примера рассмотрим предыдущую задачу. Для нее таблица, которую уже внесено начальное приближение имеет вид: На графе ищем дугу, для которой
Таковой является v 6, для нее h 1(v 6)=2, h 2(v 6)=6, поэтому полагаем W 2=4+ W 6=4, заменяем значения в клетке 2 на (4, v 6), получим
Следующей будет дуга v 6, поэтому полагаем W 1=1+ W 2=4, поэтому
И так далее, на последнем шаге получим таблицу
Восстанавливая по этой таблице путь путь, получим ранее полученное решение.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 653; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.009 с.) |

 , определить путь, длина которого минимальна.
, определить путь, длина которого минимальна. На графе, изображенном на этом рисунке, выделено 2 пути из вершины 1 в вершину 9: путь 1 – 1, v 2, 4, v 9,7, v 16, 9,
На графе, изображенном на этом рисунке, выделено 2 пути из вершины 1 в вершину 9: путь 1 – 1, v 2, 4, v 9,7, v 16, 9,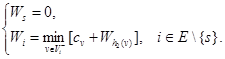
 . Алгоритм Белмана–Калабы представляет собой аналог метода простой итерации. Начальное приближение имеет вид
. Алгоритм Белмана–Калабы представляет собой аналог метода простой итерации. Начальное приближение имеет вид , где M – достаточно большое число, например заведомо большее, чем длина самого длинного пути.
, где M – достаточно большое число, например заведомо большее, чем длина самого длинного пути.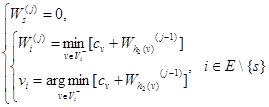
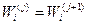 для всех i Î E, то полагаем
для всех i Î E, то полагаем  для всех iÎE. Если Wн ³ M, то задача не имеет решения (нет путей между вершинами н и к), в противном случае переходим к выполнению второго этапа.
для всех iÎE. Если Wн ³ M, то задача не имеет решения (нет путей между вершинами н и к), в противном случае переходим к выполнению второго этапа.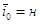 .
. ,
, , то алгоритм прекращает работу, в противном случае переходим к следующему шагу.
, то алгоритм прекращает работу, в противном случае переходим к следующему шагу. Для него длины дуг заданы в таблице:
Для него длины дуг заданы в таблице:
 , в клетку (1, шаг 1) вносим (¥,–). Далее вычислим
, в клетку (1, шаг 1) вносим (¥,–). Далее вычислим 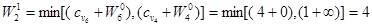 , минимум достигается на дуге v 6. И так далее, получим значения остальных клеток шага 1.
, минимум достигается на дуге v 6. И так далее, получим значения остальных клеток шага 1.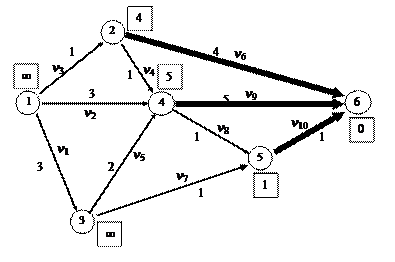
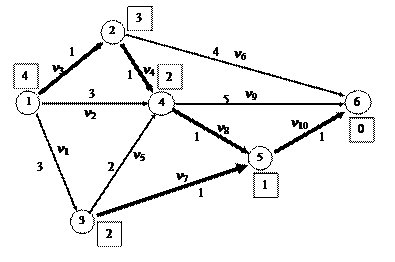
 .
. , то оценки Wi дают кратчайшие расстояния от вершины i до вершины к. Заметим, что если некоторая дуга v Î V содержится в кратчайшем пути из некоторой вершины i (например из вершины h 1(v)) в вершину s, то для нее
, то оценки Wi дают кратчайшие расстояния от вершины i до вершины к. Заметим, что если некоторая дуга v Î V содержится в кратчайшем пути из некоторой вершины i (например из вершины h 1(v)) в вершину s, то для нее  . Если нашлась дуга v Î V, для которой
. Если нашлась дуга v Î V, для которой  ,то оценки Wi не дают кратчайшие расстояния от вершин i до вершины s так как оценку
,то оценки Wi не дают кратчайшие расстояния от вершин i до вершины s так как оценку 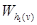 можно улучшить, положив
можно улучшить, положив  , если такой дуги не существует, то переходим к выполнению второго этапа, в противном случае полагаем
, если такой дуги не существует, то переходим к выполнению второго этапа, в противном случае полагаем 



