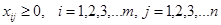Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм расчета потенциаловСодержание книги
Поиск на нашем сайте
В данном алгоритме введен механизм пометок. Строка или столбец помечены знаком '+', если соответствующий потенциал найден, знаком '–' в противном случае. В начале все строки и столбцы таблицы помечаем символом '–' 1 – ый шаг. u 1:=0, 1–ую строку помечаем символом '+' (это означает, что потенциал для данной строки найден). k – ый шаг. a) Для каждой строки i, помеченной символом '+', выполнить: для каждого столбца j =1,2,3,..., n такого, что клетка (i, j) базисная и j – ый столбец помечен символом '–' vj:= ui+cij,столбец помечаем символом '+'. b) Для каждого столбца j, помеченного символом '+', выполнить: для каждой строки i= 1,2,3,..., n такой, что клетка (i, j)базисная, и i –я строка помечена символом '–' ui:= vj–cij,строку помечаем символом '–'. k – шаг выполняем до тех пор, пока все строки и столбцы не станут помеченными символами '+'.
Проверка критерия оптимальности Для того, чтобы базисное решение xij, i= 1,2,3,..., m, j= 1,2,3,..., n,было оптимальным, необходимо и достаточно, чтобы для всех i= 1,2,3,..., m, j= 1,2,3,..., n было справедливо неравенство dij = vj–ui–cij £0. Таким образом, для проверки найденного решения на оптимальность достаточно выполнить следующий алгоритм 1. Для всех i= 1,2,3,..., m, j= 1,2,3,..., n положить dij = vj–ui–cij. 2. Найти такие (k, p), что d kp =max{ dij| i= 1,2,3,..., n, j= 1,2,3,..., m } 3. Если dkp £0, то полученное базисное решение является оптимальным и транспортная задача решена, иначе необходимо перейти к новому базису. Алгоритм перехода к новому базису. Вводим в базис клетку (k, p). Для определения клетки (q, l), выводимой из базиса, воспользуемся следующим алгоритмом: 1. Строим последовательность клеток П ={(i 1, j 1), (i 2, j 2), ... (i, j), ...)}такую, что a) (k, p)Î П; b) все остальные клетки базисные; с) последовательность П образует цикл (смотри транспортную задачу в сетевой постановке). 2. Задаем направление обхода этого цикла, совпадающего с направлением k Þ p. В клетку (k, p)заносим символ '+'. Для остальных клеток (i, j)Î П, если направление i Þ j совпадает с направлением обхода цикла с направлением обхода цикла, то заносим в позицию q символ '+', в противном случае заносим '–'. 3. Определяем клетку (q, l), для которой х (q, l)=min xij, где (i, j) – пробегает все клетки из П, помеченные символом '–'. Полагаем Q = x (q, l).Из базиса выводится клетка (q, l). 4. Для всех (i, j)Î П, если клетка помечена символом '+', то полагаем xij = xij + Q, в противном случае xij = xij – Q. 5. Перейти к выполнению проверки критерия оптимальности. Замечание 1. Иногда минимум достигается на нескольких клетках одновременно. В этом случае в качестве клетки (q, l) выбирается произвольно только одна из них. Замечание 2. При заполнение таблицы для нового базиса значения xij вносятся только в базисные клетки. Пример. Рассмотрим пример, в котором требуется решить транспортную задачу методом потенциалов. Значения ai, bj, cij (i =1,2,3, j =1,2,3,4), заданы в таблице
Начинаем с определения исходного базиса методом северо–западного угла. Таковым является клетка (1,1), для нее x 11=min (11,10)=10, это число заносим в эту клетку. Изменяем a 1 и b 1. Так как b 1=0, затемняем столбец j= 1.
В незатемненной части таблицы северо–западный угол (1,2), для нее x 12=min (1,16)=1, это число заносим в эту клетку. Изменяем a 1 и b 2. Так как a 1=0, затемняем строку i= 1.
Продолжая аналогично далее, получим следующую таблицу:
В ней восстановлены значения ai, bj, а также затемнены базисные клетки. Значение функционала на этом решении будет равно F =2´10+7´1+4´15+3´2+3´12+7´12=213. Алгоритм поиска начального базиса может быть достаточно произвольным. В результате должно получиться решение, удовлетворяющее требованиям: 1. 2. Число базисных клеток должно быть равно n + m –1.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.009 с.) |

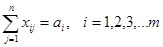 ,
,