Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи дискретного программирования.Содержание книги
Поиск на нашем сайте
Многие задачи исследования операций такие, как задачи распределения ресурсов, сетевого планирования и управления, календарного планирования, размещения, замены оборудования – описываются математическими моделями дискретного программирования. По структуре математической модели задачи дискретного программирования делятся на следующие классы: 1. Задачи с неделимостями. 2. Экстремальные комбинаторные задачи. 3. задачи на несвязных выпуклых областях. 4. задачи с разрывными целевыми функциями. Рассмотрим задачу дискретного программирования в виде
Если множество Х является конечным или счетным, то поставленная задача является задачей дискретного программирования. Если в частном случае компоненты векторов x являются целыми числа, то перед нами задача целочисленного программирования. В задачах дискретного программирования область допустимых решений не является связной, поэтому не является выпуклой в обычном понимании. Отыскание решения таких задач сопряжено со значительными трудностями. Для решения задач дискретного и целочисленного программирования разработаны специальные методы. Эти методы делятся на 3 группы: · методы отсечения; · комбинаторные методы; · методы случайного поиска и эвристические методы.
Методы отсечения для решения задач целочисленного линейного программирования. Рассмотрим задачу целочисленного линейного программирования
Методы отсечения заключаются в следующем. Решается задача без условия целочисленности, если решение получилось целочисленным, то задача решена, в противном случае строится дополнительное органичение, отсекающее это нецелочисленное решение, но оставляющее целочисленное решение исходной задачи. И процедура повторяется. Опишем более подробно применительно к задаче (5.2). Пусть эта задача решена без условия целочисленности. Ее решение достигается на базисном решении, неограничивая общности его, можно записать x =(xB, x ¢) T. На последнем шаге симлекс-метода из симплекс-таблицы можно выразить
где b – столбец свободных членов симплекс-таблицы, A – матрица симплекс-таблицы, соответствующая вектору внебазисных переменных x ¢. Если у вектора все компоненты целочисленны, то задаче решена, в противном случае строим отсечение. Выделим из системы (5.3) строку, соответствующую нецелочисленной компоненте вектора b, получим
Отсечение Данцига. Если решение дробное, то по крайней мере одна из внебазисных переменных не равна 0, учитывая условие целочисленности, она должна быть больше или равна 1. Так как мы эта переменная не известна, то должно выполняться неравенство
Отсечение Гомори. Отсечение Данцига оказалось не эффективным, были построены задачи, в которых бесконечное число таких отсечений не приводило к решению. Несколько позже Гомори разработал несколько видов отсечений на другой основе. Первое отсечение Гомори имеет вид
Им доказано, что при специальном выборе строки, по которой строится отсечение, его алгоритм сходится за конечное число шагов. Отметим, что после приведения этого неравенства к каноническому виду
получаем, что переменную y можно включить в базис, но базис получаем не допустимым, так как –bj <0. Но так как в последней симплекс-таблице все оценки di ³0, то решение задачи можно продолжить двойственным симплекс-методом.
Пример.
xi ³ 0, xi – целые, i =1,2.
Приведем задачу к каноническому виду и занесем данные в симплекс-таблицу:
Решив эту задачу без условия целочисленности, получим симплекс-таблицу.
Из этой таблицы получаем X 1=0. 67, X 2=0. 67, т.е. решение не целочисленное, строим дополнительное ограничение по первой строке (можно и по второй): – 0. 67 Y 1 – 0. 67 Y 2 £ – 0. 67. Приводим его к каноническому виду – 0. 67 Y 1 – 0. 67 Y 2 + Y 3= – 0. 67 и приписываем к симплекс-таблице:
Решаем двойственным симплекс-методом:
Получим целочисленное решение X 1=0, X 2=1, Y 1=1, Y 2=0, Y 3=0,
Самостоятельная работа № 10. Решить задачу 5.2, в которых:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 416; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.141.244 (0.011 с.) |

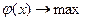 , x Î Х
, x Î Х

 .
.