
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Транспортные задачи линейного программированияСодержание книги
Поиск на нашем сайте
Транспортная задача линейного рограммирования является одной из самых распространенных специальных задач линейного программирования. Первая строгая постановка задачи принадлежит Хичкоку, и поэтому в зарубежной литературе иногда её называют проблемой Хичкока. Первый точный метод решения транспортной задачи был разработан российскими учеными Л.В. Канторовичем и М.К. Гавуриным. В настоящей работе рассмотрены два варианта постановок транспортной задачи: сетевая и матричная. Транспортная задача в сетевой постановке Пусть G =á E, V, H ñ c вязный ориентированный граф, где Е – множество вершин, V – множество ориентированных дуг, H – отображение H: V®E´E, H (v)=(h 1(v), h 2(v)). Вершину h 1(v) будем называть началом дуги v, h 2(v)– ее концом. V+i – множество дуг, входящих в вершину i, V-i – множество дуг, выходящих из вершины i. Все вершины графа делятся на пункты производства (источники) и пункты потребления (стоки)потока. Для каждой вершины iÎЕ известна величина, задающая объем производства или потребления i –ой вершины, причем, если bi< 0, то вершина i – пункт производства (источник), если bi> 0, то i –я вершина – пункт потребления (сток) потока, если bi =0, то вершина i – промежуточная вершина. Для каждой дуги v Î V задана величина cv, характеризующая стоимость перевоза единицы груза по данной дуге. Задача состоит в том, чтобы определить количество перевозимого груза xv по каждой дуге vÎV при условии, что весь поток из пунктов производства будет вывезен, потребности всех пунктов потребления будут удовлетворены и суммарная стоимость транспорта потока будет наименьшей. Приведем формализованную постановку данной задачи:
где (6.1) – минимизируемый функционал (суммарная стоимость перевоза потока), (6.2) – уравнение материального баланса, т.е. суммарный поток, входящий в вершину, минус суммарный поток, выходящий из вершины, должен быть равен объему потока, производимому (потребляемому) в i –ом пункте, соотношение (6.3) означает, что транспортируемый поток движется только в направлении дуг графа G. Если задача (6.1)–(6.3) разрешима, то Метод потенциалов решения данной задачи предполагает, что на исходном графе некоторым способом определено начальное исходное базисное дерево G¢ =á E, V', H ñ, (его дуги будем называть базисными), по которому осуществляется перевозка груза таким образом,
Для определения величин xvÎV' можно воспользоваться следующим алгоритмом: Алгоритм 1. 0 – шаг. E¢:= E. k– й шаг. Если E¢ ¹Æ, то найти вершину, для которой (|V'+i|+|V' –i| =1) {т.е. вершина i концевая на G¢ =á E', V', H ñ}. Если |V'+i| =1, то для дуги v Î V'+i выполнить: xv:= bi, Если |V' –i| =1, то для дуги v Î V' –i выполнить: xv:=– bi, Перейти к следующему шагу. Замечание. В результате работы алгоритма может получиться недопустимое решение: т.е. для некоторых v Î V xv< 0. В этом случае следует сменить исходное базисное дерево. Однако это не гарантирует, что на нем будет получено допустимое решение. Далее будет описан алгоритм, позволяющий либо определить базисное решение, либо доказать, что его не существует. Будем считать, что исходное базисное дерево G’ найдено и для v Î V' определены xv> 0. Для того, чтобы определить, является ли полученное решение оптимальным, воспользуемся следующим критерием оптимальности: Критерий оптимальности: Пусть xv, v Î V, – такое решение задачи (6.1) – (6.3), что для vÎV\V' xv =0 и для v Î V' xv ³0. Это решение оптимально тогда и только тогда, когда существуют числа ui, i Î E,называемые потенциалами, такие, что
Если переменные ui, i Î E, интерпретировать как цены перевозимой продукции, то выписанные зависимости интерпретируются так. По дуге, по которой перевозится продукция цена в конце равна цене в начале плюс стоимость перевозки. В оптимальном решении по дуге не везется продукция, когда цена в конце дуги меньше цены в начале плюс стоимость перевозки. (В оптимальном решении по дуге не везется продукция, если цена в конце дуги меньше суммы: цена в начале плюс стоимость перевозки). Для расчета потенциалов применяется следующий алгоритм:
Алгоритм 2 . 0–шаг. Для произвольной (только одной) вершины iÎE полагаем ui:=0; k– шаг. Найти дугу v Î V', для которой известен потенциал, только одной из ее вершин. Если такой дуги нет, то конец работы, в противном случае используя зависимость Алгоритм 3 . 1. Среди всех дуг vÎV\V' ищем дугу v 0такую, что 2. Если такой дуги нет, то исходная задача (6.1)–(6.3) решена, иначе следует выполнить алгоритм 4 перехода к новому базисному дереву.
Алгоритм 4. V':= V' È{ v 0}, где v 0 дуга, найденная в Алгоритме 3. Теперь граф G' =á E, V', H ñсодержит ровно один цикл G'' =á E'', V'', H ñ, причем v 0 ÎV'. На подграфе G'' задаем направление обхода, совпадающее с направлением дуги v 0, и пропускаем по подграфу G'' в направлении обхода дополнительный поток, величиной q. Каждой дуге v Î V'' приписываем символ «+ q», если направление дуги v совпадает с направлением обхода, и символ «– q» в противном случае. Полагаем q =min xv среди v Î V”, которым приписан символ «– q». Полагаем Для всех v Î V"\ { v 0}: xv:= xv+ q, если дуге v приписан знак + q; xv:= xv– q, если дуге v приписан знак – q. Из множества V’\ { v 0} исключаем дугу, для которой xv =0. Если таких дуг несколько (вырожденный случай), то удаляем только одну так, чтобы не нарушилась связность графа G' =á E, V’, H ñ. Для полученного решения заново вычисляем Алгоритмом 2 потенциалы и анализируем его на оптимальность A лгоритмом 3, и т.д. до тех пор, пока не будет найдено оптимальное решение.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.34.93 (0.007 с.) |

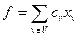
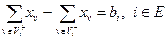 ,
,
 . Легко видеть, что она является задачей линейного программирования и может быть решена алгоритмом симплекс-метода. Однако сетевая структура задачи позволяет разработать более эффективные методы ее решения. Таковым является метод потенциалов для решения транспортных задач.
. Легко видеть, что она является задачей линейного программирования и может быть решена алгоритмом симплекс-метода. Однако сетевая структура задачи позволяет разработать более эффективные методы ее решения. Таковым является метод потенциалов для решения транспортных задач.
 .
.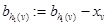 .
.

 , определяем потенциал в вершине, в которой он неизвестен, и переходим к (k +1) шагу.
, определяем потенциал в вершине, в которой он неизвестен, и переходим к (k +1) шагу. ;
; ;
;


