
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача о максимальном потоке в сети.Содержание книги
Поиск на нашем сайте Пусть задан ориентированный граф G =á E, V, H ñ, в котором направление каждой дуги v Î V означает направление движения потока (например, поток автомобилей), пропускная способность каждой дуги равна dv. На множестве вершин E выделены две вершины н и к. Вершина н является источником потока, к – стоком. Требуется определить максимальный поток, который может быть пропущен из вершины н в к. Обозначим через xv величину потока, движущегося по дуге v. Очевидно, что
В каждой вершине iÎE\ { н, к } объем потока входящего равен объему потока выходящего, т.е. справедливо равенство
Соответственно для вершин н и к выполняется
Величина Q является величиной потока, который выходит из вершины н и входит в вершину к. Задача. Определить
при ограничениях (7.13) – (7.16). Величины (Q, xv, vÎV) удовлетворяющие ограничениям (7.13) – (7.16) будем называть потоком в сети, и если они максимизируют величину Q, то максимальным потоком. Нетрудно видеть, что значения Q =0, xv =0, v Î V, являются потоком в сети. Задача (7.13) – (7.16) является задачей линейного программирования и ее можно решить алгоритмами симплекс-метода. Разобьем множество вершины E на две непересекающиеся части E 1 и E 2 таким образом, чтобы н Î E 1, к Î E 2. Разрезом R (E 1, E 2), разделяющим н и к будем называть множество R (E 1, E 2)Ì V такое, что для каждой дуги v Î R (E 1, E 2) либо h 1(v)Î E 1и h 2(v)Î E 2, либо h 1(v)Î E 2и h 2(v)Î E 1. Так на следующем рисунке множество E 1={1,4,7}, эти вершины имеют темную заливку. E 2={2,3,5,6,8,9}. Разрезом R (E 1, E 2) являются дуги, через которые прошла пунктирная линия.
Разобьем множество R (E 1, E 2) на две частиследующим образом: R+ (E 1, E 2)={ v Î R (E 1, E 2) | h 1(v)Î E 1и h 2(v)Î E 2} R– (E 1, E 2)={ v Î R (E 1, E 2) | h 2(v)Î E 1и h 1(v)Î E 2} Элементы множества R+ (E 1, E 2) будем называть прямыми дугами, они ведут из множества E 1, в E 2. Элементы множества R– (E 1, E 2) – обратными дугами, они ведут из множества E 2, в E 1. Потоком через разрез будем называть величину
Пропускной способностью разреза будем называть величину
Очевидно, что 0£ X (E 1, E 2)£ D (E 1, E 2). Справедлива следующая теорема. Теорема 1. (О максимальном потоке и минимальном разрезе). В любой сети величина максимального потока Q из источника н в сток к равна минимальной пропускной способности D (E 1, E 2) среди всех разрезов R (E 1, E 2), разделяющих вершины н и к. Разрез
Пусть (Q, xv, v Î V) – некоторый поток в сети, и последовательность н = i 0, v 1, i 1, v 2, i 2, ..., vK, iK = к, является цепью, соединяющих вершины н и к. Зададим на этой цепи направление движения от вершины н к к. Дуга vj из этой цепи называется прямой, если ее направление совпадает с направлением движения от н к к, и обратной в противном случае. Эту цепь будем называть цепью увеличения потока, если для прямых дуг v цепи (dv– xv)>0 и для обратных xv> 0. По этой цепи можно пропустить дополнительный поток q из н к к величиной q =min(q 1, q 2), где q 1=min(dv – xv), минимум берется по всем прямым дугам цепи, q 2=min(xv), минимум берется по всем обратным дугам цепи. Теорема 2. Поток (Q, xv, vÎV), максимальный тогда и только тогда, когда не существует пути увеличения потока. Предлагаемый алгоритм решения задачи о максимальном потоке в сети основан на поиске цепи увеличения потока из н в к. Этот поиск в свою очередь основан на процессе расстановки пометок вершин, аналогичный алгоритму Дейкстры. Каждой вершине i припишем пометку Pi =[ gi, vi, q ], где gi – величина дополнительного потока, поступившего в вершину i, vi – дуга, по которой поступил поток, q – знак «+», если поток поступил по дуге vi , направленной в i (по прямой дуге; q – знак «–», если поток поступил по дуге vi , направленной от i (по обратной дуге), Будем говорить, что вершина i 1. Не помечена, если до нее не дошел дополнительный поток. Эта пометка будет иметь вид Pi =[0,–, q ], 2. Помечена, но не просмотрена, если до нее поток дошел, но не пропущен дальше, пометка будет иметь вид Pi =[ gi, vi, q ], где gi >0. 3. Помечена и просмотрена, если до нее поток дошел и пропущен дальше, пометка будет иметь вид Алгоритм. П.0. Для всех v Î V полагаем xv =0, полагаем Q= 0. П.1. Все вершины делаем непомеченными. Вершину н делаем помеченной, но не просмотренной с пометкой Pн =[¥,–,–]. Это означает, что в эту вершину поступает поток неограниченного объема. П.2. Ищем помеченную, но не просмотренную вершину. Если такой нет, то найденный поток Q, xv, v Î V, максимальный и алгоритм заканчивает работу. Если такая вершина нашлась, i – ее номер, то переходим к П.3. П.3 (просмотр вершины i). a) для всех положить j = h 2(v), если вершина j не помечена и (dv – xv)>0, то пометить ее с пометкой Pj =[ q, v,+], где q =min(qi, (dv – xv)), если j = к, то перерейти к П4; b) для всех положить j = h 1(v), если вершина j не помечена и xv >0, то пометить ее с пометкой Pj =[ q, v,–], где q =min(qi, xv), если j = к, то перерейти к П4; c) пометить вершину i как просмотренную П.4 (пропуск дополнительного потока). d) Положить j = к, q = gк; e) Положить v = vj, если q =«+», то выполнить: {положить xv = xv + q, i = h 1(v), если i = н, то перейти к П.1, иначе положить j=i и перейти к e) } если q =«–», то выполнить: {положить xv = xv – q, i = h 2(v), если i = н, то перейти к П.1, иначе положить j=i и перейти к e) }
В результате выполнения этого алгоритма будет получен поток (Q, xv, vÎV). Для поиска разреза с минимальной пропускной способностью следует поступить так. На последнем этапе работы алгоритма в П.2 часть вершин будет помечена и просмотрена, эти вершины включим в множество Пример. Для графа, приведенного на следующем рисунке, найти максимальный поток, который будет пропущен из 1–ой вершины в 6–ю. Величины пропускных способностей указаны около дуг.
На нулевом шаге в качестве начального потока может быть взят любой (допустимый). Пусть это будет поток, величины которого в затемненных квадратиках..
Для этого случая Q =4, потоки по дугам приведены в таблице
Шаг 1.
Шаг 2. Просматриваем вершину 1. Выходящие дуги v 1, v 2, v 3, но только для v 2 (dv–xv)>0, поэтом вершина 4 получает пометку [2, v 2,+]. Входящих дуг нет, поэтому дополнительно помеченных вершин нет. Вершина 1 получается помеченной и просмотренной.
Шаг 3. Помеченная не просмотреная вершина 4, из нее вершина 5 получает пометку
Шаг 4. Просматриваем вершину 2. Из нее помечается вершина 6, она получает пометку [1, v 6,+].
Эта вершина концевая, поэтому дополнительный поток, который придет в эту вершину q =1. Переходим к восстановлению цепи, по которой может быть пропущен поток и изменению потоков. Шаг 5 (начало восстановления цепи пропуска дополнительного потока). Полагаем Q = Q + q =4+1=5. В вершину 6 дополнительный поток поступил по дуге v 6, направление дуги прямое (смотри пометку этой вершины), поэтому полагаем Шаг 6. В вершину 2 дополнительный поток поступил по дуге v 4, направление дуги обратное (смотри пометку вершины 2), поэтому полагаем Шаг 7. В вершину 4 дополнительный поток поступил по дуге v 2, направление дуги прямое, поэтому полагаем
Начинаем работу алгоритма вновь, взяв за начальное приближение получившийся поток. Подробно описывать каждый шаг не будем, так как их описание аналогично предыдущему, приведем только таблицы с результатами вычислений. Шаг 1.
Шаг 2. Просматривая вершину 1, получим
Шаг 3. Просматривая вершину 4 получим
Шаг 4. Просматривая вершину 5 получим
Шаг 4. Просматривая вершину 3 получим
Все вершины, которые были помечены, просмотрены, однако вершина 6 не достигнута. Получен максимальный поток. Ответ: Q=5, значения потоков по дугам приведены в таблице:
Покажем, как можно получить разрез, на котором максимальный поток совпадает с его пропускной способностью. Вершины, просмотренные на шаге 4 образуют множество E 1={1,3,4,5}, E 2= E\E 1={2,6}. Выделим на графе вершины из E 1={1,3,4,5} толщиной окружности и заливкой
Дуги между выделенными и невыдененными вершинами образуют искомый разрез. На графе они также выделены, и по ним проведена пунктирная линия. Из рисунка видно, что дуга v 4 разреза обратная, остальные дуги этого разреза прямые. Просчитаем пропускную способность этого разреза Рассчитаем пропускную способность некоторого произвольного разреза и поток по нему, например, по разрезу, изображенному на следующем рисунке
D ({1,2,3},{4,5,6}= X ({1,2,3},{4,5,6}= 0£ X ({1,2,3},{4,5,6}£ D ({1,2,3},{4,5,6}. Можно показать (это следует из условия сохранения потока в вершинах), что величина потока не зависит от разреза. Самостоятельная работа 17. Для графа, имеющего вид
найти: a) максимальный поток, который может быть пропущен и вершины 1 в вершину 9, b) разрез, на котором максимальный поток равен его пропускной способности, c) найти разрез, на котором максимальный поток меньше его пропускной способности.
Варианты заданий приведены в следующей таблице:
Литература. 1. Моисеев Н.Н. Математические задачи системного анализа.–М., Наука, 1981, 487 с. 2. Гермейер Ю.Б. Введение в теорию исследования операций. – М., Наука, 1971. 3. Зайченко Ю.П. Исследование операций. – Киев, Вiща школа,1975. 4. Коваленко А.Г. Элементы выпуклого векторного программирования. Учебное пособие. – Самара, 1990, 83 стр. 5. Коваленко А.Г., Власова И.А. Цветков Ю.Д. – Лабораторный практикум по методам оптимизации. – Куйбышев, СамГУ, 1991, 59 стр. 6. Подиновский В.В., Ногин В.Д. Парето – оптимальные решения. М., Наука, 1971. 7. Дубов Ю.А. и др. Многокритериальные модели формирования и выбора вариантов систем. М., Наука, 1986. 8. Романовский И.В. Алгоритмы решения экстремальных задач. М. Наука, 1977. 9. Коваленко А.Г. Алгоритмы решения некоторых задач оптимизации многошаговых процессов. Куйбышев, 1985, 72 стр. 10.Тетерев А.Г. Динамическое программирование в курсе исследования операций. – Куйбышев, 1983. 11. Исследование операций под ред. Дж.Моудера, С.Элмаграби. М., "Мир",1981,т.1,2. 12. Корбут А.А., Финкельштейн Ю.Ю. Дискретное программирование. М. Наука М., Наука, 1971. 14. Хедли Дж. Нелинейное и динамическое программирование. – М., Мир, 1967. 15. Ху Т. Целочисленное программирование и потоки в сетях. М., Мир, 1971. 16. Танаев В.С., Шкурба В.В. Введение в теорию расписаний. М., Наука, 1975. 17. Беллман Р., Дрейфус С. Прикладные задачи динамического программирования. М., Мир, 1965. 18. Акоф Р., Сасиени М. Основы исследования операций. М. Мир. 1971. 19. Нейман Дж., Моргенштерн О. Теория игр и экономическое поведение. М., «Наука», 1970. 20. Подиновский В.В., Ногин В.Д. Парето–оптимальные решения многокритериальных задач. М. Наука, 1982, 256 с. 24.Коваленко А.Г., Власова И.А., Федечев А.Ф. Лабораторный практикум по методам оптимизации. Изд. «Самарский университет», Самара, 1998 г. 25.Коваленко А.Г., Власова И.А., Шведова И.А. Лабораторный практикум по методам исследования операций. Изд. «Самарский университет», Самара, 1997 г. 26. Юдин Д.Б., Гольштейн E. Г. Задачи линейного программирования транспортного типа. М. «Наука» 1969.
27. Бусыгин, В. П. Желободько Е. В., Коровин С. Г., Цыплаков А. А. Микроэкономический анализ несовершенных рынков: Ч.1.– Новосибирск: Новосибирский государственный университет, 2000. – 264 с. 28. Хачатуров, В. Р. Математические методы регионального программирования. – М.: Наука, 1989. – 304 с.
[1] В настоящей главе приведены основные теоремы векторного выпуклого программирования и многокритериальной задачи без доказательств, и авторы предлагают читателю самостоятельно доказать предложенные теоремы. Доказательства этих теорем можно найти в работах Коваленко А.Г. Элементы выпуклого векторного программирования [4] и Карманова В.Г. Математическое программирование [26].
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 707; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.009 с.) |

 или
или




 .
. .
. , на котором Q =
, на котором Q =  , будем называть ограничивающим. На ограничивающем разрезе выполняется
, будем называть ограничивающим. На ограничивающем разрезе выполняется
 .
. выполнить:
выполнить: выполнить:
выполнить: . Разрез
. Разрез  будет искомым.
будет искомым.

 . Поток поступил из вершины j = h 1(v 6)=2, переходим к анализу этой вершины.
. Поток поступил из вершины j = h 1(v 6)=2, переходим к анализу этой вершины. . Поток поступил из вершины j = h 2(v 4)=4, переходим к анализу этой вершины.
. Поток поступил из вершины j = h 2(v 4)=4, переходим к анализу этой вершины. . Поток поступил из вершины j = h 1(v 2)=1 – начальная вершина, цепь восстановления потока получена, изменения значений потоков вносим в таблицу
. Поток поступил из вершины j = h 1(v 2)=1 – начальная вершина, цепь восстановления потока получена, изменения значений потоков вносим в таблицу

 и поток по нему
и поток по нему  . Эти величины совпадают, на прямых дугах поток совпадает с ее пропускной способностью, на обратных дугах поток равен 0.
. Эти величины совпадают, на прямых дугах поток совпадает с ее пропускной способностью, на обратных дугах поток равен 0.

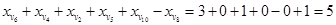 ,
,



